在庫を最適化せよ：Pythonによる数理最適化の威力

在庫管理は多くの企業にとって重要な課題です。

在庫が少なすぎれば機会損失、多すぎれば保管コストが膨らみます。

今回は、Pythonを使った数理最適化モデルを構築し、最適な在庫水準を決定する方法を解説します。

先ずは経済発注量（EOQ）モデルから始め、より複雑な確率的在庫モデル（モンテカルロシミュレーション）、そして安全在庫を考慮した多期間の在庫計画問題を扱います。

Contents

はじめに
経済発注量（EOQ）モデル
　問題設定
　Pythonによる実装
　結果の解釈と分析
確率的在庫モデル（s, S）政策
　問題設定
　Pythonによる実装
　結果の解釈と分析
多期間の在庫計画問題（数理最適化）
　問題設定
　最適化問題の定式化
　Pythonによる実装
　モデルの拡張と実務での活用
まとめ

はじめに

在庫管理は、多くの企業にとって収益性と効率性を大きく左右する重要な課題です。

適切な在庫水準を維持することで、品切れによる機会損失を防ぎつつ、過剰在庫による保管コストを抑えることができます。

しかし、需要の変動、リードタイムの不確実性、複数の商品カテゴリーなど、多くの変数と制約が絡み合う複雑な問題を、直感や経験だけで最適に解決するのは困難です。

ここで数理最適化の出番です。数理最適化とは、与えられた制約条件の下で目的関数を最大化（または最小化）する数学的手法です。

数理最適化の基本的な構成要素は以下の通りです。

決定変数：最適化によって決定したい未知の値（例：各期の発注量）
目的関数：最大化または最小化したい数式（例：総コストの最小化）
制約条件：問題に課される制限（例：倉庫の容量制限、最小在庫水準）

これらの要素を用いて在庫問題を数式化し、コンピュータの力を借りて最適解を求めます。

在庫最適化は、コスト削減、顧客満足度向上、そして持続可能な事業運営につながる重要な取り組みです。

経済発注量（EOQ）モデル

経済発注量（Economic Order Quantity, EOQ）モデルは、在庫管理の基本的なモデルです。

このモデルは、注文コストと保管コストのバランスを取りながら、最適な発注量を決定します。

　問題設定

以下のもとで、総コスト（注文コスト＋保管コスト）を最小化する最適な発注量を求めます。

年間需要 (D): 10,000個
1回の注文にかかる固定費用 (K): 100ドル
1個あたりの年間保管コスト (h): 2ドル
リードタイム: 一定（考慮しない）
品切れは許容されない

このときの決定変数は、以下です。

Q: 1回あたりの発注量

目的関数（年間総コスト）は、以下のようになります。最小化したいのは、この総コスト(TC)です。

\begin{array}{ll} \displaystyle TC & =\displaystyle\left({\small 年間の注文回数} \times {\small1回の注文コスト}\right) + \left({\small平均在庫} \times {\small単位あたりの保管コスト}\right)\\ & = \displaystyle \left(\frac{D}{Q} \times K\right) + \left(\frac{Q}{2} \times h\right) \end{array}

　Pythonによる実装

EOQモデルは解析的に解くことができますが、Pythonを使って数値的に解く方法も示します。

以下、コードです。

import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib 

# パラメータ
D = 10000  # 年間需要
K = 100    # 1回の注文にかかる固定費用
h = 2      # 1個あたりの年間保管コスト

# 総コスト関数
def total_cost(Q):
    return (D/Q * K) + (Q/2 * h)

# 最適なQを見つける
Q_values = np.linspace(100, 2000, 1000)
costs = [total_cost(Q) for Q in Q_values]
optimal_Q = Q_values[np.argmin(costs)]
optimal_cost = np.min(costs)

print(f"最適な発注量: {optimal_Q:.2f}")
print(f"最小総コスト: {optimal_cost:.2f}")

# グラフの描画
plt.figure(figsize=(10, 6))
plt.plot(Q_values, costs)
plt.plot(optimal_Q, optimal_cost, 'ro')  # 最適点を赤で表示
plt.xlabel('発注量 (Q)')
plt.ylabel('総コスト')
plt.title('EOQモデル：発注量と総コストの関係')
plt.grid(True)
plt.show()

以下、実行結果です。

最適な発注量: 999.60
最小総コスト: 2000.00

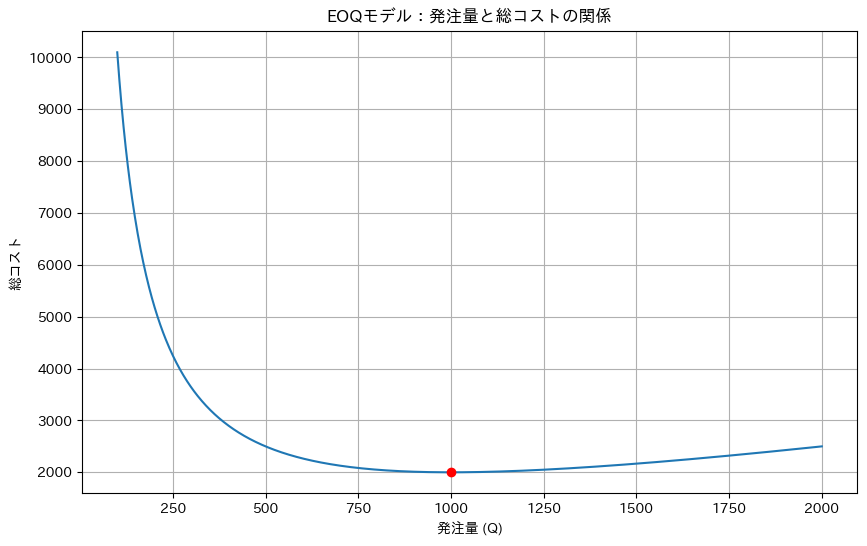
　結果の解釈と分析

この結果から、以下のような洞察が得られます。

最適な発注量は1,000個（四捨五入し整数値）です。これは、1回の注文で1,000個発注するのが最も経済的であることを意味します。
この最適発注量で運用した場合、年間の総コストは2,000ドルになります。
グラフを見ると、最適点の周りでは総コストの変化が緩やかであることがわかります。これは、厳密に1,000個でなくても、その付近の発注量であれば大きなコスト増にはならないことを示しています。
年間需要が10,000個なので、この最適発注量では年間10回の発注が必要になります。

EOQモデルは単純ですが、在庫管理の基本的な考え方を理解するのに役立ちます。

しかし、現実の在庫問題はより複雑です。次の章では、より現実的な要素を考慮した確率的在庫モデルを見ていきます。

確率的在庫モデル（s, S）政策

EOQモデルは単純で理解しやすいですが、現実の在庫問題には不確実性が伴います。

需要は変動し、リードタイムも一定とは限りません。不確実性を考慮した確率的在庫モデル、特に（s, S）政策について説明します。

　問題設定

先ほどの問題に、以下の要素を追加します。

日次需要は正規分布に従う（平均 40 個/日、標準偏差 10 個/日）
リードタイムは一様分布に従う（2〜5日の間）
品切れが発生した場合、1個あたり5ドルの機会損失が発生
在庫レベルは毎日終業時に確認される

その上で、長期的な総コスト（注文コスト＋保管コスト＋品切れコスト）を最小化する最適な $(s, S)$ 政策を求めます。

在庫レベルが s 以下になったら注文する
注文する際は、在庫レベルが S になるように注文する

このときの決定変数は、以下です。

s: 再発注点
S: 発注後の目標在庫レベル

目的関数（長期平均総コスト）は、以下のようになります。最小化したいのは、この総コスト(TC)です。

\displaystyle TC = \left(平均注文コスト\right) + \left(平均保管コスト\right) + \left(平均品切れコスト\right)

　Pythonによる実装

この問題は解析的に解くのが難しいため、シミュレーションを用いて最適な $(s, S)$ を求めます。

以下、コードです。難しそうに見えますが、単に仮定した確率分布に従いシミュレーションを実施しているだけです。

import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib 
from scipy.stats import norm, uniform

# パラメータ
D_mean = 40   # 日次需要の平均
D_std = 10    # 日次需要の標準偏差
LT_min = 2    # リードタイムの最小値
LT_max = 5    # リードタイムの最大値
K = 100       # 1回の注文にかかる固定費用
h = 0.1       # 1個あたりの日次保管コスト
p = 5         # 1個あたりの品切れコスト
days = 365    # シミュレーション日数


def simulate_inventory(s, S, num_simulations=100):
    total_costs = []
    
    for _ in range(num_simulations):
        inventory = S
        cost = 0
        pending_order = 0
        days_until_delivery = 0
        
        for _ in range(days):
            # 需要の生成
            demand = max(0, int(np.random.normal(D_mean, D_std)))
            
            # 在庫の更新
            if days_until_delivery == 0 and pending_order > 0:
                inventory += pending_order
                pending_order = 0
            
            if inventory < demand:
                # 品切れコスト
                cost += p * (demand - inventory)
                inventory = 0
            else:
                inventory -= demand
            
            # 保管コスト
            cost += h * inventory
            
            # 注文の確認
            if inventory <= s and pending_order == 0:
                cost += K
                pending_order = S - inventory
                days_until_delivery = int(uniform.rvs(LT_min, LT_max))
            
            if days_until_delivery > 0:
                days_until_delivery -= 1
        
        total_costs.append(cost)
    
    return np.mean(total_costs)

# グリッドサーチで最適な(s, S)を探索
s_values = range(50, 301, 10)
S_values = range(100, 501, 10)
results = []

for s in s_values:
    for S in S_values:
        if s < S:
            avg_cost = simulate_inventory(s, S)
            results.append((s, S, avg_cost))

optimal = min(results, key=lambda x: x[2])
print(f"最適な(s, S)政策: s={optimal[0]}, S={optimal[1]}")
print(f"最小平均コスト: {optimal[2]:.2f}")

# 結果の可視化
s_optimal, S_optimal = optimal[0], optimal[1]
costs = np.array([r[2] for r in results])
s_values_used = [r[0] for r in results]
S_values_used = [r[1] for r in results]

# ユニークなsとSの値を取得
unique_s = sorted(set(s_values_used))
unique_S = sorted(set(S_values_used))

# コストマップの作成
cost_map = np.full((len(unique_s), len(unique_S)), np.nan)
for i, (s, S, cost) in enumerate(results):
    s_index = unique_s.index(s)
    S_index = unique_S.index(S)
    cost_map[s_index, S_index] = cost

plt.figure(figsize=(10, 6))
plt.imshow(cost_map, cmap='viridis', aspect='auto', 
           extent=[min(unique_S), max(unique_S), max(unique_s), min(unique_s)])
plt.colorbar(label='平均総コスト')
plt.xlabel('S')
plt.ylabel('s')
plt.title('(s, S)政策のコストマップ')
plt.plot(S_optimal, s_optimal, 'r*', markersize=15)
plt.show()

このコードを実行すると、最適な $(s, S)$ 政策と対応する平均コストが得られます。

また、異なる $(s, S)$ の組み合わせに対するコストマップも出力しています。

以下、実行結果です。

最適な(s, S)政策: s=210, S=490
最小平均コスト: 12931.45

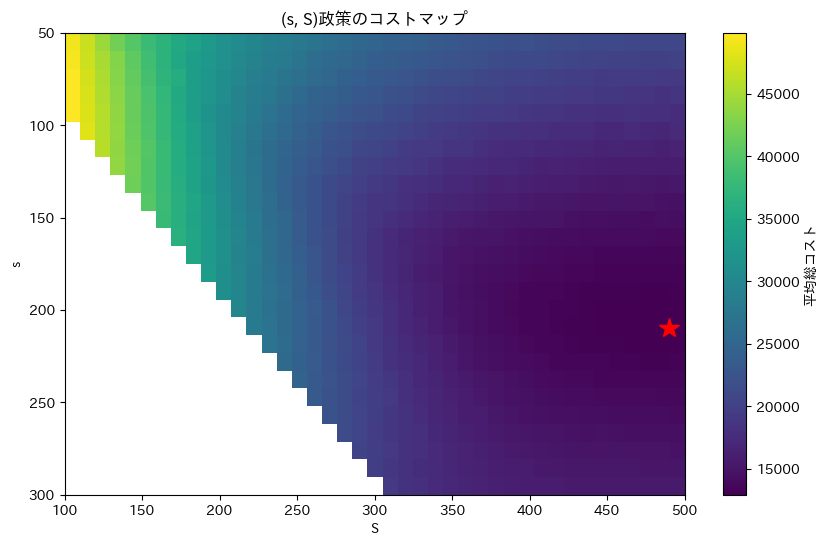
　結果の解釈と分析

この結果から、以下のような洞察が得られます。

発注点（s）が210個に設定されています。これは、在庫が210個以下になったら注文を出すべきことを意味します。
目標在庫レベル（S）は490個です。つまり、注文する際は490個まで在庫を補充します。
この政策で運用した場合、1年間の平均総コストは約12,931ドルと推定されます。
コストマップを見ると、最適点の周りでは比較的平坦な領域があることがわかります。これは、厳密に（s=210, S=490）でなくても、その付近の値であれば大きなコスト増にはならないことを示しています。
EOQモデルと比較すると、不確実性を考慮することで、より高い在庫水準が推奨されていることがわかります。これは、需要とリードタイムの変動に対するバッファーとして機能します。

このモデルは、現実の在庫管理により近い状況を表現しています。

需要の変動やリードタイムの不確実性を考慮することで、より堅牢な在庫政策を導き出すことができます。

多期間の在庫計画問題（数理最適化）

確率的な要素を考慮しつつ、線形計画法で解ける形に問題を定式化します。

ここでは、安全在庫を考慮した多期間の在庫計画問題を扱います。

　問題設定

以下の条件のもとで、総コスト（発注コスト + 在庫保管コスト + 在庫切れペナルティコスト）を最小化する問題を解きます。

計画期間: 6ヶ月（各月を1期間とする）
各期の予測需要は既知だが、不確実性がある
在庫切れは許容されるが、ペナルティコストが発生する
発注から納品まで1期間かかる（リードタイム1期間）
安全在庫を維持する必要がある

　最適化問題の定式化

以下、パラメータです。

$T$ : 計画期間の総数（6ヶ月）
$d_t$ : 期間 $t$ の予測需要
$K$ : 1回の発注にかかる固定費用
$c$ : 製品1単位あたりの仕入れ価格
$h$ : 製品1単位あたりの1期間の在庫保管コスト
$p$ : 製品1単位あたりの1期間の在庫切れペナルティコスト
$I_0$ : 初期在庫量
$SS$ : 安全在庫水準

以下、決定変数です。

$x_t$ : 期間 $t$ の発注量
$I_t$ : 期間 $t$ 終了時の在庫水準
$S_t$ : 期間 $t$ の在庫切れ量
$y_t$ : 期間 $t$ に発注するかどうかのバイナリ変数 (0 or 1)

記号が出揃ったところで、目的関数と制約条件を定義していきます。

目的関数（総コスト）

\displaystyle \sum_{t=1}^T (Ky_t + cx_t + hI_t + pS_t)

在庫バランス制約
$\displaystyle I_t = I_{t-1} + x_{t-1} - d_t + S_t, \quad \forall t \in \{1,...,T\}$

安全在庫制約
$\displaystyle I_t \geq SS, \quad \forall t \in \{1,...,T\}$

発注の有無を表す制約（ここで $M$ は十分大きな数）
$\displaystyle x_t \leq My_t, \quad \forall t \in \{1,...,T\}$

非負制約
$\displaystyle x_t, I_t, S_t \geq 0, \quad \forall t \in \{1,...,T\}$

バイナリ制約（0-1制約）
$\displaystyle y_t \in \{0,1\}, \quad \forall t \in \{1,...,T\}$

まとめると、以下のようになります。

\displaystyle\begin{array}{ll}\text{maximize} & \displaystyle \sum_{t=1}^T (Ky_t + cx_t + hI_t + pS_t) \\\text{subject to} & \displaystyle I_t = I_{t-1} + x_{t-1} - d_t + S_t, \quad \forall t \in \{1,...,T\} \\& \displaystyle I_t \geq SS, \quad \forall t \in \{1,...,T\} \\& \displaystyle x_t \leq My_t, \quad \forall t \in \{1,...,T\} \\& \displaystyle x_t, I_t, S_t \geq 0, \quad \forall t \in \{1,...,T\} \\& \displaystyle y_t \in \{0,1\}, \quad \forall t \in \{1,...,T\}\\\end{array}

　Pythonによる実装

PuLPというPythonライブラリを使用します。PuLPは直感的なインターフェースを持ち、線形計画問題を効率的に解くことができます。

このライブラリーは以下のコードでインストールできます。

pip install pulp

では、インストールされていることを前提に話しを進めます。

以下、コードです。

import pulp

# パラメータ設定
T = 6  # 計画期間
d = [100, 120, 80, 110, 90, 130]  # 各期の予測需要
K = 1000  # 発注固定費用
c = 10  # 単位あたりの仕入れ価格
h = 3  # 単位あたりの在庫保管コスト
p = 20  # 単位あたりの在庫切れペナルティコスト
I0 = 50  # 初期在庫
SS = 10  # 安全在庫水準

# モデルの作成
model = pulp.LpProblem("Inventory Optimization", pulp.LpMinimize)

# 決定変数の定義
x = {t: pulp.LpVariable(f"x_{t}", lowBound=0, cat='Integer') for t in range(T)}
I = {t: pulp.LpVariable(f"I_{t}", lowBound=0, cat='Integer') for t in range(T)}
S = {t: pulp.LpVariable(f"S_{t}", lowBound=0, cat='Integer') for t in range(T)}
y = {t: pulp.LpVariable(f"y_{t}", cat='Binary') for t in range(T)}

# 目的関数
model += pulp.lpSum(K * y[t] + c * x[t] + h * I[t] + p * S[t] for t in range(T))

# 制約条件
for t in range(T):
    if t == 0:
        model += I[t] == I0 + x[t] - d[t] + S[t]
    else:
        model += I[t] == I[t-1] + x[t-1] - d[t] + S[t]
    
    model += I[t] >= SS
    model += x[t] <= 1000 * y[t]  # M = 1000 (十分大きな数)

# モデルの解決
model.solve()

# 結果の表示
print(f"総コスト: {pulp.value(model.objective):.2f}")
print("\n期間ごとの結果:")
print("期 発注量 在庫水準 在庫切れ量")
for t in range(T):
    print(f"{t+1:2d} {x[t].value():7.0f} {I[t].value():8.0f} {S[t].value():10.0f}")

このコードを実行すると、最適な発注計画と各期の在庫水準が得られます。

発注パターン：どの期間で発注が行われ、その量はどれくらいか
在庫水準の推移：安全在庫水準がどのように維持されているか
在庫切れの発生：在庫切れが発生する期間とその量
コスト構造：総コストに占める各コスト要素（発注、保管、ペナルティ）の割合

以下、実行結果です。

総コスト: 7895.00

期間ごとの結果:
期 発注量 在庫水準 在庫切れ量
 1     185      135          0
 2       0      200          0
 3       0      120          0
 4     220       10          0
 5       0      140          0
 6       0       10          0