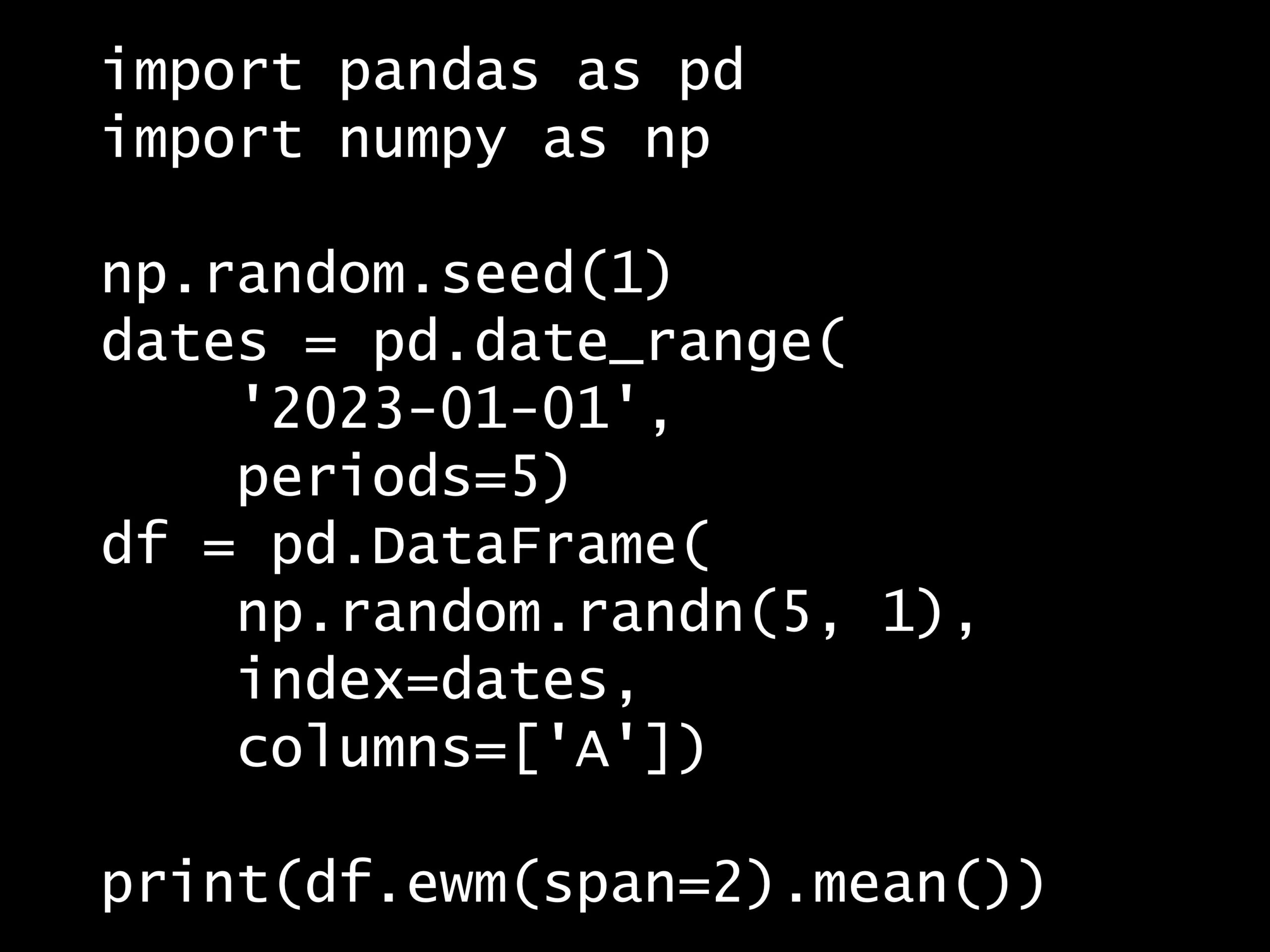
Python 時系列分析 1,000本ノック– ノック11: 時系列データの平滑化 –

次の Python コードの出力はどれでしょうか？

Python コード:

import pandas as pd
import numpy as np

np.random.seed(1)
dates = pd.date_range('2023-01-01', periods=5)
df = pd.DataFrame(
    np.random.randn(5, 1), 
    index=dates, 
    columns=['A'])

print(df.ewm(span=2).mean())

回答の選択肢:

A. 連続する値のランダムな平均
B. 指数加重移動平均に基づく滑らかな値
C. 全ての値が0に近い
D. データが単調に増加または減少

出力例:

                   A
2023-01-01  1.624345
2023-01-02 -0.052731
2023-01-03 -0.381882
2023-01-04 -0.848366
2023-01-05  0.298871

正解:

解説:

このコードは、標準正規分布からランダムな値を生成しデータフレームdfを作成します。

dfに格納されているデータは次のようになっています。ランダムな値を入れているため、人によって値は異なります。

                   A
2023-01-01  1.624345
2023-01-02 -0.611756
2023-01-03 -0.528172
2023-01-04 -1.072969
2023-01-05  0.865408

データフレームdfに対しewm(span=2).mean() メソッドを使うことで、指数加重移動平均（Exponentially Weighted Moving Average、EWMA）を計算します。この方法は、より最近のデータに重みを大きくし、古いデータには重みを小さくすることで、時系列データを平滑化します。span=2 は減衰因子を設定し、この値が小さいほど最近の観測値に大きな重みが与えられます。結果として、データはより滑らかな形で表現され、各日付の値は前の値に依存します。

ちなみに、指数加重移動平均は、時系列データを平滑化するための手法の一つで、最新のデータにより高い重みを与え古いデータには徐々に低い重みを与えるような移動平均を計算します。