Python 時系列分析 1,000本ノック– ノック38: 季節性トレンド分解 –

問題
答え
解説
季節性トレンド分解 seasonal_decompose 関数

次の Python コードの出力はどれでしょうか？

Python コード:

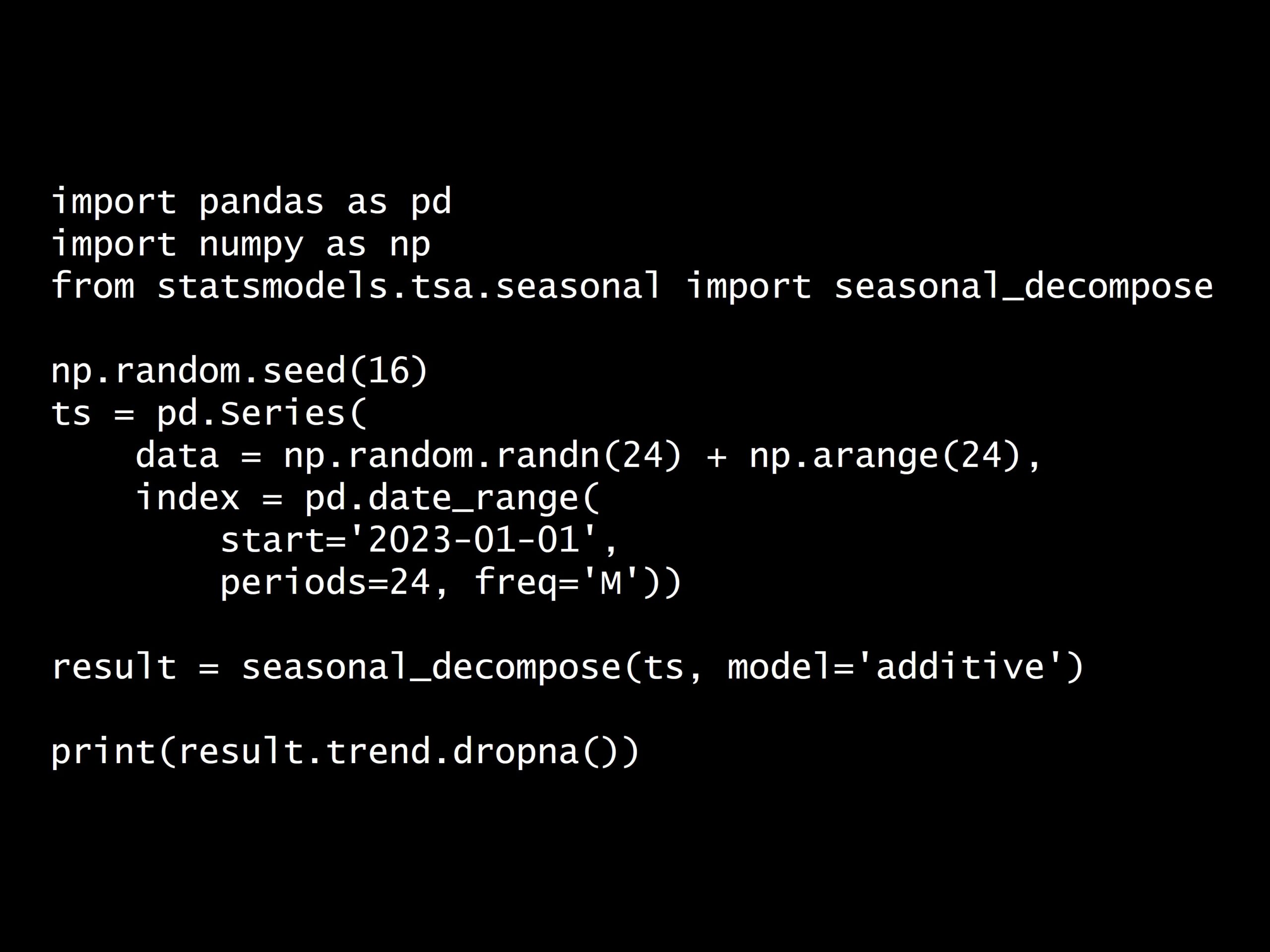
import pandas as pd
import numpy as np
from statsmodels.tsa.seasonal import seasonal_decompose

np.random.seed(16)
ts = pd.Series(
    data = np.random.randn(24) + np.arange(24), 
    index = pd.date_range(
        start='2023-01-01', 
        periods=24, freq='M'))

result = seasonal_decompose(ts, model='additive')

print(result.trend.dropna())

回答の選択肢:

(A) 時系列データから季節性成分を引いた値
(B) 時系列データから季節性成分とノイズを引いた値
(C) 時系列データを季節性成分とノイズで割った値
(D) 時系列データを季節性成分で割った後にノイズを引いた値

出力例:

2023-07-31     5.534092
2023-08-31     6.515180
2023-09-30     7.547072
2023-10-31     8.633325
2023-11-30     9.749271
2023-12-31    10.754864
2024-01-31    11.712299
2024-02-29    12.790423
2024-03-31    13.900124
2024-04-30    14.915063
2024-05-31    15.949441
2024-06-30    17.039111
Freq: M, Name: trend, dtype: float64

正解: (B)

回答の選択肢:

このコードは、時系列データに対して季節性トレンド分解をしています。季節性トレンド分解は、時系列データをいくつかの成分(トレンド、季節性、誤差)に分ける分析手法です。

import pandas as pd
import numpy as np
from statsmodels.tsa.seasonal import seasonal_decompose

np.random.seed(16)
ts = pd.Series(
    data = np.random.randn(24) + np.arange(24), 
    index = pd.date_range(
        start='2023-01-01', 
        periods=24, freq='M'))

result = seasonal_decompose(ts, model='additive')

print(result.trend.dropna())

詳しく説明します。

statsmodels.tsa.seasonalからseasonal_decomposeをインポートします。これで、季節性トレンド分解を行います。

from statsmodels.tsa.seasonal import seasonal_decompose

numpyの乱数生成機能を用いて、ランダムノイズを含む時系列データを作成します。

ts = pd.Series(
    data = np.random.randn(24) + np.arange(24), 
    index = pd.date_range(
        start='2023-01-01', 
        periods=24, freq='M'))

データは正規分布からランダムに選ばれ（`np.random.randn(24)`）、これに 0 から 23までの整数の順列（`np.arange(24)`）を足すことで、一定のトレンドを持つ時系列データを生成します。

インデックスとして’2023-01-01’から始まる月末の日付を24個作成します（`pd.date_range(start=’2023-01-01′, periods=24, freq=’M’)`）。

tsに格納されているデータは次のようになっています。

2023-01-31     0.127949
2023-02-28    -0.528473
2023-03-31     1.405532
2023-04-30     3.066330
2023-05-31     2.764505
2023-06-30     4.378631
2023-07-31     5.111052
2023-08-31     7.498910
2023-09-30     7.213103
2023-10-31     9.118744
2023-11-30     9.243137
2023-12-31    11.493367
2024-01-31    11.160596
2024-02-29    11.984978
2024-03-31    13.657480
2024-04-30    16.884464
2024-05-31    15.729087
2024-06-30    15.548281
2024-07-31    16.919841
2024-08-31    21.565077
2024-09-30    19.779777
2024-10-31    20.910600
2024-11-30    22.276341
2024-12-31    24.612261
Freq: M, dtype: float64

時系列データtsに対し、季節性トレンド分解を行い(`seasonal_decompose(ts, model=’additive’)`)、その結果をresultに格納します。今回は、時系列データがトレンド、季節性、そしてノイズの和としてモデル化される加法モデル（additive）としています。

result = seasonal_decompose(ts, model='additive')

resultのトレンド成分（result.trend）を出力します。トレンド成分にはNaN（欠損値）が含まれるため削除（dropna()）した後に出力しています。

print(result.trend.dropna())

2023-07-31     5.534092
2023-08-31     6.515180
2023-09-30     7.547072
2023-10-31     8.633325
2023-11-30     9.749271
2023-12-31    10.754864
2024-01-31    11.712299
2024-02-29    12.790423
2024-03-31    13.900124
2024-04-30    14.915063
2024-05-31    15.949441
2024-06-30    17.039111
Freq: M, Name: trend, dtype: float64

加法モデル（additive）では、時系列データがトレンド、季節性、そしてノイズの和としてモデル化されます。そのため、加法モデル（additive）のトレンド成分は「時系列データから季節性成分とノイズを引いた値」です。

ちなみに、以下は季節性トレンド分解の結果であるresultオブジェクトの主な属性やメソッドです。

observed：元の時系列データです。
trend：時系列データから季節性と残差成分を除くと得られる、データのトレンドです。
seasonal：時系列データから周期的なパターン（季節性）を表します。
resid：時系列データからトレンドと季節性を除いた後の残余（あるいは誤差）です。
plot：分解した結果をグラフ化するためのメソッドです。これを使用すると、元のデータ、トレンド、季節性、残差の4つのプロットを一つの図に表示できます。
weights：季節性分解のための加重です。これは基本的に季節性分解のモデルが乗法である場合に使用され、各観測値に対する加重を持っています。

statsmodels.tsa.seasonal の seasonal_decompose 関数は、Pythonの統計モデリングライブラリである statsmodels の一部です。この関数は、時系列データを分析する際に使用され、主に3つの成分に分解します。

トレンド（Trend）: これはデータの長期的な上昇または下降傾向を指します。トレンド成分は、時間の経過に伴うデータの変動を反映し、周期的ではない傾向を表します。
季節性（Seasonality）: 季節性成分は、定期的なパターンや周期を表します。これは、日、週、月、四半期、年などの周期に沿ったデータの変動を捉えます。たとえば、小売業の場合、クリスマスシーズンの売上が毎年増加するのは一般的な季節的パターンです。
残差（Residual）: 残差成分は、トレンドや季節性によって説明されないデータの部分を表します。これはノイズやデータのランダムな変動を捉えるもので、分析の際にはしばしば重要な情報を含んでいます。

seasonal_decompose 関数の使用方法は以下の通りです。

from statsmodels.tsa.seasonal import seasonal_decompose

# 時系列データを読み込む
# 例: pandas DataFrameを使用
timeseries_data = ...

# 季節性トレンド分解実施
decomposition = seasonal_decompose(
     timeseries_data, 
     model='additive', 
     period=...)

# 成分を分解する
trend = decomposition.trend #トレンド成分
seasonal = decomposition.seasonal #季節成分
residual = decomposition.resid #残差

ここで、model パラメーターは、分解を加算モデル（’additive’）または乗算モデル（’multiplicative’）のどちらかで行うかを指定します。

加算モデルはデータの変動が一定である場合に適しており、乗算モデルは変動が比例して増加または減少する場合に適しています。period パラメーターはデータの季節性の期間を指定します（例：月間データでは12、週間データでは52など）。

加算モデル（’additive’）と乗算モデル（’multiplicative’）は、時系列データの分析において重要な概念です。これらは、データのトレンド、季節性、そして残差成分をモデル化する方法を定義します。これらのモデルの選択は、データの特性に大きく依存します。

加算モデル（Additive Model）

加算モデルでは、時系列データはトレンド、季節性、残差の和として表されます。数式で表すと、以下のようになります。