次の Python コードの出力はどれでしょうか？

Python コード:

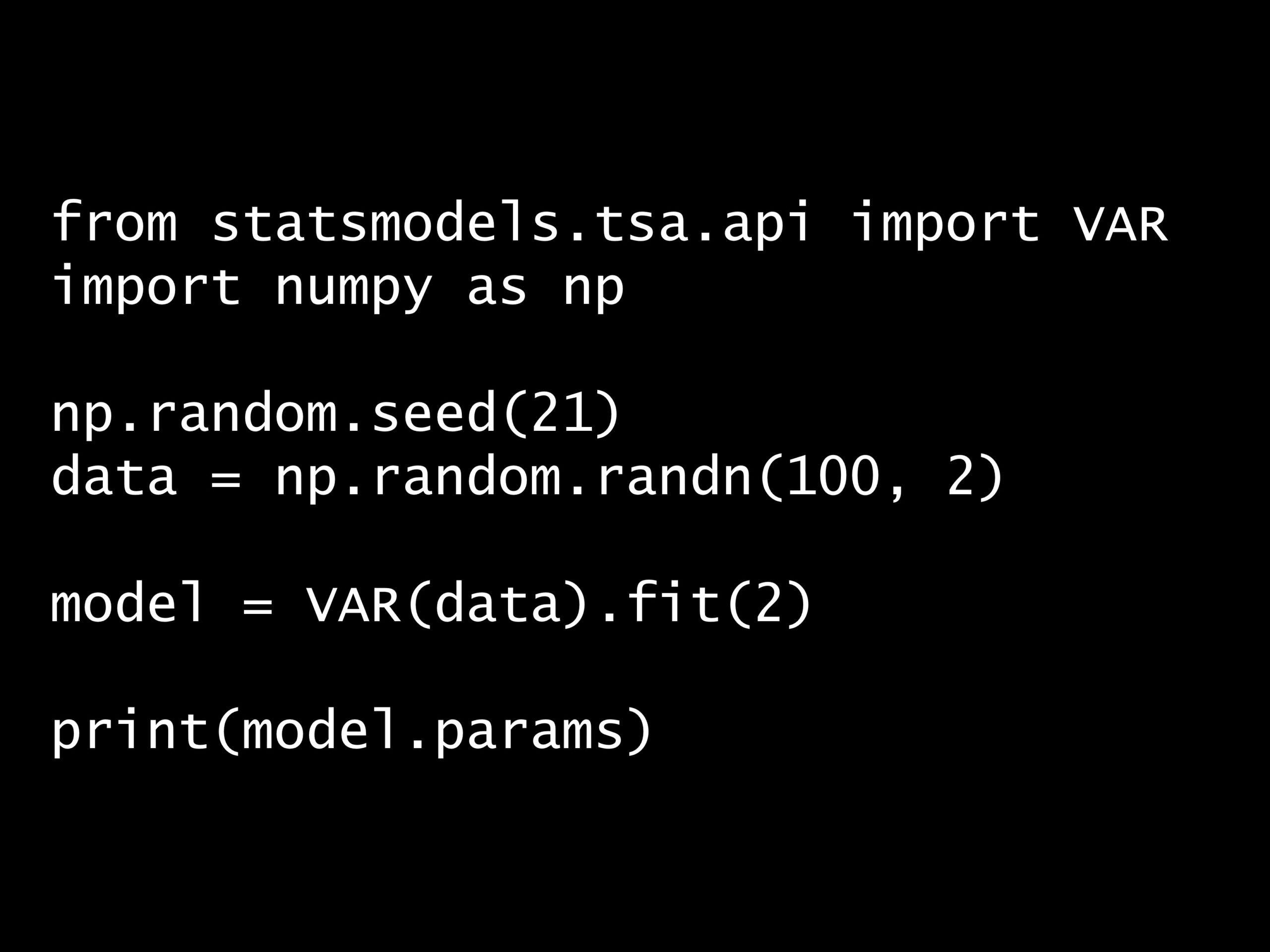
from statsmodels.tsa.api import VAR
import numpy as np

np.random.seed(21)
data = np.random.randn(100, 2)

model = VAR(data).fit(2)

print(model.params)

 

回答の選択肢:

(A) VARモデルの引数
(B) VARモデルの係数
(C) VARモデルの媒介変数
(D) VARモデルの予測値

出力例:

[[-0.15624661  0.1255323 ]
 [-0.02258053 -0.13647131]
 [ 0.11729959  0.06194475]
 [ 0.09764951 -0.03533967]
 [ 0.1638414  -0.15434321]]

 

正解: (B)
 

回答の選択肢:

(A) VARモデルの引数
(B) VARモデルの係数
(C) VARモデルの媒介変数
(D) VARモデルの予測値

このPythonコードは、VAR（Vector Autoregression）モデルを用いた時系列解析の例を示しています。

from statsmodels.tsa.api import VAR
import numpy as np

np.random.seed(21)
data = np.random.randn(100, 2)

model = VAR(data).fit(2)

print(model.params)

 

詳しく説明します。

numpyの乱数生成器を用いて2次元のランダムデータdataを生成しています。

np.random.seed(21)
data = np.random.randn(100, 2)

 

dataに格納されているデータは次のようになっています。

[[-0.05196425 -0.11119605]
 [ 1.0417968  -1.25673929]
 [ 0.74538768 -1.71105376]
 [-0.20586438 -0.23457129]
 [ 1.12814404 -0.01262595]
 [-0.61320029  1.3736885 ]
 [ 1.61099198 -0.68922827]
 [ 0.69192371 -0.4481156 ]
 [ 0.16234247  0.25722913]
 [-1.27545586  0.06400443]
 [-1.06185662 -0.98936839]
 [-0.45772323 -1.98418161]
 [-1.47644212  0.23180296]
 [ 0.64415927  0.8521227 ]
 [-0.46401872  0.6971766 ]
 [ 1.56788218  1.17855621]
 [-1.38395687 -1.7473338 ]
 [ 0.40272379  1.2444828 ]
 [-0.02383635  0.95256771]
 [ 0.24496394  0.22409714]
 [ 0.2966812   0.22075339]
 [-0.42330083  1.84561511]
 [ 0.92011457 -0.55791623]
 [-0.28522504 -1.04126664]
 [ 0.48036943 -1.4273776 ]
 [-0.33326642  0.74730849]
 [ 0.56022963  0.57370894]
 [-1.18088052  0.76465008]
 [-0.13438498  1.32463768]
 [-0.27642765  1.67955097]
 [ 0.41516187  0.7476816 ]
 [-0.39253041 -0.40632407]
 [-0.38584597  1.00090218]
 [-0.44768243 -0.11608402]
 [ 1.16901462  0.51561395]
 [-0.25786723  0.28504581]
 [-1.40459035 -1.50908235]
 [ 0.43430789  2.7550033 ]
 [ 2.01079281  2.51989837]
 [ 0.57043758 -0.52651551]
 [ 1.06822315 -1.19454337]
 [-2.85968799  0.42420703]
 [ 1.03361263  0.70520358]
 [ 1.55026502  0.76541945]
 [ 0.34630878 -1.05381731]
 [-0.12948877 -1.18143446]
 [-0.36883019  1.90273993]
 [ 0.21020722  0.37670281]
 [-0.6939358   2.60281328]
 [-1.98327783 -0.92686366]
 [ 0.94589607 -0.75058415]
 [-0.79426004  0.50839833]
 [ 0.74840916  0.68263421]
 [-0.85617032  0.75327818]
 [-1.209775   -0.91753224]
 [-0.9968251   0.32769691]
 [-0.35221334 -0.95180186]
 [ 0.03149344 -1.02345279]
 [-0.50486226 -0.31190012]
 [-0.56788809 -1.00610927]
 [-1.24792045  1.09858952]
 [-2.067628    0.29788031]
 [-0.80506766 -0.7078166 ]
 [-1.78303402 -0.03054955]
 [-0.55480147  1.0589691 ]
 [-0.56581211 -1.08983911]
 [-1.20112919  0.95681293]
 [ 0.56789824 -0.34917177]
 [ 1.65886138  0.26628553]
 [-0.29433165  0.5179977 ]
 [-1.10112241  0.10037062]
 [-1.13225522  0.57577806]
 [ 0.63296768 -0.1093355 ]
 [ 1.07672883 -0.70296868]
 [ 0.53877998 -0.12449926]
 [-1.15486369  0.68791271]
 [ 1.69837679  3.09448155]
 [ 0.09240797  0.48079649]
 [ 1.70883616 -1.04965817]
 [ 1.51663477 -1.66061318]
 [-1.15565445 -0.22414226]
 [-0.38386674  0.96739201]
 [-1.06796141 -0.12656273]
 [-0.34899674  0.16285447]
 [ 0.61363004  0.93287872]
 [ 0.32108345  0.38325003]
 [ 0.05004904 -1.56208124]
 [-1.82655664  0.35921196]
 [-1.38755461 -0.78991154]
 [ 0.21875741 -0.35145968]
 [-0.79893047 -0.90331589]
 [ 0.03740546  1.46745957]
 [-1.69777502 -0.24568898]
 [ 0.96158497  0.26374839]
 [-0.59817609  0.03230436]
 [ 0.40891293  1.01603581]
 [-1.59830998 -0.86143965]
 [ 0.27633421  0.43336544]
 [ 0.24397505  0.41139831]
 [ 0.88277695  0.45908868]]

 

この生成されたデータdataに対して、VARモデルを適用します。

VARモデルの`.fit()`メソッドを用いてモデルのパラメータ（係数など）をデータから推定します。ここでは引数に`2`を指定しており、これはモデルに2つのラグ（過去のデータをどの程度まで見るか）を考慮させることを意味します。

model = VAR(data).fit(2)

 

VARモデルのパラメーター（係数）を出力します。

print(model.params)

[[-0.15624661  0.1255323 ]
 [-0.02258053 -0.13647131]
 [ 0.11729959  0.06194475]
 [ 0.09764951 -0.03533967]
 [ 0.1638414  -0.15434321]]

このパラメーターは、それぞれの時系列データが過去の自身の値と他の時系列データの過去の値をどの程度考慮するかを示しています。これにより、各時系列データがどのように他のデータに影響を及ぼしているかを解析することができます。
 

modelオブジェクトは、statsmodelsライブラリのVARクラスによって生成され、フィットされたVARモデル（ベクトル自己回帰モデル）を表しています。

以下は、modelオブジェクトの主要な属性とメソッドです。

• params：モデルのパラメータ（係数）を格納するために用いられます。これらは、モデルを適合させる時にデータから推定されます。
• rss：残差平方和（RSS）を返します。これはモデルの適合度を評価するのに一般的に使用される指標です。
• k_ar：モデルが考慮するラグの数を返します。
• nobs：モデルの適合に使用された観測値の数を返します。
• forecast(y, steps)：与えられたyの値を起点として、stepsステップ分の未来の値を予測します。
• plot()：モデルの各コンポーネントのプロットを作成します。
• summary()：モデルの要約統計量をテーブル形式で提供します。

このような属性やメソッドを使うことで、フィットされたVARモデルの詳細な情報を取得したり、新しいデータに対して予測を行ったりすることができます。

VAR（Vector Autoregression）モデルは、複数の時系列データの相互関係をモデリングするための統計的手法で、自身の過去の値と他の時系列データの過去の値の線形結合としてモデリングされます。

p次のVARモデルは以下の形で表されます。

\displaystyle y_t = c + A_1 \times y_{t-1} + A_2 \times y_{t-2} + \cdots + A_p \times y_{t-p} + e_t

ここで、

• y_t は時点tにおけるm次元の時系列ベクトル
• c はm次元の定数ベクトル
• A_1, A_2, \cdots , A_p はm \times m次元の行列（各Aは各時系列の過去の値が現在の値にどのように影響を及ぼすかを表す）
• e_t は時点tにおけるm次元の誤差項またはノイズベクトル
• pはモデルの次数またはラグの数

それぞれの時系列データは、自身の過去のp個の値と、他の時間系列データの過去のp個の値によって説明されます。こういった構造が多変量時系列データの相互依存関係をモデリングすることを可能にします。

これらすべての互いの影響を一度に捉えるために、VARモデルを用いて複数の時系列データを一元的に分析することができます。これにより、各経済指標がどのように他の指標に影響を及ぼしているかを推定することが可能となります。

また、VARモデルは予測を行うためにも使用されます。複数の時系列データに基づいてVARモデルを適合させることにより、未来のデータポイントを予測することが可能となります。これは、金融市場分析や気候予測など、様々な分野で利用されています。