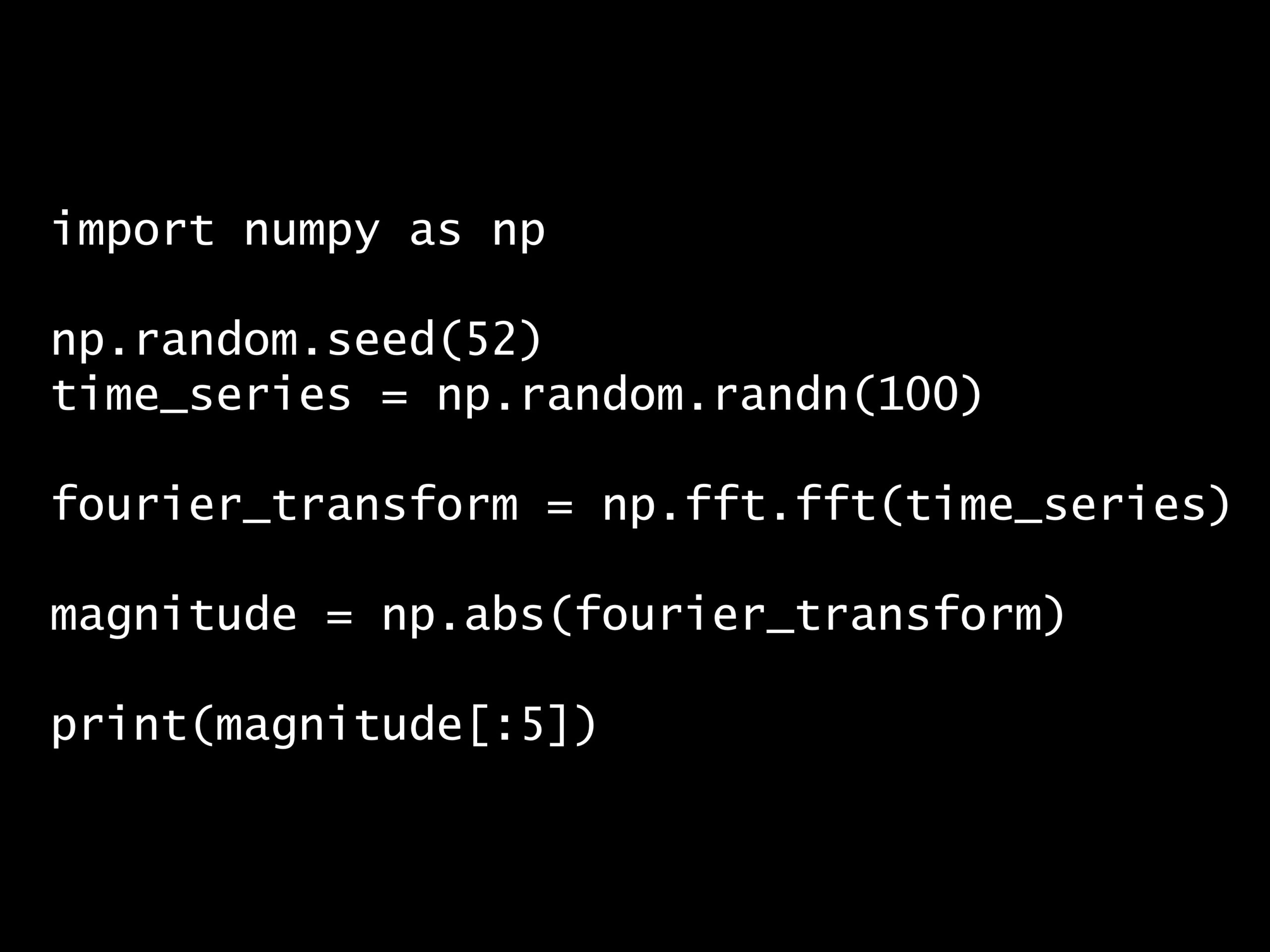
Python 時系列分析 1,000本ノック
– ノック48: フーリエ変換 –

1132
Python 時系列分析 1,000本ノック– ノック48: フーリエ変換 –
次の Python コードの出力はどれでしょうか？

Python コード:

Plain text
Copy to clipboard
Open code in new window
EnlighterJS 3 Syntax Highlighter
import numpy as np
np.random.seed(52)
time_series = np.random.randn(100)
fourier_transform = np.fft.fft(time_series)
magnitude = np.abs(fourier_transform)
print(magnitude[:5])
import numpy as np np.random.seed(52) time_series = np.random.randn(100) fourier_transform = np.fft.fft(time_series) magnitude = np.abs(fourier_transform) print(magnitude[:5])
import numpy as np

np.random.seed(52)
time_series = np.random.randn(100)

fourier_transform = np.fft.fft(time_series)

magnitude = np.abs(fourier_transform)

print(magnitude[:5])

 

回答の選択肢:

(A) フーリエ変換後の最初の5つの振幅
(B) フーリエ変換後の最初の5つのパワー
(C) フーリエ変換後の最初の5つの位相
(D) フーリエ変換後の最初の5つの周波数