- 問題
- 答え
- 解説
次の Python コードの出力はどれでしょうか?
Python コード:
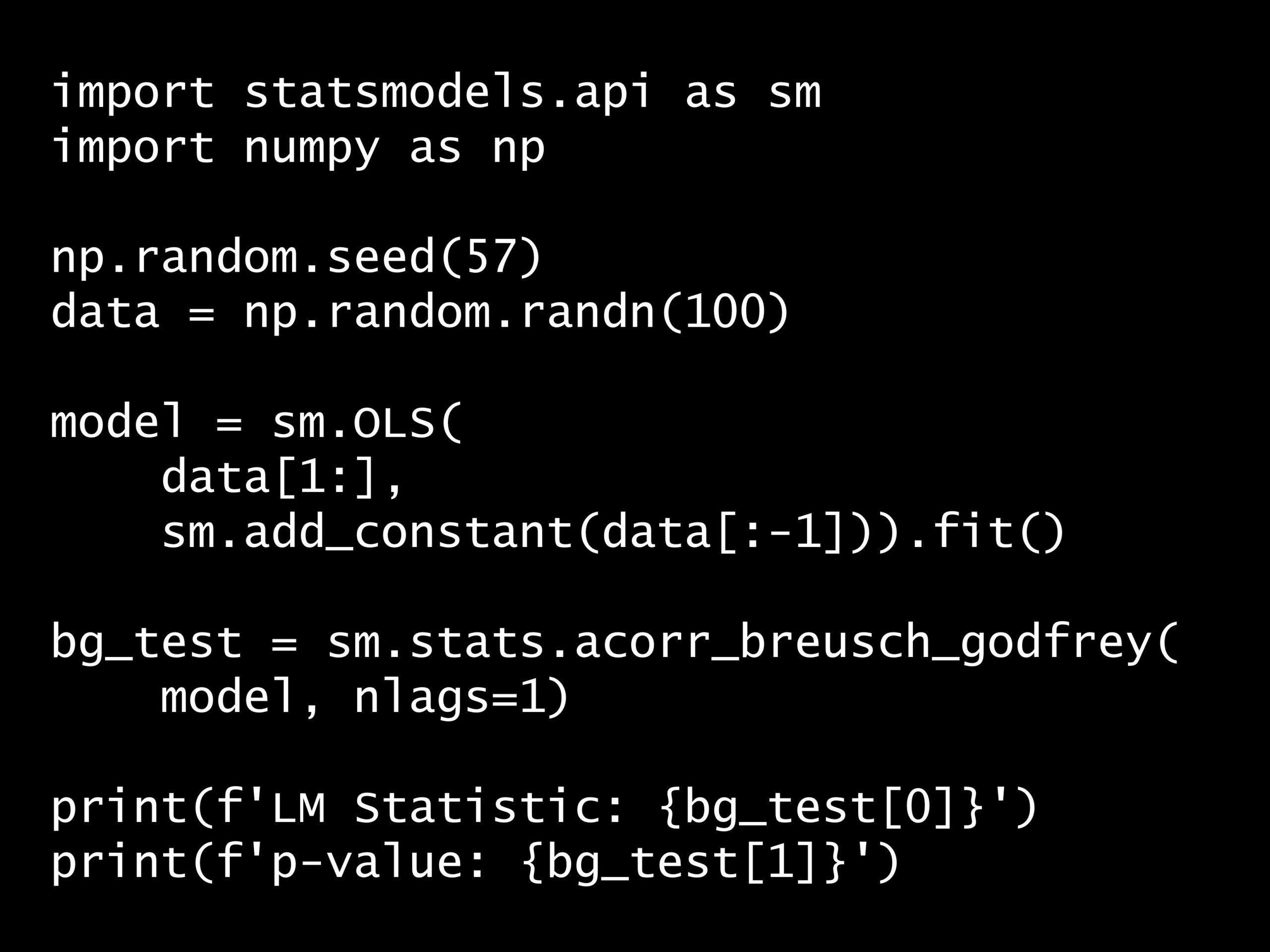
import statsmodels.api as sm
import numpy as np
np.random.seed(57)
data = np.random.randn(100)
model = sm.OLS(
data[1:],
sm.add_constant(data[:-1])).fit()
bg_test = sm.stats.acorr_breusch_godfrey(
model, nlags=1)
print(f'LM Statistic: {bg_test[0]}')
print(f'p-value: {bg_test[1]}')
import statsmodels.api as sm
import numpy as np
np.random.seed(57)
data = np.random.randn(100)
model = sm.OLS(
data[1:],
sm.add_constant(data[:-1])).fit()
bg_test = sm.stats.acorr_breusch_godfrey(
model, nlags=1)
print(f'LM Statistic: {bg_test[0]}')
print(f'p-value: {bg_test[1]}')
import statsmodels.api as sm
import numpy as np
np.random.seed(57)
data = np.random.randn(100)
model = sm.OLS(
data[1:],
sm.add_constant(data[:-1])).fit()
bg_test = sm.stats.acorr_breusch_godfrey(
model, nlags=1)
print(f'LM Statistic: {bg_test[0]}')
print(f'p-value: {bg_test[1]}')
回答の選択肢:
(A) 残差に自己相関が存在するかを検定する
(B) 定常性を持つかを検定する
(C) 共和分関係が存在するかを検定する
(D) 季節成分を検出する