- 問題
- 答え
- 解説
次の Python コードの出力はどれでしょうか?
Python コード:
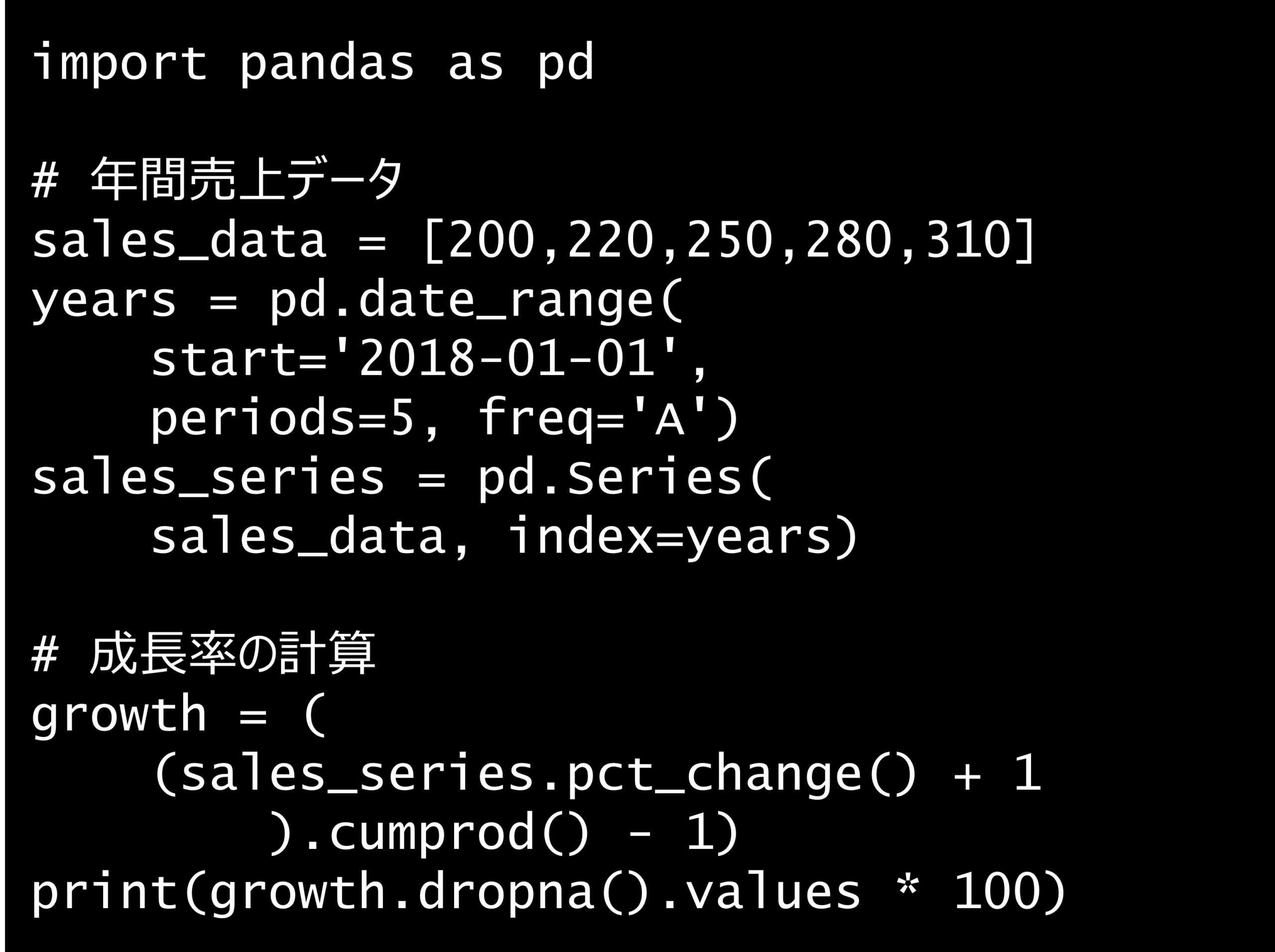
import pandas as pd
# 年間売上データ
sales_data = [200,220,250,280,310]
years = pd.date_range(
start='2018-01-01',
periods=5, freq='A')
sales_series = pd.Series(
sales_data, index=years)
# 成長率の計算
growth = (
(sales_series.pct_change() + 1
).cumprod() - 1)
print(growth.dropna().values * 100)
import pandas as pd
# 年間売上データ
sales_data = [200,220,250,280,310]
years = pd.date_range(
start='2018-01-01',
periods=5, freq='A')
sales_series = pd.Series(
sales_data, index=years)
# 成長率の計算
growth = (
(sales_series.pct_change() + 1
).cumprod() - 1)
print(growth.dropna().values * 100)
import pandas as pd
# 年間売上データ
sales_data = [200,220,250,280,310]
years = pd.date_range(
start='2018-01-01',
periods=5, freq='A')
sales_series = pd.Series(
sales_data, index=years)
# 成長率の計算
growth = (
(sales_series.pct_change() + 1
).cumprod() - 1)
print(growth.dropna().values * 100)
回答の選択肢:
(A) [1.10 1.25 1.40 1.55]
(B) [1.10 1.14 1.12 1.11]
(C) [10.0 13.6 12.0 10.7]
(D) [10.0 25.0 40.0 55.0]