- 問題
- 答え
- 解説
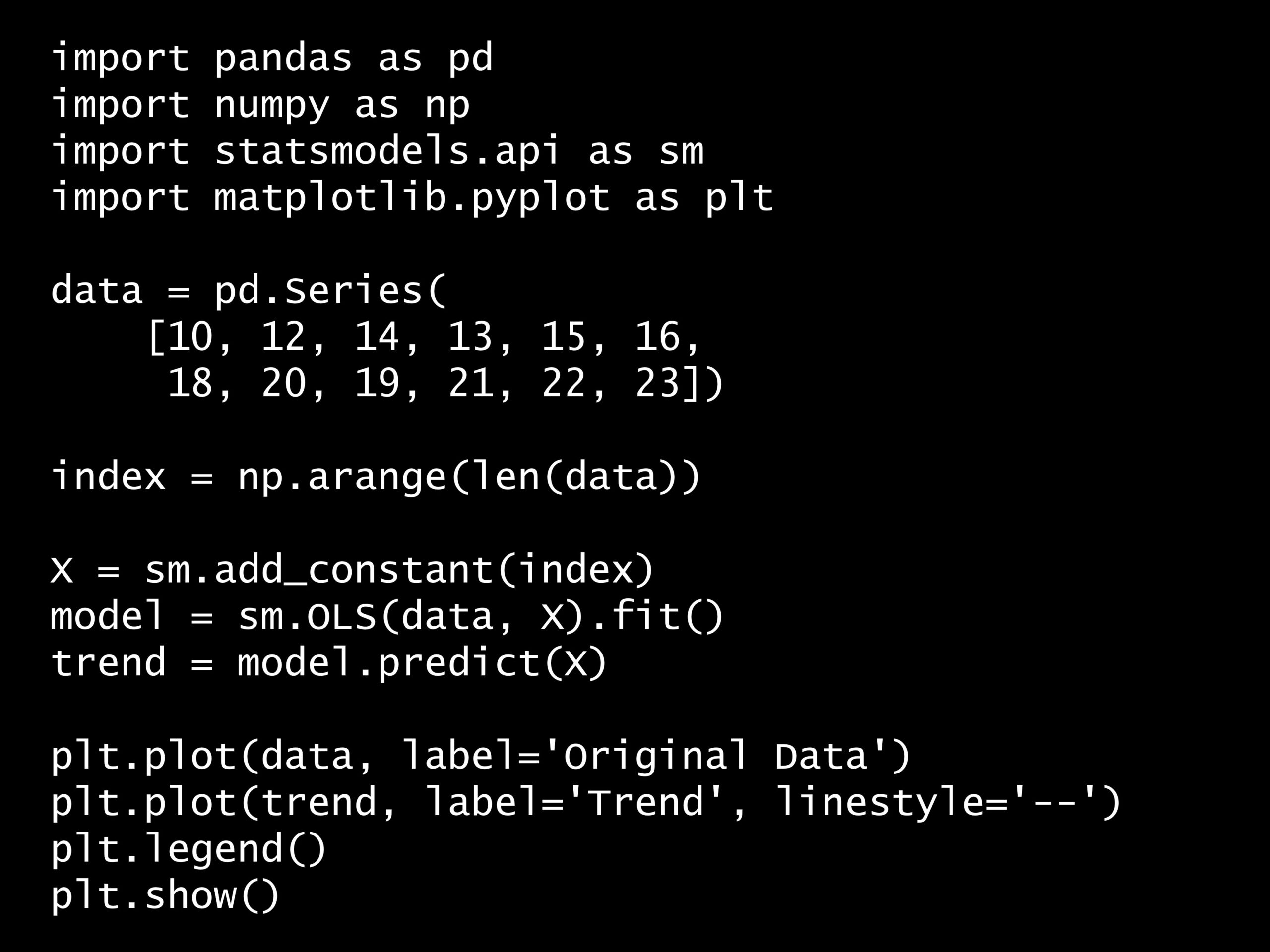
Python コード:
import pandas as pd
import numpy as np
import statsmodels.api as sm
import matplotlib.pyplot as plt
# 日次データの生成
data = pd.Series(
[10, 12, 14, 13, 15, 16,
18, 20, 19, 21, 22, 23])
# インデックスを取得
index = np.arange(len(data))
# トレンド推定
X = sm.add_constant(index)
model = sm.OLS(data, X).fit()
trend = model.predict(X)
plt.plot(data, label='Original Data')
plt.plot(trend, label='Trend', linestyle='--')
plt.legend()
plt.show()
回答の選択肢:
(A) Hodrick-Prescottフィルターによるトレンド推定
(B) 移動平均によるトレンド推定
(C) 最小二乗法回帰によるトレンド推定
(D) Fourier変換によるトレンド推定
正解: (C)
回答の選択肢:
(A) Hodrick-Prescottフィルターによるトレンド推定
(B) 移動平均によるトレンド推定
(C) 最小二乗法回帰によるトレンド推定
(D) Fourier変換によるトレンド推定
- コードの解説
-
このコードは、時系列データの自己相関を可視化するためのものです。Plain textCopy to clipboardOpen code in new windowEnlighterJS 3 Syntax Highlighterimport pandas as pdimport numpy as npimport statsmodels.api as smimport matplotlib.pyplot as plt# 日次データの生成data = pd.Series([10, 12, 14, 13, 15, 16,18, 20, 19, 21, 22, 23])# インデックスを取得index = np.arange(len(data))# トレンド推定X = sm.add_constant(index)model = sm.OLS(data, X).fit()trend = model.predict(X)plt.plot(data, label='Original Data')plt.plot(trend, label='Trend', linestyle='--')plt.legend()plt.show()import pandas as pd import numpy as np import statsmodels.api as sm import matplotlib.pyplot as plt # 日次データの生成 data = pd.Series( [10, 12, 14, 13, 15, 16, 18, 20, 19, 21, 22, 23]) # インデックスを取得 index = np.arange(len(data)) # トレンド推定 X = sm.add_constant(index) model = sm.OLS(data, X).fit() trend = model.predict(X) plt.plot(data, label='Original Data') plt.plot(trend, label='Trend', linestyle='--') plt.legend() plt.show()
import pandas as pd import numpy as np import statsmodels.api as sm import matplotlib.pyplot as plt # 日次データの生成 data = pd.Series( [10, 12, 14, 13, 15, 16, 18, 20, 19, 21, 22, 23]) # インデックスを取得 index = np.arange(len(data)) # トレンド推定 X = sm.add_constant(index) model = sm.OLS(data, X).fit() trend = model.predict(X) plt.plot(data, label='Original Data') plt.plot(trend, label='Trend', linestyle='--') plt.legend() plt.show()詳しく説明します。
日次データの生成し
dataに格納します。dataは日次データを表すpandas.Seriesオブジェクトです。Plain textCopy to clipboardOpen code in new windowEnlighterJS 3 Syntax Highlighterdata = pd.Series([10, 12, 14, 13, 15, 16,18, 20, 19, 21, 22, 23])data = pd.Series( [10, 12, 14, 13, 15, 16, 18, 20, 19, 21, 22, 23])data = pd.Series( [10, 12, 14, 13, 15, 16, 18, 20, 19, 21, 22, 23])インデックスの取得します。
indexはdataのインデックスを表すnumpy配列です。Plain textCopy to clipboardOpen code in new windowEnlighterJS 3 Syntax Highlighterindex = np.arange(len(data))index = np.arange(len(data))index = np.arange(len(data))
トレンドの推定します。
Plain textCopy to clipboardOpen code in new windowEnlighterJS 3 Syntax HighlighterX = sm.add_constant(index)model = sm.OLS(data, X).fit()trend = model.predict(X)X = sm.add_constant(index) model = sm.OLS(data, X).fit() trend = model.predict(X)X = sm.add_constant(index) model = sm.OLS(data, X).fit() trend = model.predict(X)
Xはインデックスに定数項を追加したものです。これは回帰モデルの設計行列(定数項の列がすべて1で、残りは説明変数の値、今回の説明変数はインデックスつまり0,1,2,……の連番)です。modelに、最小二乗法回帰で学習(sm.OLS(data, X).fit())させた結果であるモデルです。trendは回帰モデルを使用して予測されたトレンド値です。
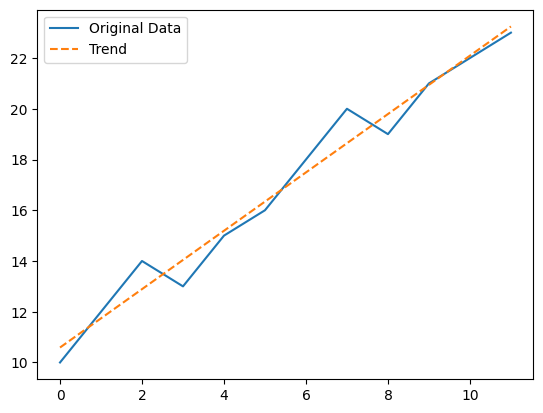
元の時系列データ(Original Data)と抽出したトレンド(Trend)を表示します。
Plain textCopy to clipboardOpen code in new windowEnlighterJS 3 Syntax Highlighterplt.plot(data, label='Original Data')plt.plot(trend, label='Trend', linestyle='--')plt.legend()plt.show()plt.plot(data, label='Original Data') plt.plot(trend, label='Trend', linestyle='--') plt.legend() plt.show()plt.plot(data, label='Original Data') plt.plot(trend, label='Trend', linestyle='--') plt.legend() plt.show()

- 時系列データのトレンド推定手法
-
時系列データのトレンド推定手法にはいくつかの方法があります。
以下に代表的な手法を説明します。
移動平均法 (Moving Average)
- 移動平均法は、データの変動を平滑化するために使用されます。
- 一定の期間のデータの平均を計算し、その平均値をトレンドとして使用します。
- 短期的な変動を除去し、長期的なトレンドを明らかにするのに適しています。
最小二乗法回帰 (Ordinary Least Squares Regression)
- 最小二乗法回帰は、データに対して直線や多項式などの関数をフィットさせる方法です。
- データポイントと回帰直線(または曲線)との距離の二乗和を最小化することで、トレンドを推定します。
- 線形のトレンドを推定するとき、連番0,1,2,……の説明変数を使います。
- 線形回帰や多項式回帰が一般的です。
Hodrick-Prescottフィルター (Hodrick-Prescott Filter)
- Hodrick-Prescottフィルターは、経済学でよく使用される手法で、時系列データをトレンド成分とサイクル成分に分解します。
- スムージングパラメータを調整することで、トレンドの滑らかさを制御できます。
指数平滑法 (Exponential Smoothing)
- 指数平滑法は、過去のデータに指数的に減少する重みを付けて平滑化する方法です。
- 単純指数平滑法、二重指数平滑法、三重指数平滑法などがあります。
- 特に、季節性やトレンドを持つデータに対して有効です。
Fourier変換 (Fourier Transform)
- Fourier変換は、時系列データを周波数成分に分解する手法です。
- データの周期的なパターンを分析するのに適しており、トレンド成分を抽出するために逆Fourier変換を使用することもあります。
ローカル回帰 (LOESS/LOWESS)
- ローカル回帰は、データの局所的な部分に対して回帰を行う手法です。
- データの一部に対して低次の多項式をフィットさせ、その結果を結合して全体のトレンドを推定します。
- 非線形なトレンドを捉えるのに適しています。
これらの手法は、それぞれのデータの特性や目的に応じて使い分けることが重要です。
例えば、短期的な変動を除去して長期的なトレンドを把握したい場合は移動平均法や最小二乗法回帰が適していますし、周期的なパターンを分析したい場合はFourier変換が有効です。
- 実行例
-
時系列データのトレンド推定手法の実行例を示します。
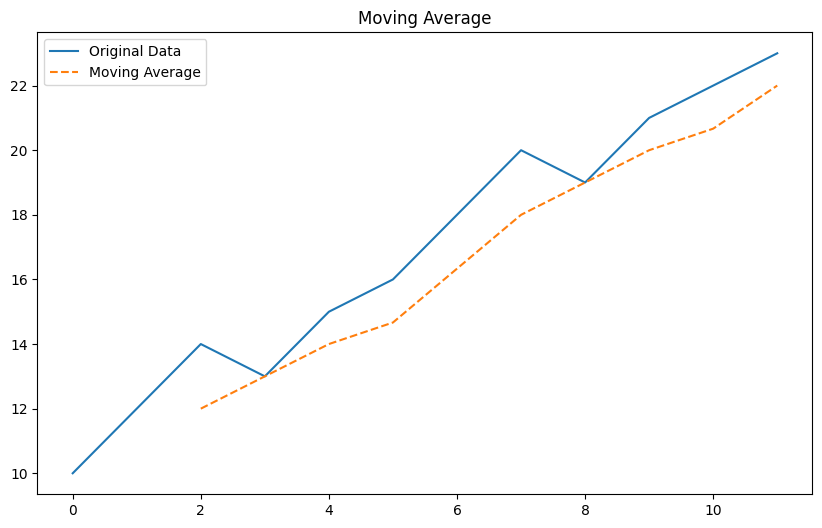
移動平均法 (Moving Average)
以下、コードです。
Plain textCopy to clipboardOpen code in new windowEnlighterJS 3 Syntax Highlighter# 移動平均法 (Moving Average)import matplotlib.pyplot as pltdata = pd.Series([10, 12, 14, 13, 15, 16, 18, 20, 19, 21, 22, 23])window_size = 3moving_average = data.rolling(window=window_size).mean()plt.figure(figsize=(10, 6))plt.plot(data, label='Original Data')plt.plot(moving_average, label='Moving Average', linestyle='--')plt.legend()plt.title('Moving Average')plt.show()# 移動平均法 (Moving Average) import matplotlib.pyplot as plt data = pd.Series([10, 12, 14, 13, 15, 16, 18, 20, 19, 21, 22, 23]) window_size = 3 moving_average = data.rolling(window=window_size).mean() plt.figure(figsize=(10, 6)) plt.plot(data, label='Original Data') plt.plot(moving_average, label='Moving Average', linestyle='--') plt.legend() plt.title('Moving Average') plt.show()# 移動平均法 (Moving Average) import matplotlib.pyplot as plt data = pd.Series([10, 12, 14, 13, 15, 16, 18, 20, 19, 21, 22, 23]) window_size = 3 moving_average = data.rolling(window=window_size).mean() plt.figure(figsize=(10, 6)) plt.plot(data, label='Original Data') plt.plot(moving_average, label='Moving Average', linestyle='--') plt.legend() plt.title('Moving Average') plt.show()以下、実行結果です。
最小二乗法回帰 (Ordinary Least Squares Regression)
以下、コードです。
Plain textCopy to clipboardOpen code in new windowEnlighterJS 3 Syntax Highlighter# 最小二乗法回帰 (Ordinary Least Squares Regression)X = sm.add_constant(index)model = sm.OLS(data, X).fit()trend = model.predict(X)plt.figure(figsize=(10, 6))plt.plot(data, label='Original Data')plt.plot(trend, label='OLS Regression Trend', linestyle='--')plt.legend()plt.title('OLS Regression')plt.show()# 最小二乗法回帰 (Ordinary Least Squares Regression) X = sm.add_constant(index) model = sm.OLS(data, X).fit() trend = model.predict(X) plt.figure(figsize=(10, 6)) plt.plot(data, label='Original Data') plt.plot(trend, label='OLS Regression Trend', linestyle='--') plt.legend() plt.title('OLS Regression') plt.show()# 最小二乗法回帰 (Ordinary Least Squares Regression) X = sm.add_constant(index) model = sm.OLS(data, X).fit() trend = model.predict(X) plt.figure(figsize=(10, 6)) plt.plot(data, label='Original Data') plt.plot(trend, label='OLS Regression Trend', linestyle='--') plt.legend() plt.title('OLS Regression') plt.show()以下、実行結果です。
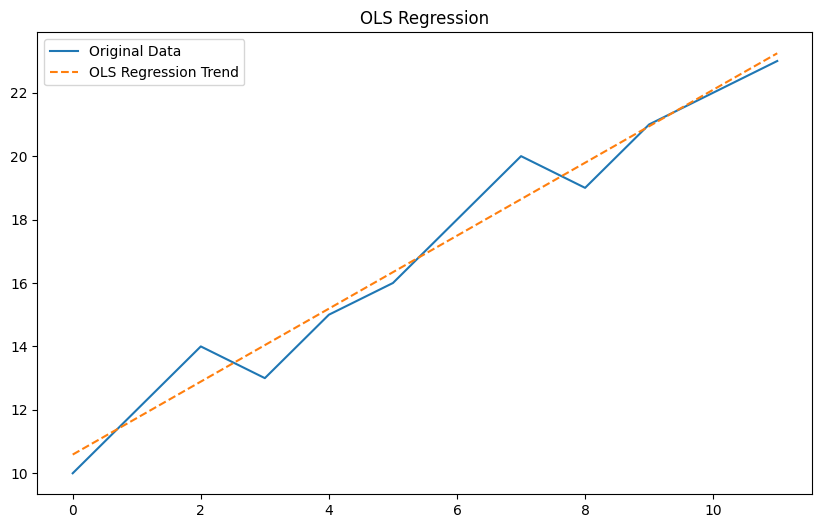
Hodrick-Prescottフィルター (Hodrick-Prescott Filter)
以下、コードです。
Plain textCopy to clipboardOpen code in new windowEnlighterJS 3 Syntax Highlighter# Hodrick-Prescottフィルター (Hodrick-Prescott Filter)cycle, trend_hp = sm.tsa.filters.hpfilter(data, lamb=1600)plt.figure(figsize=(10, 6))plt.plot(data, label='Original Data')plt.plot(trend_hp, label='HP Filter Trend', linestyle='--')plt.legend()plt.title('Hodrick-Prescott Filter')plt.show()# Hodrick-Prescottフィルター (Hodrick-Prescott Filter) cycle, trend_hp = sm.tsa.filters.hpfilter(data, lamb=1600) plt.figure(figsize=(10, 6)) plt.plot(data, label='Original Data') plt.plot(trend_hp, label='HP Filter Trend', linestyle='--') plt.legend() plt.title('Hodrick-Prescott Filter') plt.show()# Hodrick-Prescottフィルター (Hodrick-Prescott Filter) cycle, trend_hp = sm.tsa.filters.hpfilter(data, lamb=1600) plt.figure(figsize=(10, 6)) plt.plot(data, label='Original Data') plt.plot(trend_hp, label='HP Filter Trend', linestyle='--') plt.legend() plt.title('Hodrick-Prescott Filter') plt.show()以下、実行結果です。
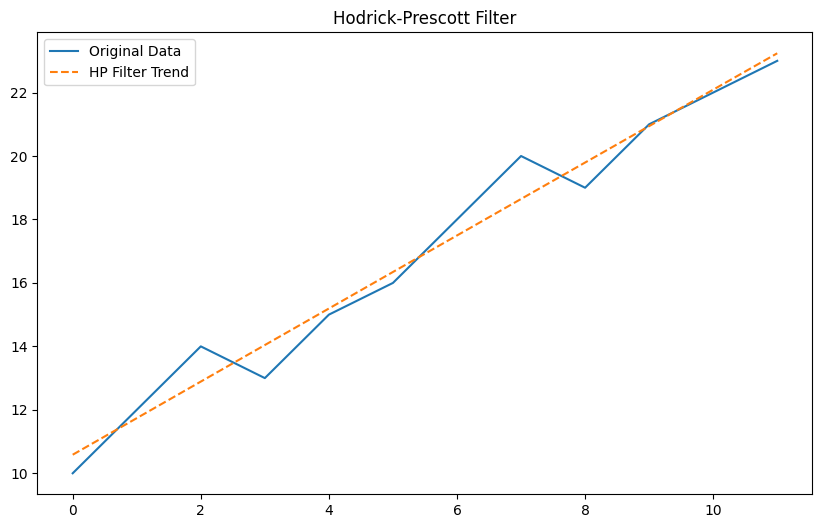
指数平滑法 (Exponential Smoothing)
以下、コードです。
Plain textCopy to clipboardOpen code in new windowEnlighterJS 3 Syntax Highlighter# 指数平滑法 (Exponential Smoothing)from statsmodels.tsa.holtwinters import ExponentialSmoothingmodel_es = ExponentialSmoothing(data, trend='add').fit()trend_es = model_es.fittedvaluesplt.figure(figsize=(10, 6))plt.plot(data, label='Original Data')plt.plot(trend_es, label='Exponential Smoothing Trend', linestyle='--')plt.legend()plt.title('Exponential Smoothing')plt.show()# 指数平滑法 (Exponential Smoothing) from statsmodels.tsa.holtwinters import ExponentialSmoothing model_es = ExponentialSmoothing(data, trend='add').fit() trend_es = model_es.fittedvalues plt.figure(figsize=(10, 6)) plt.plot(data, label='Original Data') plt.plot(trend_es, label='Exponential Smoothing Trend', linestyle='--') plt.legend() plt.title('Exponential Smoothing') plt.show()# 指数平滑法 (Exponential Smoothing) from statsmodels.tsa.holtwinters import ExponentialSmoothing model_es = ExponentialSmoothing(data, trend='add').fit() trend_es = model_es.fittedvalues plt.figure(figsize=(10, 6)) plt.plot(data, label='Original Data') plt.plot(trend_es, label='Exponential Smoothing Trend', linestyle='--') plt.legend() plt.title('Exponential Smoothing') plt.show()以下、実行結果です。
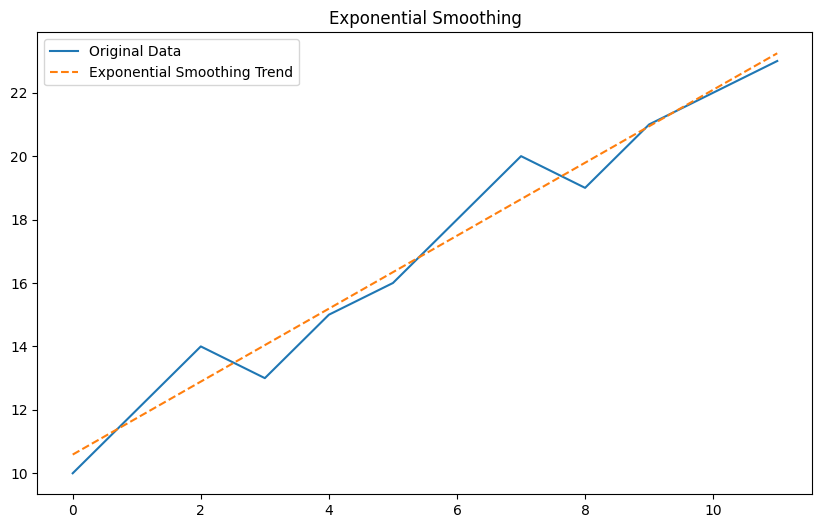
Fourier変換 (Fourier Transform)
以下、コードです。
Plain textCopy to clipboardOpen code in new windowEnlighterJS 3 Syntax Highlighter# Fourier変換 (Fourier Transform)from scipy.fft import fft, ifft# Fourier変換data_fft = fft(data)# 高周波成分を除去n = len(data)cutoff = 2 # 低周波成分の数data_fft[cutoff:-cutoff] = 0# 逆Fourier変換trend_fft = ifft(data_fft).realplt.figure(figsize=(10, 6))plt.plot(data, label='Original Data')plt.plot(trend_fft, label='Fourier Transform Trend', linestyle='--')plt.legend()plt.title('Fourier Transform')plt.show()# Fourier変換 (Fourier Transform) from scipy.fft import fft, ifft # Fourier変換 data_fft = fft(data) # 高周波成分を除去 n = len(data) cutoff = 2 # 低周波成分の数 data_fft[cutoff:-cutoff] = 0 # 逆Fourier変換 trend_fft = ifft(data_fft).real plt.figure(figsize=(10, 6)) plt.plot(data, label='Original Data') plt.plot(trend_fft, label='Fourier Transform Trend', linestyle='--') plt.legend() plt.title('Fourier Transform') plt.show()# Fourier変換 (Fourier Transform) from scipy.fft import fft, ifft # Fourier変換 data_fft = fft(data) # 高周波成分を除去 n = len(data) cutoff = 2 # 低周波成分の数 data_fft[cutoff:-cutoff] = 0 # 逆Fourier変換 trend_fft = ifft(data_fft).real plt.figure(figsize=(10, 6)) plt.plot(data, label='Original Data') plt.plot(trend_fft, label='Fourier Transform Trend', linestyle='--') plt.legend() plt.title('Fourier Transform') plt.show()以下、実行結果です。
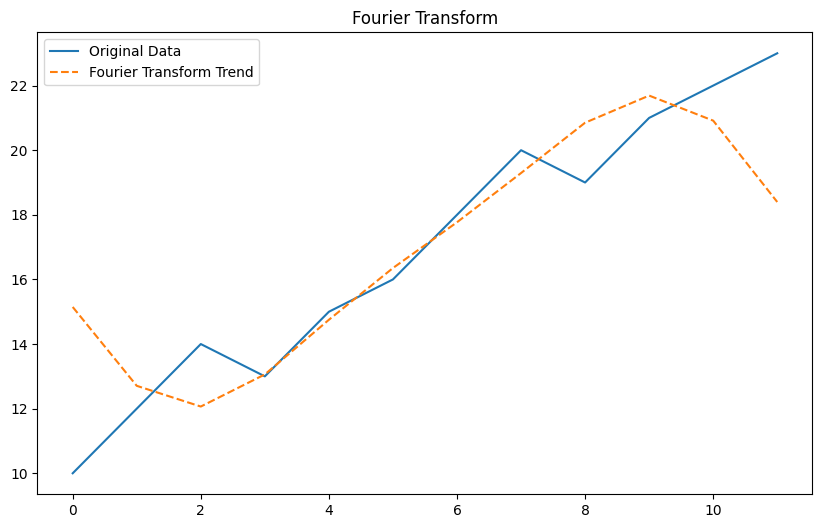
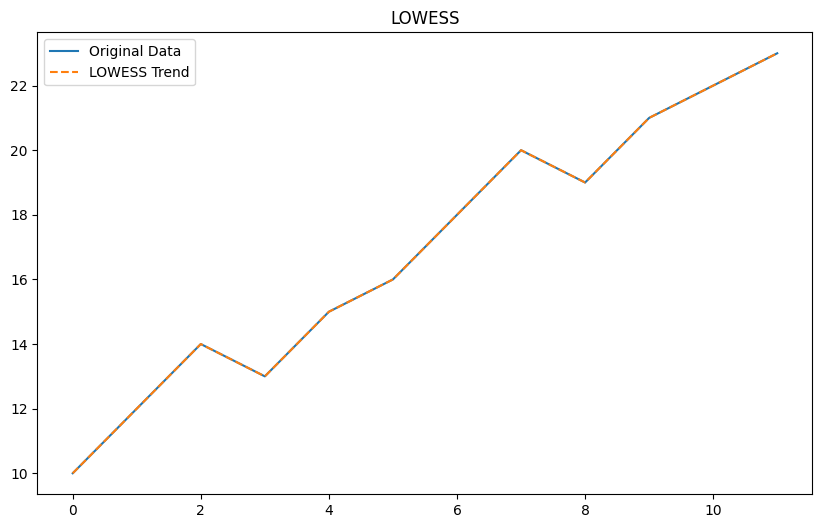
ローカル回帰 (LOESS/LOWESS)
以下、コードです。
Plain textCopy to clipboardOpen code in new windowEnlighterJS 3 Syntax Highlighter# ローカル回帰 (LOESS/LOWESS)from statsmodels.nonparametric.smoothers_lowess import lowess# LOWESSの適用trend_lowess = lowess(data, index, frac=0.3)[:, 1]plt.figure(figsize=(10, 6))plt.plot(data, label='Original Data')plt.plot(trend_lowess, label='LOWESS Trend', linestyle='--')plt.legend()plt.title('LOWESS')plt.show()# ローカル回帰 (LOESS/LOWESS) from statsmodels.nonparametric.smoothers_lowess import lowess # LOWESSの適用 trend_lowess = lowess(data, index, frac=0.3)[:, 1] plt.figure(figsize=(10, 6)) plt.plot(data, label='Original Data') plt.plot(trend_lowess, label='LOWESS Trend', linestyle='--') plt.legend() plt.title('LOWESS') plt.show()# ローカル回帰 (LOESS/LOWESS) from statsmodels.nonparametric.smoothers_lowess import lowess # LOWESSの適用 trend_lowess = lowess(data, index, frac=0.3)[:, 1] plt.figure(figsize=(10, 6)) plt.plot(data, label='Original Data') plt.plot(trend_lowess, label='LOWESS Trend', linestyle='--') plt.legend() plt.title('LOWESS') plt.show()以下、実行結果です。