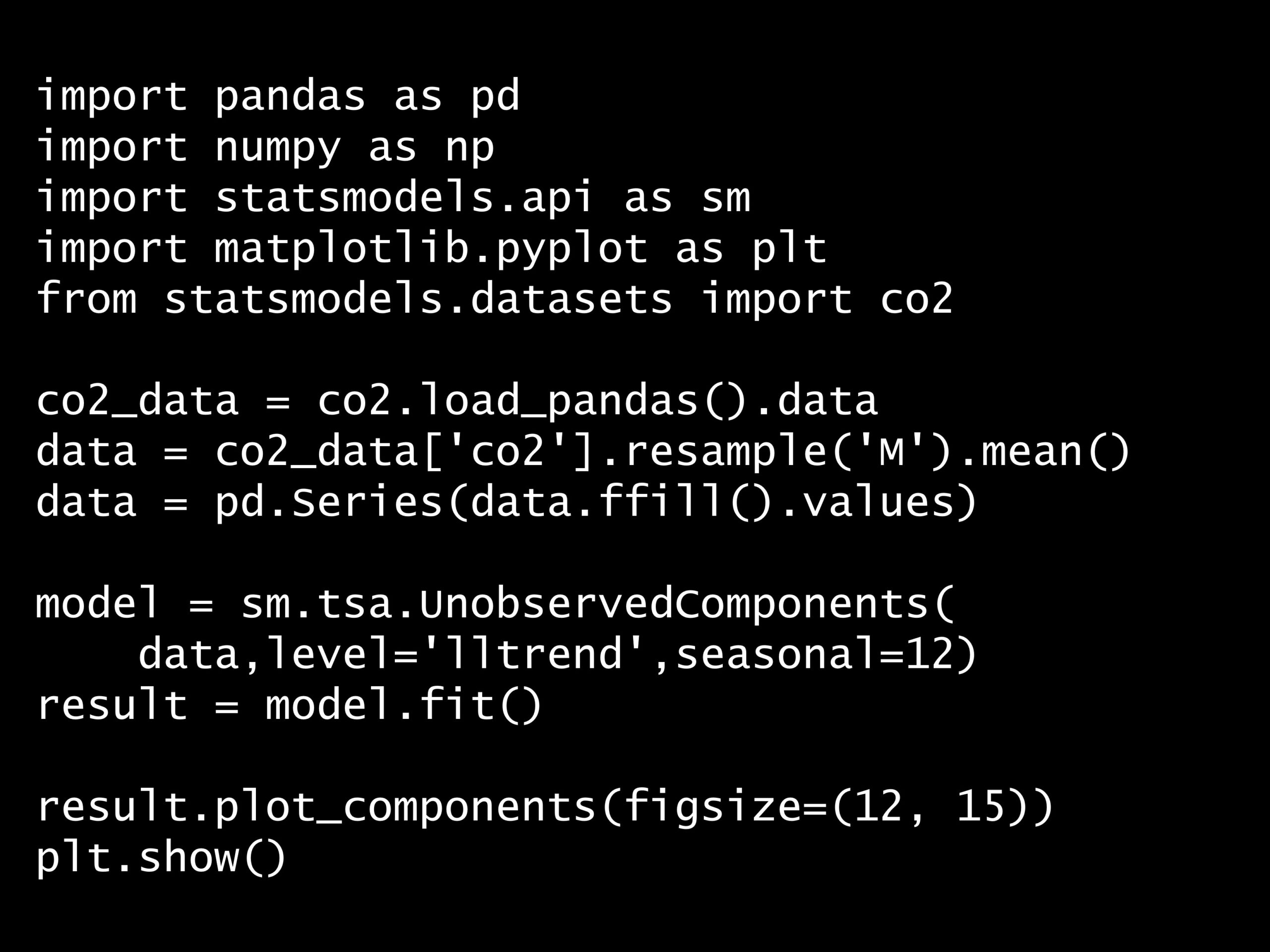
Python 時系列分析 1,000本ノック– ノック62: 状態空間モデル –

問題
答え
解説

次の Python コードは、どの種類のモデルを実装していますか？

Python コード:

import pandas as pd

import numpy as np

import statsmodels.api as sm

import matplotlib.pyplot as plt

from statsmodels.datasets import co2

co2_data = co2.load_pandas().data

data = co2_data['co2'].resample('M').mean()

data = pd.Series(data.ffill().values)

model = sm.tsa.UnobservedComponents(

data,level='lltrend',seasonal=12)

result = model.fit()

result.plot_components(figsize=(12, 15))

plt.show()

import pandas as pd import numpy as np import statsmodels.api as sm import matplotlib.pyplot as plt from statsmodels.datasets import co2 co2_data = co2.load_pandas().data data = co2_data['co2'].resample('M').mean() data = pd.Series(data.ffill().values) model = sm.tsa.UnobservedComponents( data,level='lltrend',seasonal=12) result = model.fit() result.plot_components(figsize=(12, 15)) plt.show()

import pandas as pd
import numpy as np
import statsmodels.api as sm
import matplotlib.pyplot as plt
from statsmodels.datasets import co2

co2_data = co2.load_pandas().data
data = co2_data['co2'].resample('M').mean()
data = pd.Series(data.ffill().values)

model = sm.tsa.UnobservedComponents(
    data,level='lltrend',seasonal=12)
result = model.fit()

result.plot_components(figsize=(12, 15))
plt.show()

回答の選択肢:

(A) ローカルレベルモデル
(B) ローカル線形トレンドモデル
(C) ランダムトレンドモデル
(D) 確定的トレンドモデル

コードの解説

このコードは、CO2濃度の時系列データに対して、UCモデルと呼ばれる状態空間モデルを使用してトレンドと季節性を分離する方法を示しています。

import pandas as pd

import numpy as np

import statsmodels.api as sm

import matplotlib.pyplot as plt

from statsmodels.datasets import co2

co2_data = co2.load_pandas().data

data = co2_data['co2'].resample('M').mean()

data = pd.Series(data.ffill().values)

model = sm.tsa.UnobservedComponents(

data,level='lltrend',seasonal=12)

result = model.fit()

result.plot_components(figsize=(12, 15))

plt.show()

import pandas as pd
import numpy as np
import statsmodels.api as sm
import matplotlib.pyplot as plt
from statsmodels.datasets import co2

co2_data = co2.load_pandas().data
data = co2_data['co2'].resample('M').mean()
data = pd.Series(data.ffill().values)

model = sm.tsa.UnobservedComponents(
    data,level='lltrend',seasonal=12)
result = model.fit()

result.plot_components(figsize=(12, 15))
plt.show()

詳しく説明します。

先ず、CO2データの読み込みと前処理をします。

co2.load_pandas().dataを使用してCO2データを読み込みます。

data = co2_data['co2'].resample('M').mean()でデータを月次にリサンプリングし、月ごとの平均値を計算します。

data = pd.Series(data.ffill().values)で欠損値を前方補完（ffill）し、pandas.Seriesオブジェクトに変換します。

dataには、以下のようなデータが格納されています。

0      316.100000
1      317.200000
2      317.433333
3      317.433333
4      315.625000
          ...    
521    369.425000
522    367.880000
523    368.050000
524    369.375000
525    371.020000
Length: 526, dtype: float64

次に、状態空間モデルの定義と学習をします。

sm.tsa.UnobservedComponentsを使用して状態空間モデルを定義します。ここでは、ローカル線形トレンド（level='lltrend'）と季節性（seasonal=12）を含むモデルを指定しています。

result = model.fit()でモデルをデータに適合させます。

最後に、モデルのコンポーネントをプロットします。

result.plot_components(figsize=(12, 15))でモデルのコンポーネント（トレンド、季節性、残差など）をプロットします。

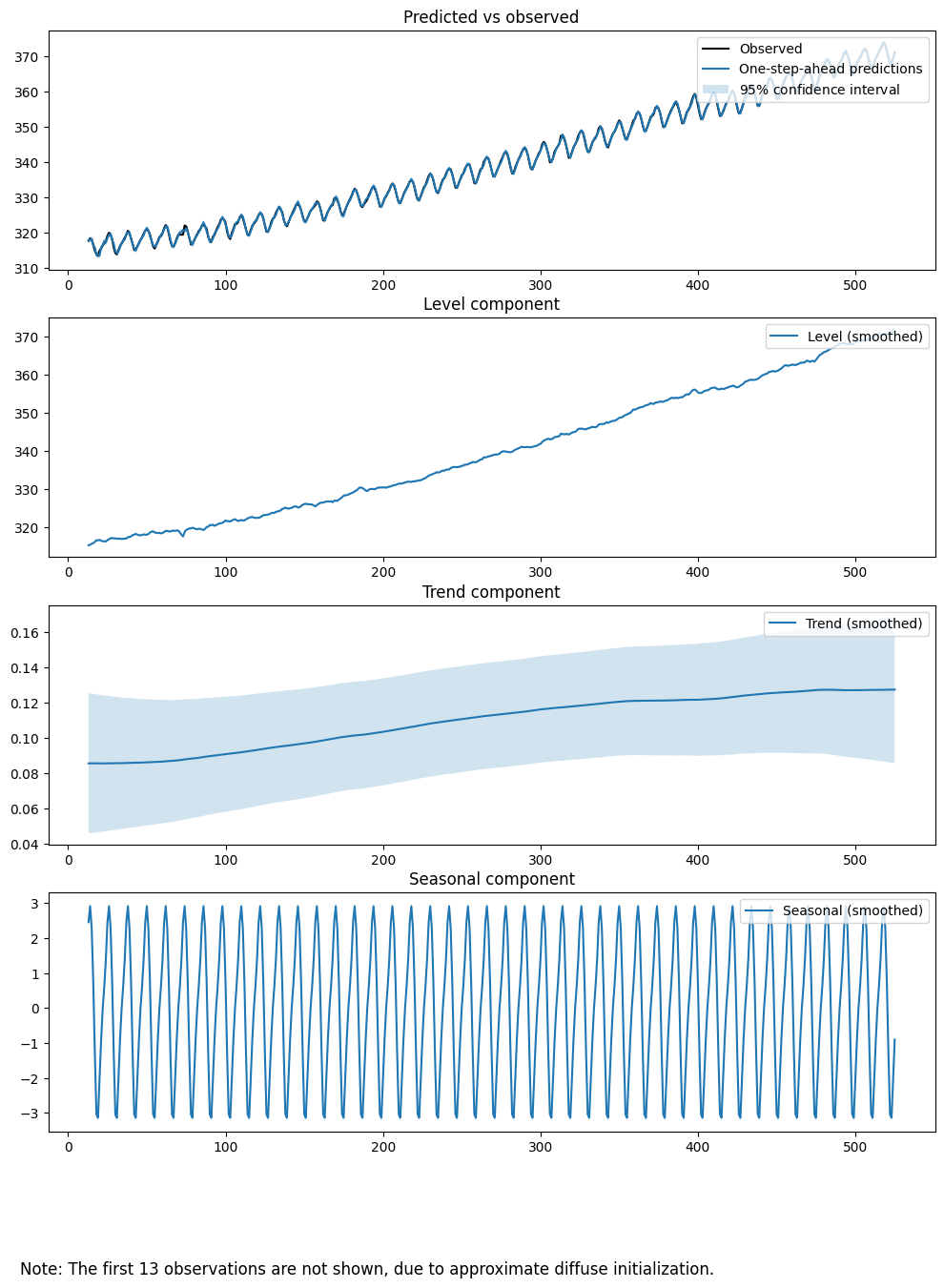
プロットの各成分の説明を簡単にします。

Predicted vs Observed (予測値 vs 観測値)

Observed（観測値）: 黒い線で表示されているのが実際の観測データです。
One-step-ahead predictions（1ステップ先の予測値）: 青い線で表示されており、観測データに基づく予測値です。
95% confidence interval（95%信頼区間）: 薄青い範囲で表示されており、予測値の信頼区間を示します。

Level Component (レベル成分)

このプロットは時系列データの基礎的な水準の変動を示しています。
青い線はスムージングされたレベル成分を表しています。

Trend Component (トレンド成分)

時系列データの長期的な傾向を示しています。
青い線がスムージングされたトレンド成分で、薄青い範囲がその信頼区間を示します。

Seasonal Component (季節成分)

データ内の繰り返し発生する季節パターンを示しています。
青い線はスムージングされた季節成分を表しています。

状態空間モデルとは？

状態空間モデルは、観測データとその背後にある潜在的な状態（状態変数）をモデル化するためのフレームワークです。

状態空間モデルは、以下の2つの方程式で構成されます。

状態方程式 (State Equation)
状態変数の時間的な進化を記述します。

\displaystyle x_t = F x_{t-1} + G u_t + w_t

ここで、 $x_t$ は時刻 $t$ の状態変数、 $F$ は状態遷移行列、 $G$ は制御行列、 $u_t$ は制御入力、 $w_t$ はプロセスノイズです。

観測方程式 (Observation Equation)
観測データと状態変数の関係を記述します。

\displaystyle y_t = H x_t + v_t

ここで、 $y_t$ は時刻 $t$ の観測データ、 $H$ は観測行列、 $v_t$ は観測ノイズです。

状態空間モデルは、カルマンフィルターや粒子フィルターなどのアルゴリズムを使用して、状態変数の推定や予測を行います。

UCモデルとは？

UCモデル（Univariate Unobserved Components Time Series Model）は、時系列データをいくつかの基本的な構成要素に分解するモデルで、状態空間モデルの一種です。

このモデルは、各成分が観測データにどのように寄与しているかを明確にし、データのパターンを理解するために使用されます。

UCモデルは、一変量時系列データを以下の主要な構成要素に分解します。

レベル (Level): データの基礎的な水準
トレンド (Trend): データの長期的な動向
季節性 (Seasonal): 一定の周期で繰り返されるパターン
サイクル (Cycle): 季節性とは異なる周期的なパターン
不規則成分 (Irregular): 残差やノイズ

UCモデルは、観測された時系列データ $y_t$ を以下のように表現します。

\displaystyle y_t=μ_t+\beta_t+γ_t+c_t+ϵ_t

$μ_t$ ：レベル (Level)
$\beta_t$ ：トレンド (Trend)
$γ_t$ ：季節性 (Seasonal)
$c_t$ ：サイクル (Cycle)
$ϵ_t$ ：不規則成分 (Irregular)

状態空間モデルの状態方程式および観測方程式の形で表現すると、以下のようになります。

観測方程式

\displaystyle y_t=μ_t+\beta_t+γ_t+c_t+ϵ_t

状態方程式

レベル (Level)： $\displaystyle μ_{t+1}=μ_t+η_t$
トレンド (Trend)： $\displaystyle \beta_{t+1}=\beta_t+ζ_t$
季節性 (Seasonal)： $\displaystyle γ_{t+1}=−\sum_{i=1}^{s−1}γ_{t−i}+ω_t$

η_t, ζ_t, ω_t

はノイズ項、

s

は周期です。

statsmodelsライブラリを用いたUCモデルの実装

Pythonのstatsmodelsライブラリに含まれるクラスに、UCモデル（状態空間モデル）を実装するUnobservedComponentsクラスがあります。

このUCモデルは、時系列データをいくつかの基本的な構成要素（レベル、トレンド、季節性、サイクル、不規則成分）に分解し、それぞれの成分がデータにどのように寄与しているかを理解するために使用されます。

以下は、主な引数です。

endog: モデルに適合させる時系列データ。これは主要な入力データです。
level: レベル成分を含むかどうかを指定します。TrueまたはFalse、モデル名を指定します。
trend: トレンド成分を含むかどうかを指定します。TrueまたはFalseを指定します。
seasonal: 季節性成分を指定します。例えば、季節性の周期を整数で指定します。
freq_seasonal: 周波数ベースの季節性成分を指定します。リストで複数の季節性成分を指定することも可能です。
cycle: サイクル成分を含むかどうかを指定します。TrueまたはFalseを指定します。
autoregressive: 自己回帰成分の次数を指定します。
irregular: 不規則成分を含むかどうかを指定します。TrueまたはFalseを指定します。

以下、コード例です。

import statsmodels.api as sm

# 例の時系列データを読み込む

data = sm.datasets.macrodata.load_pandas().data['realgdp']

# Unobserved Componentsモデルを定義

mod = sm.tsa.UnobservedComponents(data, level='llevel', seasonal=12)

# モデルを適合

res = mod.fit()

# 結果を表示

print(res.summary())

# 成分をプロット

res.plot_components(figsize=(15, 10))

import statsmodels.api as sm # 例の時系列データを読み込む data = sm.datasets.macrodata.load_pandas().data['realgdp'] # Unobserved Componentsモデルを定義 mod = sm.tsa.UnobservedComponents(data, level='llevel', seasonal=12) # モデルを適合 res = mod.fit() # 結果を表示 print(res.summary()) # 成分をプロット res.plot_components(figsize=(15, 10))

import statsmodels.api as sm

# 例の時系列データを読み込む
data = sm.datasets.macrodata.load_pandas().data['realgdp']

# Unobserved Componentsモデルを定義
mod = sm.tsa.UnobservedComponents(data, level='llevel', seasonal=12)

# モデルを適合
res = mod.fit()

# 結果を表示
print(res.summary())

# 成分をプロット
res.plot_components(figsize=(15, 10))

以下、実行例です。

                            Unobserved Components Results                            
=====================================================================================
Dep. Variable:                       realgdp   No. Observations:                  203
Model:                           local level   Log Likelihood               -1124.849
                   + stochastic seasonal(12)   AIC                           2255.699
Date:                       Mon, 15 Jul 2024   BIC                           2265.456
Time:                               05:48:05   HQIC                          2259.651
Sample:                                    0                                         
                                       - 203                                         
Covariance Type:                         opg                                         
====================================================================================
                       coef    std err          z      P>|z|      [0.025      0.975]
------------------------------------------------------------------------------------
sigma2.irregular  2.679e-05    514.651   5.21e-08      1.000   -1008.696    1008.697
sigma2.level      6425.4591    895.957      7.172      0.000    4669.415    8181.503
sigma2.seasonal    6.41e-07     12.693   5.05e-08      1.000     -24.877      24.877
===================================================================================
Ljung-Box (L1) (Q):                  31.53   Jarque-Bera (JB):                61.79
Prob(Q):                              0.00   Prob(JB):                         0.00
Heteroskedasticity (H):               3.27   Skew:                            -0.67
Prob(H) (two-sided):                  0.00   Kurtosis:                         5.45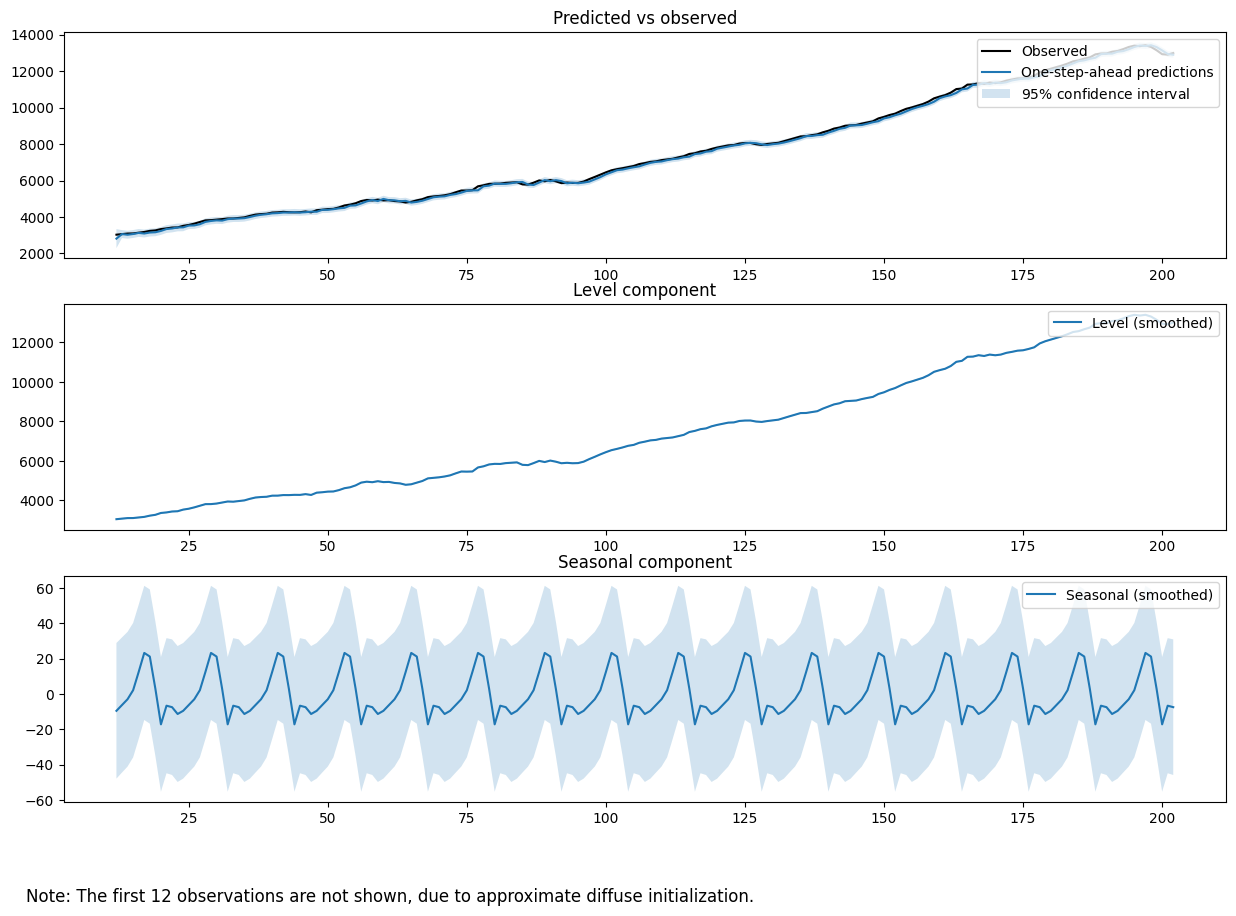
===================================================================================

この例で使用されているモデルの構成要素は以下の通りです。

level='local level'：ローカルレベルモデルを指定しています。ローカルレベルモデルは、時系列データのレベルが時間とともにランダムウォークのように変化するモデルです。
seasonal=12：季節性成分を指定しています。この例では、12期間（例えば、12か月）の季節性があることを示しています。

trendに、具体的なモデルをしてすることができます。以下、一覧表です。

モデル名	フル文字列構文	略語構文	モデル
トレンドなし	irregular	ntrend	$y_t = \epsilon_t$
固定切片	fixed intercept	ntrend	$y_t = \mu$
確定的定数	deterministic constant	dconstant	$y_t = \mu + \epsilon_t$
ローカルレベル	local level	llevel	$y_t = \mu_t + \epsilon_t \\ \mu_t = \mu_{t-1} + \eta_t$
ランダムウォーク	random walk	rwalk	$y_t = \mu_t \\ \mu_t = \mu_{t-1} + \eta_t$
固定傾斜	fixed slope	rtrend	$y_t = \mu_t \\ \mu_t = \mu_{t-1} + \beta$
確定的トレンド	deterministic trend	dtrend	$y_t = \mu_t + \epsilon_t \\ \mu_t = \mu_{t-1} + \beta$
ローカル線形確定的トレンド	local linear deterministic trend	lldtrend	$y_t = \mu_t + \epsilon_t \\ \mu_t = \mu_{t-1} + \beta_{t-1} + \eta_t \\ \beta_t = \beta_{t-1} + \eta_t$
ドリフト付きランダムウォーク	random walk with drift	rwdrift	$y_t = \mu_t \\ \mu_t = \mu_{t-1} + \beta + \eta_t$
ローカル線形トレンド	local linear trend	lltrend	$y_t = \mu_t + \epsilon_t \\ \mu_t = \mu_{t-1} + \beta_{t-1} + \eta_t \\ \beta_t = \beta_{t-1} + \zeta_t$
スムーストレンド	smooth trend	strend	$y_t = \mu_t + \epsilon_t \\ \mu_t = \mu_{t-1} + \beta_{t-1} \\ \beta_t = \beta_{t-1} + \zeta_t$
ランダムトレンド	random trend	rtrend	$y_t = \mu_t + \epsilon_t \\ \mu_t = \mu_{t-1} + \beta_{t-1} + \eta_t \\ \beta_t = \beta_{t-1} + \zeta_t$

各UCモデルの簡易説明