- 問題
- 答え
- 解説
Python コード:
import numpy as np import pandas as pd import statsmodels.tsa.statespace.structural as ts np.random.seed(42) data = pd.Series(np.random.randn(50).cumsum() + 10) ml = ts.UnobservedComponents(data,level='llevel') results = ml.fit() filtered_state = results.filtered_state print(filtered_state)
回答の選択肢:
(A) データの未来の値の予測
(B) データの隠れた状態の過去の推定値
(C) データの観測値そのもの
(D) データのノイズ成分
RUNNING THE L-BFGS-B CODE
* * *
Machine precision = 2.220D-16
N = 2 M = 10
At X0 0 variables are exactly at the bounds
At iterate 0 f= 2.44963D+00 |proj g|= 1.84319D-01
At iterate 5 f= 1.34896D+00 |proj g|= 2.61940D-03
* * *
Tit = total number of iterations
Tnf = total number of function evaluations
Tnint = total number of segments explored during Cauchy searches
Skip = number of BFGS updates skipped
Nact = number of active bounds at final generalized Cauchy point
Projg = norm of the final projected gradient
F = final function value
* * *
N Tit Tnf Tnint Skip Nact Projg F
2 8 17 1 0 0 1.390D-06 1.349D+00
F = 1.3489449217544023
CONVERGENCE: NORM_OF_PROJECTED_GRADIENT_<=_PGTOL
[[10.49671415 10.35844985 11.00613839 12.52916825 12.29501487 12.06087791
13.64009073 14.40752546 13.93805107 14.48061112 14.01719342 13.55146367
13.79342594 11.8801457 10.15522787 9.59294034 8.58010922 8.89435655
7.98633247 6.57402877 8.03967754 7.81390124 7.88142944 6.45668126
5.91229853 6.02322112 4.87222755 5.24792556 4.64728687 4.35559312
3.75388651 5.6061647 5.59266747 4.53495654 5.35750146 4.13665781
4.3455214 2.38585128 1.05766523 1.25452646 1.99299304 2.16436132
2.04871304 1.74760935 0.26908736 -0.45075685 -0.91139562 0.1457266
0.48934489 -1.27369526]]
This problem is unconstrained.
正解: (B)
回答の選択肢:
(A) データの未来の値の予測
(B) データの隠れた状態の過去の推定値
(C) データの観測値そのもの
(D) データのノイズ成分
- コードの解説
-
このコードは、状態空間モデルを使用して時系列データの隠れた状態を推定しています。具体的には、
statsmodelsライブラリのUnobservedComponentsモデルを用いて、データのローカルレベルを推定しています。Plain textCopy to clipboardOpen code in new windowEnlighterJS 3 Syntax Highlighterimport numpy as npimport pandas as pdimport statsmodels.tsa.statespace.structural as tsnp.random.seed(42)data = pd.Series(np.random.randn(50).cumsum() + 10)ml = ts.UnobservedComponents(data,level='llevel')results = ml.fit()filtered_state = results.filtered_stateprint(filtered_state)import numpy as np import pandas as pd import statsmodels.tsa.statespace.structural as ts np.random.seed(42) data = pd.Series(np.random.randn(50).cumsum() + 10) ml = ts.UnobservedComponents(data,level='llevel') results = ml.fit() filtered_state = results.filtered_state print(filtered_state)import numpy as np import pandas as pd import statsmodels.tsa.statespace.structural as ts np.random.seed(42) data = pd.Series(np.random.randn(50).cumsum() + 10) ml = ts.UnobservedComponents(data,level='llevel') results = ml.fit() filtered_state = results.filtered_state print(filtered_state)
詳しく説明します。
dataという名前のpandas.Seriesを作成し、累積和に10を加えたデータを生成します。Plain textCopy to clipboardOpen code in new windowEnlighterJS 3 Syntax Highlighternp.random.seed(42)data = pd.Series(np.random.randn(50).cumsum() + 10)np.random.seed(42) data = pd.Series(np.random.randn(50).cumsum() + 10)np.random.seed(42) data = pd.Series(np.random.randn(50).cumsum() + 10)
dataには、以下のようなデータが格納されています。0 10.496714 1 10.358450 2 11.006138 3 12.529168 4 12.295015 ... 46 -0.911396 47 0.145727 48 0.489345 49 -1.273695 dtype: float64UnobservedComponentsを使用して、を使用して、データに対して「ローカルレベル」モデルを定義します。ml.fit()を呼び出してモデルをデータにフィットさせ、結果をresultsに格納します。Plain textCopy to clipboardOpen code in new windowEnlighterJS 3 Syntax Highlighterml = ts.UnobservedComponents(data,level='llevel')results = ml.fit()ml = ts.UnobservedComponents(data,level='llevel') results = ml.fit()ml = ts.UnobservedComponents(data,level='llevel') results = ml.fit()
results.filtered_stateを使用して、フィルタリングされた状態を取得し、filtered_stateに格納し表示します。Plain textCopy to clipboardOpen code in new windowEnlighterJS 3 Syntax Highlighterfiltered_state = results.filtered_stateprint(filtered_state)filtered_state = results.filtered_state print(filtered_state)filtered_state = results.filtered_state print(filtered_state)
RUNNING THE L-BFGS-B CODE * * * Machine precision = 2.220D-16 N = 2 M = 10 At X0 0 variables are exactly at the bounds At iterate 0 f= 2.44963D+00 |proj g|= 1.84319D-01 At iterate 5 f= 1.34896D+00 |proj g|= 2.61940D-03 * * * Tit = total number of iterations Tnf = total number of function evaluations Tnint = total number of segments explored during Cauchy searches Skip = number of BFGS updates skipped Nact = number of active bounds at final generalized Cauchy point Projg = norm of the final projected gradient F = final function value * * * N Tit Tnf Tnint Skip Nact Projg F 2 8 17 1 0 0 1.390D-06 1.349D+00 F = 1.3489449217544023 CONVERGENCE: NORM_OF_PROJECTED_GRADIENT_<=_PGTOL [[10.49671415 10.35844985 11.00613839 12.52916825 12.29501487 12.06087791 13.64009073 14.40752546 13.93805107 14.48061112 14.01719342 13.55146367 13.79342594 11.8801457 10.15522787 9.59294034 8.58010922 8.89435655 7.98633247 6.57402877 8.03967754 7.81390124 7.88142944 6.45668126 5.91229853 6.02322112 4.87222755 5.24792556 4.64728687 4.35559312 3.75388651 5.6061647 5.59266747 4.53495654 5.35750146 4.13665781 4.3455214 2.38585128 1.05766523 1.25452646 1.99299304 2.16436132 2.04871304 1.74760935 0.26908736 -0.45075685 -0.91139562 0.1457266 0.48934489 -1.27369526]] This problem is unconstrained. - 状態空間モデルとカルマンフィルタ
-
状態空間モデルとカルマンフィルタは、時系列データの解析や予測に用いられる強力なツールです。
- リアルタイム推定: カルマンフィルタはリアルタイムで状態を推定できるため、動的なシステムの追跡に適しています。
- ノイズの除去: 観測データのノイズを効果的に除去し、真の状態を推定します。
- 適用範囲: レーダー追跡、経済予測、ロボット工学など、さまざまな分野で利用されています。
Contents [hide]
状態空間モデル
状態空間モデルは、観測データと隠れた状態(真の状態)を表現するための統計モデルです。
以下の2つの方程式で構成されます。
状態方程式
隠れた状態の時間的な変化を記述します。
観測方程式
観測データと隠れた状態の関係を記述します。
カルマンフィルタ
カルマンフィルタは、状態空間モデルに基づいて、時系列データの隠れた状態を推定するためのアルゴリズムです。
以下のステップで構成されます。
予測ステップ
次の時刻の状態とその不確実性を予測します。- 状態予測:
- 共分散予測:
更新ステップ
新しい観測データを用いて予測を更新します。- カルマンゲインの計算:
- 状態更新:
- 共分散更新:
基本的な状態空間モデル
ここでは、代表的な基本的状態空間モデルを紹介します。
ローカルレベルモデル(Local Level Model)
ローカルレベルモデル(別名:ランダムウォークプラスノイズモデル)は、最も単純な状態空間モデルの一つです。
状態方程式:
観測方程式:
ここで、
このモデルは、時間とともにランダムに変動するレベル(平均)を持つ時系列データに適しています。例えば、株価や為替レートなどの金融データ、あるいは気温データなどの環境データの分析に使用されることがあります。
ローカル線形トレンドモデル(Local Linear Trend Model)
ローカル線形トレンドモデルは、ローカルレベルモデルを拡張し、トレンド(傾き)を含めたモデルです。
レベルの方程式:
トレンドの方程式:
観測方程式:
ここで、
このモデルは、レベルとトレンドの両方が時間とともに変化する時系列データに適しています。例えば、経済成長率や人口推移などの長期的なトレンドを持つデータの分析に有用です。
季節性モデル(Seasonal Model)
季節性モデルは、定期的に繰り返すパターンを持つ時系列データを扱うためのモデルです。
レベルの方程式:
季節性の方程式:
観測方程式:
ここで、
このモデルは、季節性を持つ時系列データ(例:月次販売データ、四半期ごとの経済指標など)に適しています。観光客数の変動や小売業の売上高など、年間を通じて周期的なパターンを示すデータの分析に有効です。
statsmodelsの
UnobservedComponentsクラスPythonのstatsmodelsライブラリは、上記で紹介した基本的な状態空間モデルを簡単に実装できる機能を提供しています。
UnobservedComponentsは、状態空間モデルを用いて時系列データの隠れた状態を推定するためのクラスです。カルマンフィルタを内部で使用して、観測データから隠れた状態をリアルタイムで推定します。モデルの定義
UnobservedComponentsを使用して、データに対するモデルを定義します。モデルには、ローカルレベル、ローカル線形トレンド、季節性などの成分を含めることができます。フィッティング
fit()メソッドを呼び出して、モデルをデータにフィットさせます。この過程で、カルマンフィルタが使用され、状態の推定が行われます。フィルタリング
filtered_stateはカルマンフィルタによって推定された状態を表します。カルマンフィルタは、観測データに基づいて隠れた状態をリアルタイムで推定するアルゴリズムであり、filtered_stateはその結果です。スムージング
smoothed_stateを使用して、全データを考慮した状態の推定を取得します。これは過去と未来の情報を考慮したより正確な推定です。予測
get_forecast()メソッドを使用して、将来の値を予測します。フィルタリングされた状態を基に予測が行われます。簡単な時系列データの分析例
ここでは、ローカルレベルモデルを使用して、簡単な時系列データを分析する例を示します。
Plain textCopy to clipboardOpen code in new windowEnlighterJS 3 Syntax Highlighterimport numpy as npimport pandas as pdimport statsmodels.api as smimport matplotlib.pyplot as plt# データの生成np.random.seed(12345)nobs = 200true_state = np.cumsum(np.random.normal(size=nobs))observed = true_state + np.random.normal(scale=0.5, size=nobs)# モデルの定義と推定mod = sm.tsa.UnobservedComponents(observed, 'local level')res = mod.fit()# 結果の表示print(res.summary())# フィルタリングされた状態の取得state_estimates = res.filtered_state[0]# プロットplt.figure(figsize=(12,6))plt.plot(observed, label='Observed')plt.plot(true_state, label='True State')plt.plot(state_estimates, label='Estimated State')plt.legend()plt.title('Local Level Model: True vs Estimated State')plt.show()import numpy as np import pandas as pd import statsmodels.api as sm import matplotlib.pyplot as plt # データの生成 np.random.seed(12345) nobs = 200 true_state = np.cumsum(np.random.normal(size=nobs)) observed = true_state + np.random.normal(scale=0.5, size=nobs) # モデルの定義と推定 mod = sm.tsa.UnobservedComponents(observed, 'local level') res = mod.fit() # 結果の表示 print(res.summary()) # フィルタリングされた状態の取得 state_estimates = res.filtered_state[0] # プロット plt.figure(figsize=(12,6)) plt.plot(observed, label='Observed') plt.plot(true_state, label='True State') plt.plot(state_estimates, label='Estimated State') plt.legend() plt.title('Local Level Model: True vs Estimated State') plt.show()import numpy as np import pandas as pd import statsmodels.api as sm import matplotlib.pyplot as plt # データの生成 np.random.seed(12345) nobs = 200 true_state = np.cumsum(np.random.normal(size=nobs)) observed = true_state + np.random.normal(scale=0.5, size=nobs) # モデルの定義と推定 mod = sm.tsa.UnobservedComponents(observed, 'local level') res = mod.fit() # 結果の表示 print(res.summary()) # フィルタリングされた状態の取得 state_estimates = res.filtered_state[0] # プロット plt.figure(figsize=(12,6)) plt.plot(observed, label='Observed') plt.plot(true_state, label='True State') plt.plot(state_estimates, label='Estimated State') plt.legend() plt.title('Local Level Model: True vs Estimated State') plt.show()このコードは、ローカルレベルモデルを使用して、観測データから真の状態を推定します。プロットを見ることで、モデルが観測データからノイズを除去し、真の状態をどの程度正確に推定できているかを視覚的に確認することができます。
以下、実行結果です。
RUNNING THE L-BFGS-B CODE * * * Machine precision = 2.220D-16 N = 2 M = 10 At X0 0 variables are exactly at the bounds At iterate 0 f= 2.27338D+00 |proj g|= 2.02876D-01 At iterate 5 f= 1.62080D+00 |proj g|= 5.21325D-02 At iterate 10 f= 1.61879D+00 |proj g|= 5.11060D-06 * * * Tit = total number of iterations Tnf = total number of function evaluations Tnint = total number of segments explored during Cauchy searches Skip = number of BFGS updates skipped Nact = number of active bounds at final generalized Cauchy point Projg = norm of the final projected gradient F = final function value * * * N Tit Tnf Tnint Skip Nact Projg F 2 10 19 1 0 0 5.111D-06 1.619D+00 F = 1.6187873637315064 CONVERGENCE: NORM_OF_PROJECTED_GRADIENT_<=_PGTOL Unobserved Components Results ============================================================================== Dep. Variable: y No. Observations: 200 Model: local level Log Likelihood -323.757 Date: Sun, 22 Sep 2024 AIC 651.515 Time: 13:55:51 BIC 658.102 Sample: 0 HQIC 654.181 - 200 Covariance Type: opg ==================================================================================== coef std err z P>|z| [0.025 0.975] ------------------------------------------------------------------------------------ sigma2.irregular 0.1482 0.120 1.240 0.215 -0.086 0.383 sigma2.level 1.2338 0.224 5.505 0.000 0.795 1.673 =================================================================================== Ljung-Box (L1) (Q): 0.00 Jarque-Bera (JB): 0.93 Prob(Q): 0.97 Prob(JB): 0.63 Heteroskedasticity (H): 0.88 Skew: 0.15 Prob(H) (two-sided): 0.61 Kurtosis: 2.85 ===================================================================================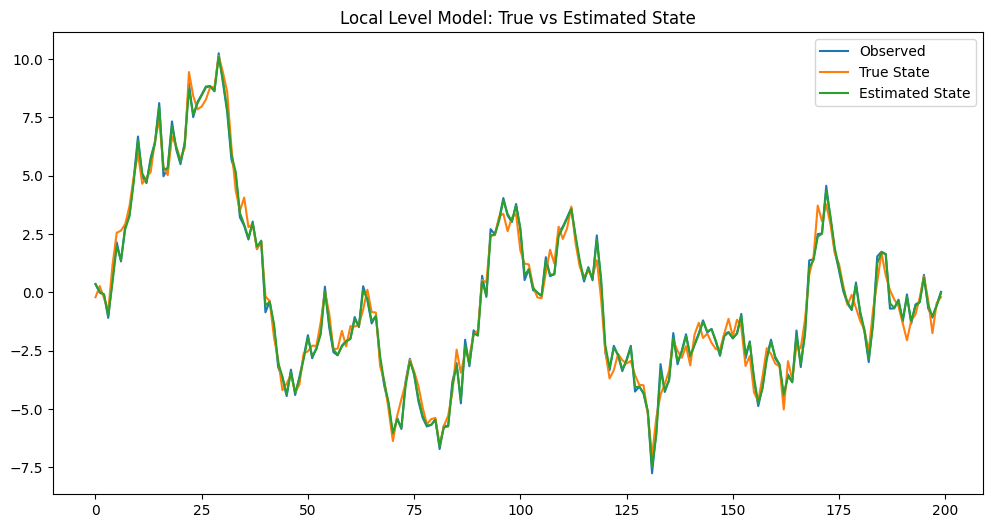
スムージング(level.smoothed)
- 全データを使用して、各時点での状態を最適に推定します。
- 過去と未来の情報を考慮して、より正確な推定を行います。
フィルタリング(filtered_state)
- 各時点までのデータのみを使用して状態を推定します。
- リアルタイムでの推定に近く、未来の情報は考慮されません。
予測を行う際には、フィルタリングされた状態を使用します。予測のロジックは以下の通りです。
- 状態の推定: ローカルレベルモデルを使用して、観測データに基づいて状態を推定します。
- フィルタリング: 各時点までのデータを使用して、状態をリアルタイムで推定します。
- 予測: フィルタリングされた状態を基に、将来の値を予測します。予測は、モデルが捉えたトレンドや変動を延長する形で行われます。
このプロセスにより、観測データに基づいて将来の値を予測し、その予測の信頼性を評価することができます。
以下、コード例です。
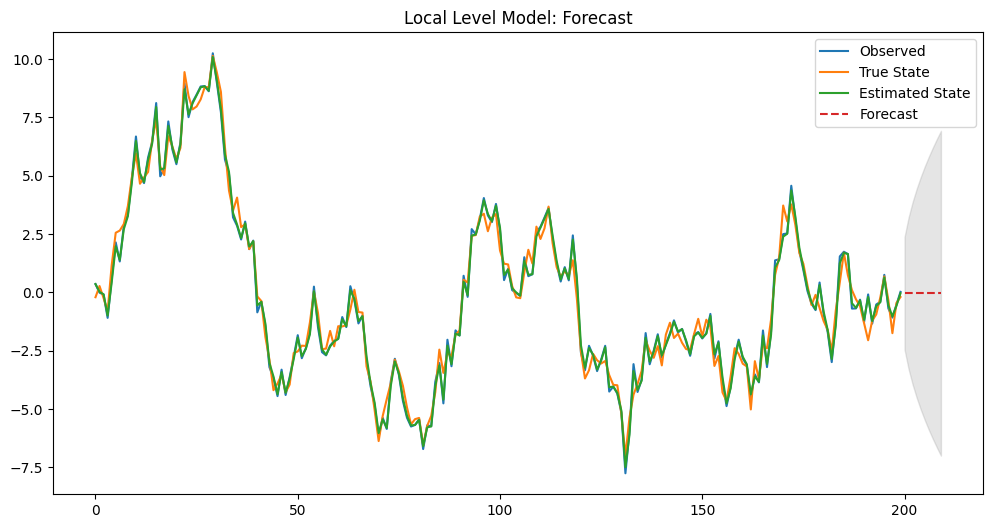
Plain textCopy to clipboardOpen code in new windowEnlighterJS 3 Syntax Highlighter# 予測の実行forecast = res.get_forecast(steps=10)forecast_index = np.arange(len(observed), len(observed) + 10)forecast_values = forecast.predicted_meanforecast_conf_int = forecast.conf_int()# 結果の表示print(forecast_values)print(forecast_conf_int)# DataFrameに変換forecast_conf_int_df = pd.DataFrame(forecast_conf_int)# プロットplt.figure(figsize=(12, 6))plt.plot(observed, label='Observed')plt.plot(true_state, label='True State')plt.plot(state_estimates, label='Estimated State')plt.plot(forecast_index, forecast_values, label='Forecast', linestyle='--')plt.fill_between(forecast_index,forecast_conf_int_df.iloc[:, 0],forecast_conf_int_df.iloc[:, 1], color='gray', alpha=0.2)plt.legend()plt.title('Local Level Model: Forecast')plt.show()# 予測の実行 forecast = res.get_forecast(steps=10) forecast_index = np.arange(len(observed), len(observed) + 10) forecast_values = forecast.predicted_mean forecast_conf_int = forecast.conf_int() # 結果の表示 print(forecast_values) print(forecast_conf_int) # DataFrameに変換 forecast_conf_int_df = pd.DataFrame(forecast_conf_int) # プロット plt.figure(figsize=(12, 6)) plt.plot(observed, label='Observed') plt.plot(true_state, label='True State') plt.plot(state_estimates, label='Estimated State') plt.plot(forecast_index, forecast_values, label='Forecast', linestyle='--') plt.fill_between(forecast_index, forecast_conf_int_df.iloc[:, 0], forecast_conf_int_df.iloc[:, 1], color='gray', alpha=0.2) plt.legend() plt.title('Local Level Model: Forecast') plt.show()# 予測の実行 forecast = res.get_forecast(steps=10) forecast_index = np.arange(len(observed), len(observed) + 10) forecast_values = forecast.predicted_mean forecast_conf_int = forecast.conf_int() # 結果の表示 print(forecast_values) print(forecast_conf_int) # DataFrameに変換 forecast_conf_int_df = pd.DataFrame(forecast_conf_int) # プロット plt.figure(figsize=(12, 6)) plt.plot(observed, label='Observed') plt.plot(true_state, label='True State') plt.plot(state_estimates, label='Estimated State') plt.plot(forecast_index, forecast_values, label='Forecast', linestyle='--') plt.fill_between(forecast_index, forecast_conf_int_df.iloc[:, 0], forecast_conf_int_df.iloc[:, 1], color='gray', alpha=0.2) plt.legend() plt.title('Local Level Model: Forecast') plt.show()以下、実行結果です。
[-0.03391005 -0.03391005 -0.03391005 -0.03391005 -0.03391005 -0.03391005 -0.03391005 -0.03391005 -0.03391005 -0.03391005] [[-2.44694653 2.37912642] [-3.28386867 3.21604856] [-3.94565096 3.87783086] [-4.51065026 4.44283016] [-5.01193063 4.94411053] [-5.46715723 5.39933712] [-5.88708533 5.81926522] [-6.27883974 6.21101963] [-6.64742899 6.57960888] [-6.99653303 6.92871292]]