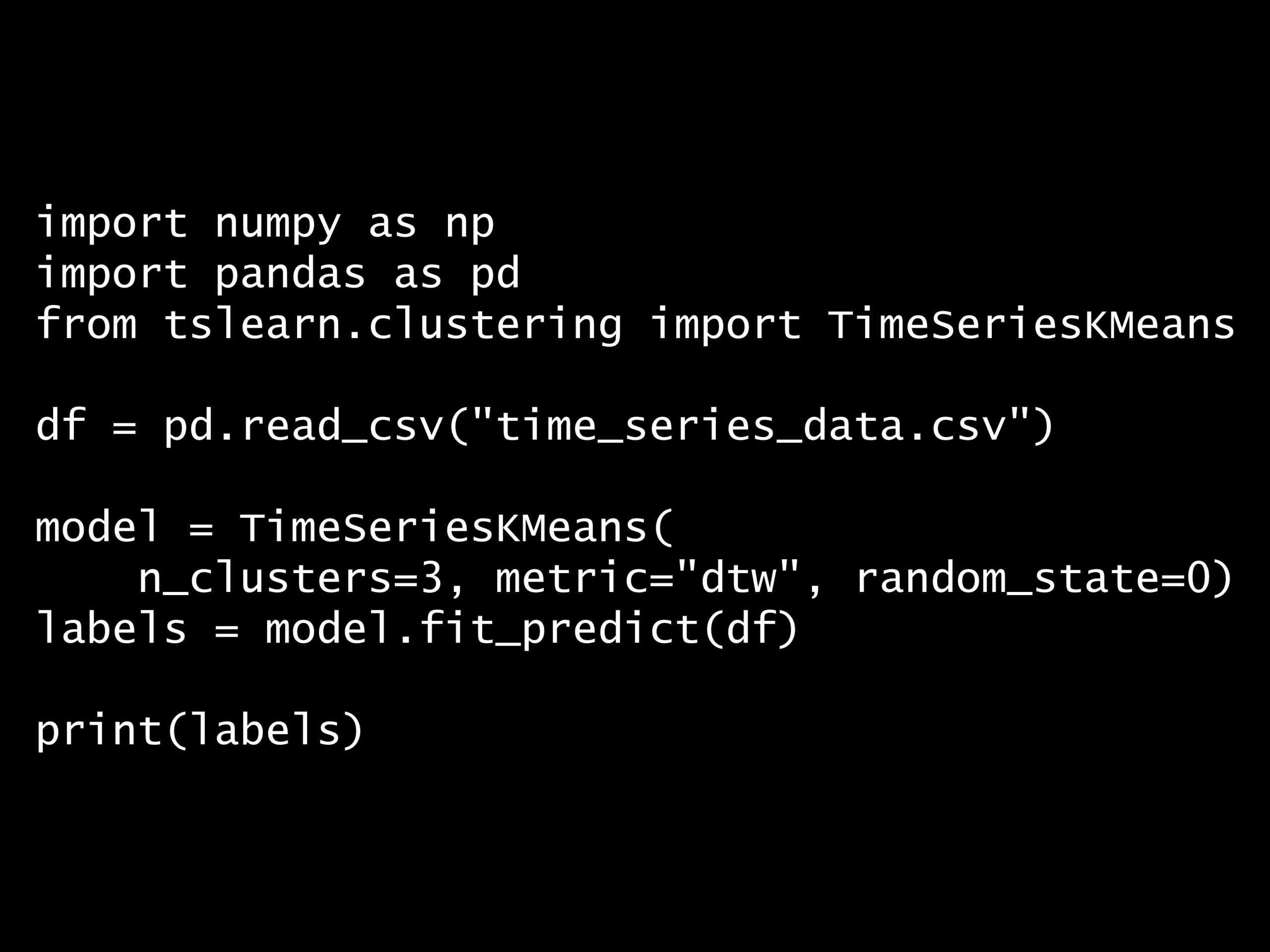
Python 時系列分析 1,000本ノック– ノック70: 時系列データのクラスタリング手法 –

問題
答え
解説

次の Python コードのクラスタリング手法は？

Python コード:

import numpy as np
import pandas as pd
from tslearn.clustering import TimeSeriesKMeans

df = pd.read_csv("time_series_data.csv")

model = TimeSeriesKMeans(
    n_clusters=3, metric="dtw", random_state=0)
labels = model.fit_predict(df)

print(labels)

回答の選択肢:

(A) DBSCANクラスタリング法
(B) 階層型クラスタリング法
(C) 動的時間伸縮法
(D) スペクトルクラスタリング法

出力例:

[1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 2 2 2 2 2 2
 2 2 2 0 0 0 0 0 0 0 0 0 0]

正解: (C)

回答の選択肢:

(A) DBSCANクラスタリング法
(B) 階層型クラスタリング法
(C) 動的時間伸縮法
(D) スペクトルクラスタリング法

コードの解説

このコードは、時系列データをクラスタリングするためのものです。

import numpy as np
import pandas as pd
from tslearn.clustering import TimeSeriesKMeans

df = pd.read_csv("time_series_data.csv")

model = TimeSeriesKMeans(
    n_clusters=3, metric="dtw", random_state=0)
labels = model.fit_predict(df)

print(labels)

詳しく説明します。

time_series_data.csv というCSVファイルからデータを読み込み、PandasのDataFrameとして df に格納します。

df = pd.read_csv("time_series_data.csv")

このCSVファイルは、以下からダウンロードできます

time_series_data.csv
https://www.salesanalytics.co.jp/kaes

df には、以下のようなデータが格納されています。

     Time_0    Time_1    Time_2    Time_3    Time_4    Time_5    Time_6  \
0  3.528105  1.800314  3.957476  7.481786  7.735116  3.045444  7.900177   
1  3.766301 -1.695518 -0.540970  4.938793  1.653753  8.887242  5.172762   
2 -0.738364  0.521242  4.199319  4.310527  5.280263  1.766088  5.951348   
3 -2.613054  4.316261  1.763672  1.639644  5.332766  4.078560  3.331483   
4 -1.197308 -1.231794  3.533326  3.712586  0.462923  5.710964  7.629040   

     Time_7     Time_8     Time_9  ...    Time_90    Time_91    Time_92  \
0  6.697286   7.793562   9.821197  ...  89.193646  93.444890  92.416550   
1  5.505090  11.845884  11.961030  ...  87.414286  91.534102  91.921434   
2  5.523938   8.559849   8.803699  ...  88.743825  90.037946  96.607833   
3  4.306565   9.387546   8.680853  ...  91.134581  90.554650  91.293137   
4  7.117851   7.629893   7.384703  ...  87.940129  90.300113  94.200569   

     Time_93    Time_94    Time_95    Time_96     Time_97     Time_98  \
0  94.953278  94.712733  96.413146  96.021000  100.571741   98.253824   
1  90.663813  95.046553  94.656907  97.543581   98.647008  102.326472   
2  90.879968  93.728101  97.273783  96.195450   98.165907   97.201102   
3  89.767052  93.416325  93.477016  97.715848   99.282204  100.933157   
4  95.596044  99.392448  94.852151  94.682894   95.971532   95.963916   

      Time_99  
0   99.803979  
1  101.673056  
2   99.740112  
3  100.705104  
4   98.844290  

[5 rows x 100 columns]

df には複数の時系列データが格納されています。プロットすると以下のようになります。

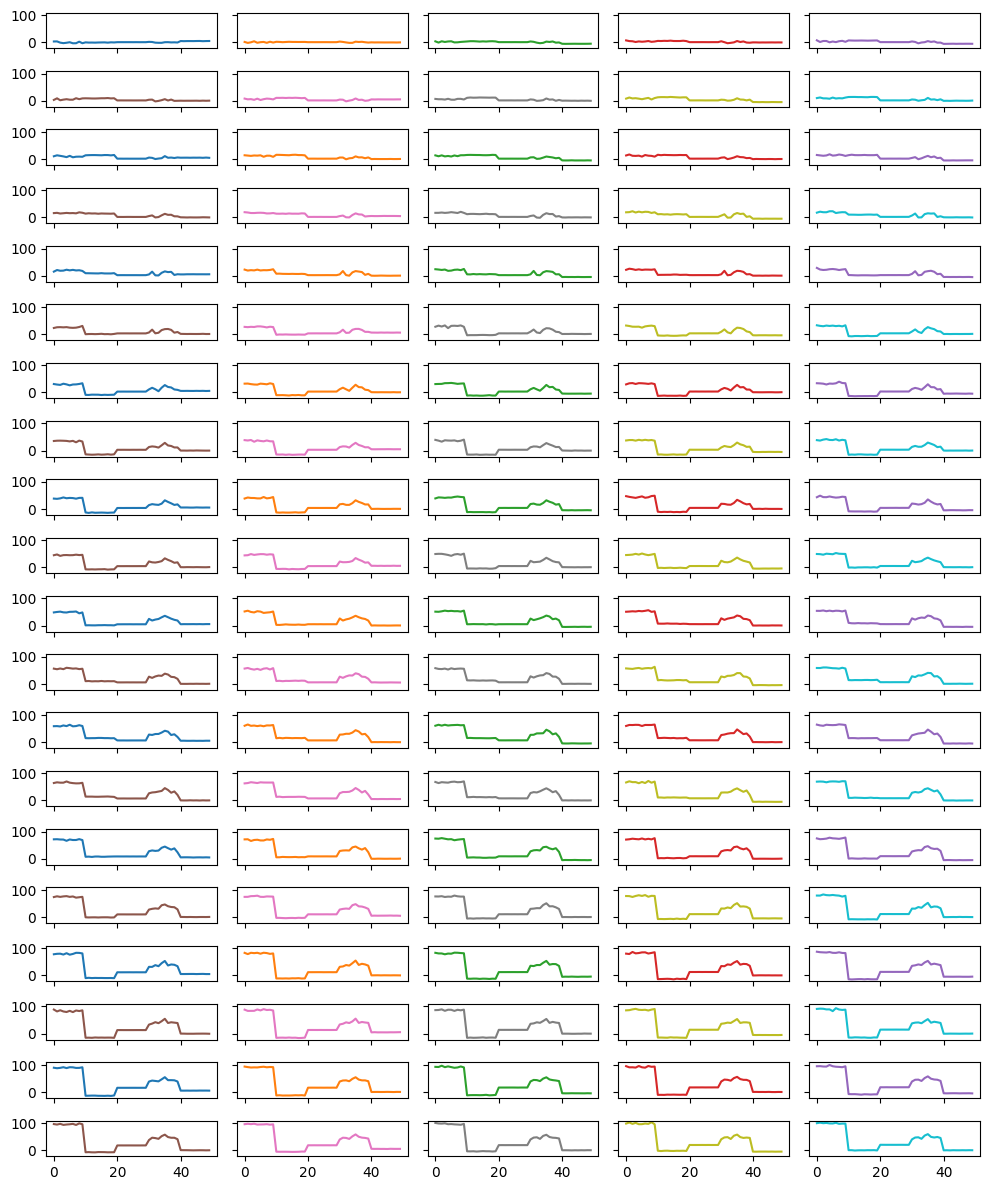
TimeSeriesKMeansのインスタンスを作成します。

model = TimeSeriesKMeans(
    n_clusters=3, metric="dtw", random_state=0)

n_clusters=3は3つのクラスタに分けることを指定し、metric="dtw"は動的時間伸縮法（DTW）を距離計算に使用することを示しています。random_state=0は結果の再現性を確保するための乱数シードを設定しています。

fit_predictメソッドを使用して、データdfの複数の時系列データをクラスタリングし、各データポイントがどのクラスタに属するかを示すラベルをlabelsに格納します。

labels = model.fit_predict(df)

各時系列データがどのクラスタに属するかを示すラベルを出力します。

print(labels)

[1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 2 2 2 2 2 2
 2 2 2 0 0 0 0 0 0 0 0 0 0]

時系列クラスタリングと動的時間伸縮法 (Dynamic Time Warping, DTW)

時系列クラスタリングとは、時系列データをグループ化する手法の一つです。時系列データは、時間の経過とともに観測されたデータポイントの集合であり、株価、気温、センサーデータなど、さまざまな分野で見られます。時系列クラスタリングの目的は、似たようなパターンを持つ時系列データを同じグループにまとめることです。

この手法は、データのパターンやトレンドを理解し、異常検知や予測モデルの構築に役立ちます。時系列クラスタリングには、動的時間伸縮法（DTW）など、時系列データの特性を考慮したさまざまな手法があります。これにより、データの時間的な変動を考慮しながら、より正確なクラスタリングが可能になります。

動的時間伸縮法 (Dynamic Time Warping, DTW) は、時系列データ間の類似性を測定するための手法です。DTWは、2つの時系列データの間の距離を計算する際に、時間軸の伸縮を許可することで、異なる速度で進行するパターンを比較することができます。これにより、例えば、異なる速度で発音された同じ単語の音声データや、異なるペースで行われた同じ動作のセンサーデータなどを効果的に比較することができます。

DTWは、動的計画法を用いて、2つの時系列データの間の最適なマッチングを見つけることで、最小の累積距離を計算します。このプロセスでは、各データポイントがどのようにマッチングされるかを決定するためのコスト行列を構築し、最小コストのパスを見つけます。この最小コストのパスが、2つの時系列データの間のDTW距離となります。

Python tslearnを利用したDTWクラスタリング

動的時間伸縮法 (Dynamic Time Warping, DTW) を用いた時系列データのクラスタリングをPythonで実装する方法を説明します。この実装では、tslearn ライブラリを使用します。

必要なライブラリのインストール

まず、tslearn ライブラリをインストールします。これは、時系列データの処理に特化したライブラリで、DTWを用いたクラスタリングもサポートしています。

pip install tslearn

実装手順

ライブラリのインポート

import numpy as np
from tslearn.clustering import TimeSeriesKMeans

必要なライブラリをインポートします。

numpy はデータの生成に、tslearn.clustering の TimeSeriesKMeans はクラスタリングに使用します。

サンプルデータの生成

np.random.seed(42)
data = np.random.rand(10, 100)

ランダムな時系列データを生成します。ここでは、10個の時系列データを生成し、それぞれ100のデータポイントを持たせます。

実務では、クラスタリング対象となる実際の多変量時系列データを読み込んでください。

モデルの定義

model = TimeSeriesKMeans(n_clusters=3, metric="dtw", random_state=0)

TimeSeriesKMeans クラスを使用して、時系列データのクラスタリングモデルを定義します。
n_clusters=3 はデータを3つのクラスタに分けることを指定しています。
metric="dtw" はDTWを距離計算に使用することを指定しています。
random_state=0 は乱数生成のシードを設定し、結果の再現性を確保します。

クラスタリングの実行

labels = model.fit_predict(data)

fit_predict メソッドを使用して、データに対してクラスタリングを実行し、各データポイントがどのクラスタに属するかを示すラベルを取得します。

結果の表示

print(labels)

各時系列データが属するクラスタのラベルを出力します。

コード全体

上記のコードをまとめると、以下となります。

import numpy as np
from tslearn.clustering import TimeSeriesKMeans

# データの生成
np.random.seed(42)
data = np.random.rand(10, 100)

# モデルの定義
model = TimeSeriesKMeans(n_clusters=3, metric="dtw", random_state=0)

# クラスタリングの実行
labels = model.fit_predict(data)

# 結果の表示
print(labels)

このコードを実行すると、各時系列データがどのクラスタに属するかを示すラベルが出力されます。

DTWを用いることで、異なる速度で進行する時系列データ間の類似性を考慮したクラスタリングが可能になります。

クラスター数の決め方

DTWクラスタリングのクラスター数を決定する方法はいくつかありますが、一般的には以下のような手法が用いられます。

エルボー法
シルエット分析

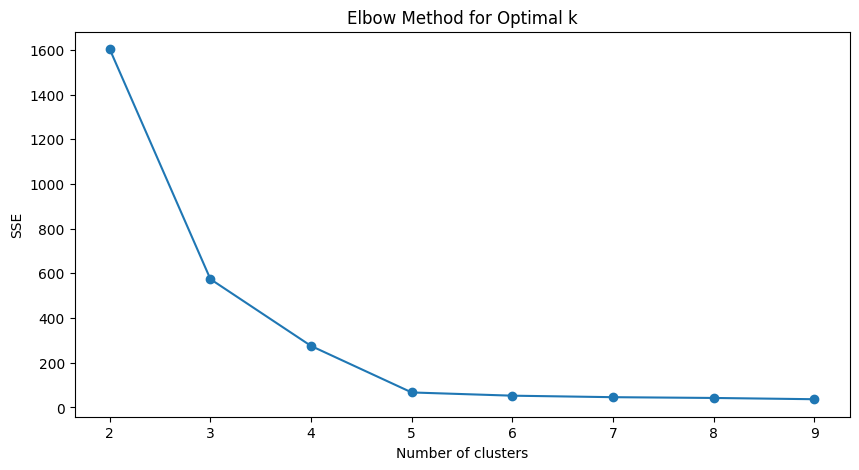
エルボー法

クラスター数を変化させながら、クラスタリングのコスト（例えば、クラスタ内の距離の総和）を計算し、その変化をプロットします。コストの減少が急激に緩やかになる点をエルボー（肘）と呼び、その点を最適なクラスター数とします。

以下、コードです。

import matplotlib.pyplot as plt
from sklearn.metrics import silhouette_score
from tslearn.clustering import TimeSeriesKMeans

# エルボー法のためのSSE計算
sse = []
for k in range(2, 10):
    model = TimeSeriesKMeans(
        n_clusters=k, 
        metric="dtw", 
        random_state=0)
    model.fit(time_series_df)
    sse.append(model.inertia_)

# エルボー法のプロット
plt.figure(figsize=(10, 5))
plt.plot(range(2, 10), sse, marker='o')
plt.title('Elbow Method for Optimal k')
plt.xlabel('Number of clusters')
plt.ylabel('SSE')
plt.show()

以下、実行結果です。

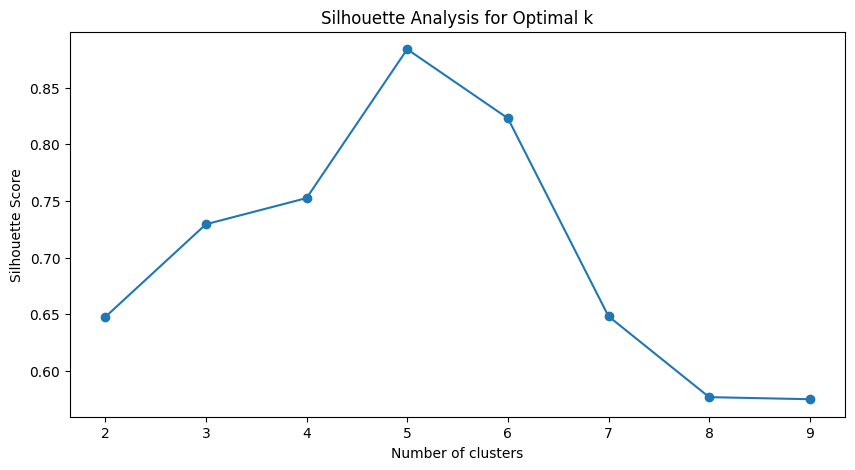
シルエット分析

各データポイントのシルエットスコアを計算し、平均シルエットスコアが最大になるクラスター数を選びます。シルエットスコアは、データポイントがどれだけ適切にクラスタに割り当てられているかを示します。

以下、コードです。

silhouette_scores = []
for k in range(2, 10):
    model = TimeSeriesKMeans(
        n_clusters=k, 
        metric="dtw", 
        random_state=0)
    labels = model.fit_predict(time_series_df)
    silhouette_avg = silhouette_score(
        time_series_df, 
        labels, 
        metric="euclidean")
    silhouette_scores.append(silhouette_avg)

# シルエット分析のプロット
plt.figure(figsize=(10, 5))
plt.plot(range(2, 10), silhouette_scores, marker='o')
plt.title('Silhouette Analysis for Optimal k')
plt.xlabel('Number of clusters')
plt.ylabel('Silhouette Score')
plt.show()

以下、実行結果です。