- 問題
- 答え
- 解説
次の Python コードのクラスタ分析の結果は?
Python コード:
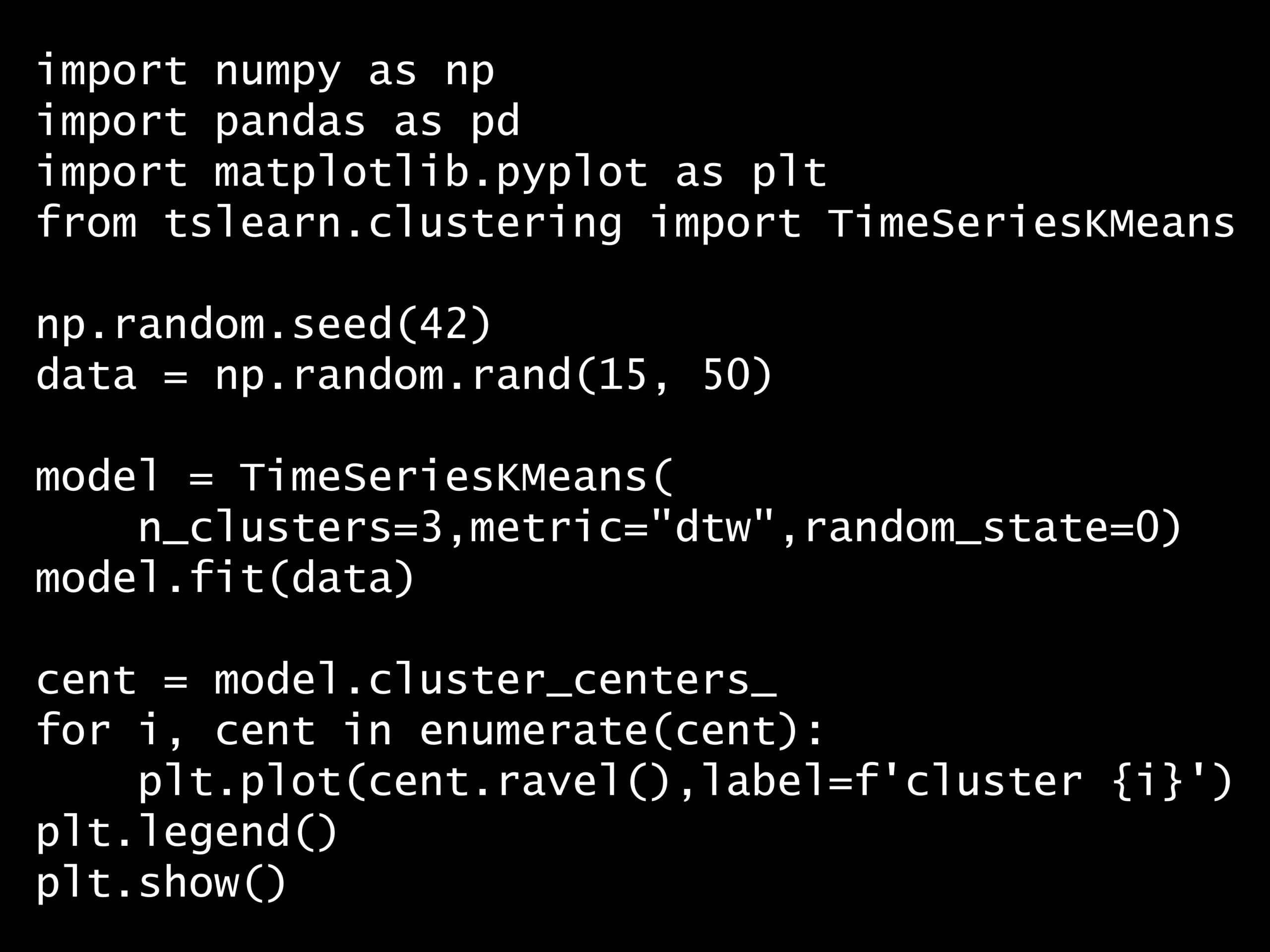
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from tslearn.clustering import TimeSeriesKMeans
np.random.seed(42)
data = np.random.rand(15, 50)
model = TimeSeriesKMeans(
n_clusters=3, metric="dtw", random_state=0)
model.fit(data)
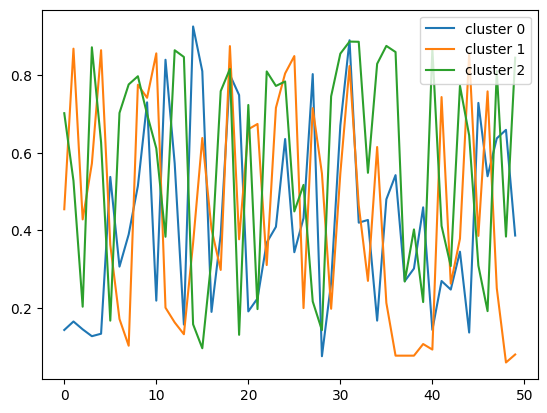
cent = model.cluster_centers_
for i, cent in enumerate(cent):
plt.plot(cent.ravel(), label=f'cluster {i}')
plt.legend()
plt.show()
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from tslearn.clustering import TimeSeriesKMeans
np.random.seed(42)
data = np.random.rand(15, 50)
model = TimeSeriesKMeans(
n_clusters=3, metric="dtw", random_state=0)
model.fit(data)
cent = model.cluster_centers_
for i, cent in enumerate(cent):
plt.plot(cent.ravel(), label=f'cluster {i}')
plt.legend()
plt.show()
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from tslearn.clustering import TimeSeriesKMeans
np.random.seed(42)
data = np.random.rand(15, 50)
model = TimeSeriesKMeans(
n_clusters=3, metric="dtw", random_state=0)
model.fit(data)
cent = model.cluster_centers_
for i, cent in enumerate(cent):
plt.plot(cent.ravel(), label=f'cluster {i}')
plt.legend()
plt.show()
回答の選択肢:
(A) 各クラスタの最小値
(B) 各クラスタの平均
(C) 各クラスタの中心との距離
(D) 各クラスタのクラスター番号