データを活用したマーケティング戦略は、ビジネスの成功に不可欠です。その中心に位置するのが、マーケティングミックスモデリング(MMM)です。
マーケティングミックスモデリング(MMM)は、過去のデータを分析する「振り返り分析」と未来のトレンドを予測する「近未来分析」の両方で有効に活用される強力なツールです。
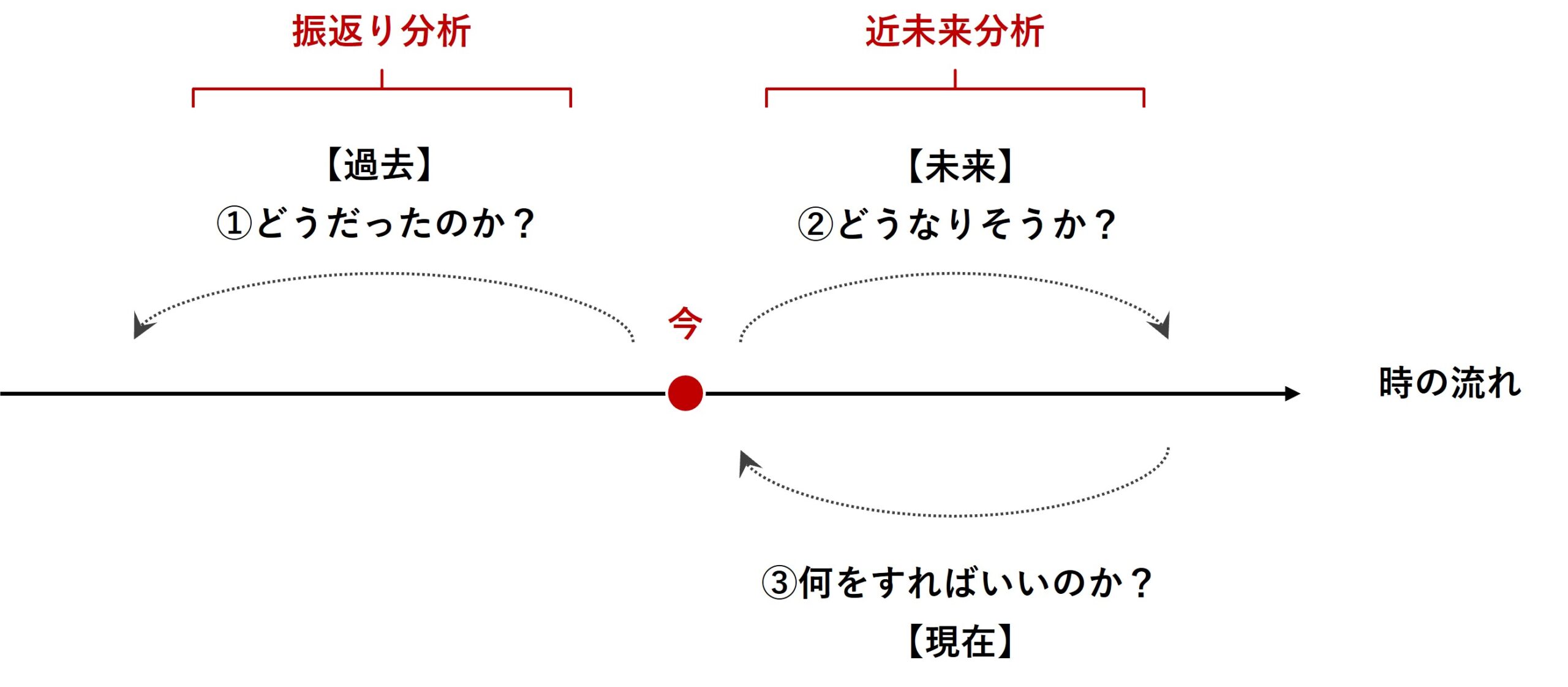
前回は、「MMMによる『振返り分析』とは?」に焦点を当て、事例を交えお話ししました。
今回は、「線形回帰系モデルでのMMM構築」というお話しを、Pythonコードを交えお話しします。
少し長いですので、単に線形回帰モデルでMMMを構築したい方は、最初の方の「一般的な線形回帰モデルでMMM」だけ読んで頂ければと思います。
それ以降は、様々な線形系のモデルでの構築方法をダラダラと解説しています。最後の方で「線形系のモデル(推定器)の自動選択」を説明していますので、そのためのフリです。
ちなみに、アドストック(キャリーオーバー効果や飽和効果)を考慮していないモデルです。アドストックに関しては、次回以降取り上げます。
Contents [hide]
- 利用するデータセット
- 処理の流れ
- 今回利用する線形系モデル
- 【補足】多重共線性(Multicollinearity)問題
- 一般的な線形回帰モデルでMMM
- 線形回帰モデルとは?
- ステップByステップでMMM構築
- 準備(モジュールとデータの読み込み)
- MMM構築
- 後処理(結果の出力)
- 処理を関数化する
- 構築する関数
- 準備(モジュールとデータの読み込み)
- MMM構築用の関数
- 後処理(結果の出力)用の関数
- 関数をpyファイルに保存し流用
- 発展的話題① – 様々な線形回帰系モデルで構築するMMM
- リッジ回帰でMMM
- リッジ回帰とは?
- 準備(モジュールとデータの読み込み)
- ハイパーパラメータをデフォルトのままMMM構築
- Optunaによるハイパーパラメータ調整しMMM構築
- ベイズリッジ回帰でMMM
- ベイズリッジ回帰とは?
- 準備(モジュールとデータの読み込み)
- ハイパーパラメータをデフォルトのままMMM構築
- Optunaによるハイパーパラメータ調整しMMM構築
- PLS回帰でMMM(パイプライン構築)
- PLS回帰とは?
- 準備(モジュールとデータの読み込み)
- ハイパーパラメータをデフォルトのままMMM構築
- Optunaによるハイパーパラメータ調整しMMM構築
- 主成分回帰でMMM(パイプライン構築)
- 主成分回帰とは?
- 準備(モジュールとデータの読み込み)
- ハイパーパラメータをデフォルトのままMMM構築
- Optunaによるハイパーパラメータ調整しMMM構築
- 発展的話題② – 線形系のモデル(推定器)の自動選択
- 準備
- モデル(もしくはパイプライン)リスト
- Optunaで自動探索&チューニング
- MMM構築
- 後処理(結果の出力)
- まとめ
利用するデータセット
以下のデータセットを前提に説明します。
- 目的変数:売上金額(Sales)
- 説明変数:TVCM、Newspaper、Webのコスト
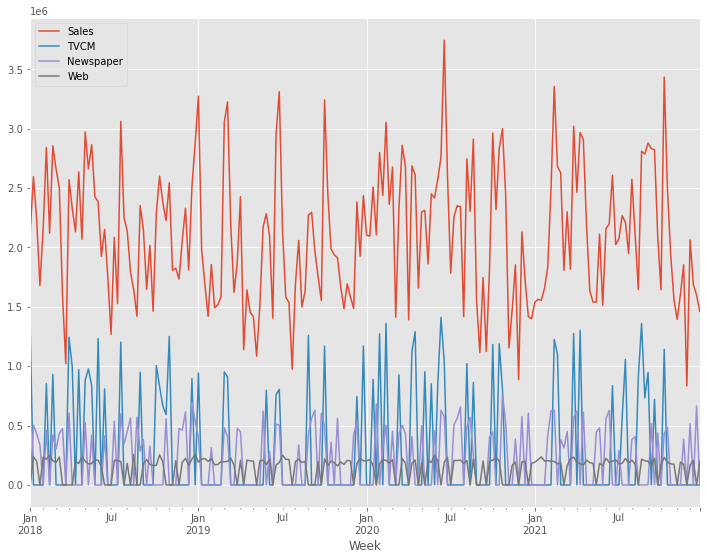
今回利用するデータセットは、以下からダウンロードできます。
目的変数は、売上金額である必要はありません。例えば、売上点数でも受注件数、問い合せ件数、予約件数でも構いません。要は、広告販促でより良い変化をさせたい何かです。
説明変数は、コストでなくても構いません。例えば、媒体の認知や接触、露出、広告のクリック、インプレッション、配信、開封などでも構いません。ただ、コスパという概念を持ち出すとき、少なくともコストデータは必要になります。
処理の流れ
以下は、簡単な処理の流れです。

- 先ず、MMMを構築します。
- 次に、売上をMMMを使い分解し、媒体別の売上貢献度を求めます。
- 最後に、売上貢献度(補正済み)を使い、媒体別のROIを計算します。
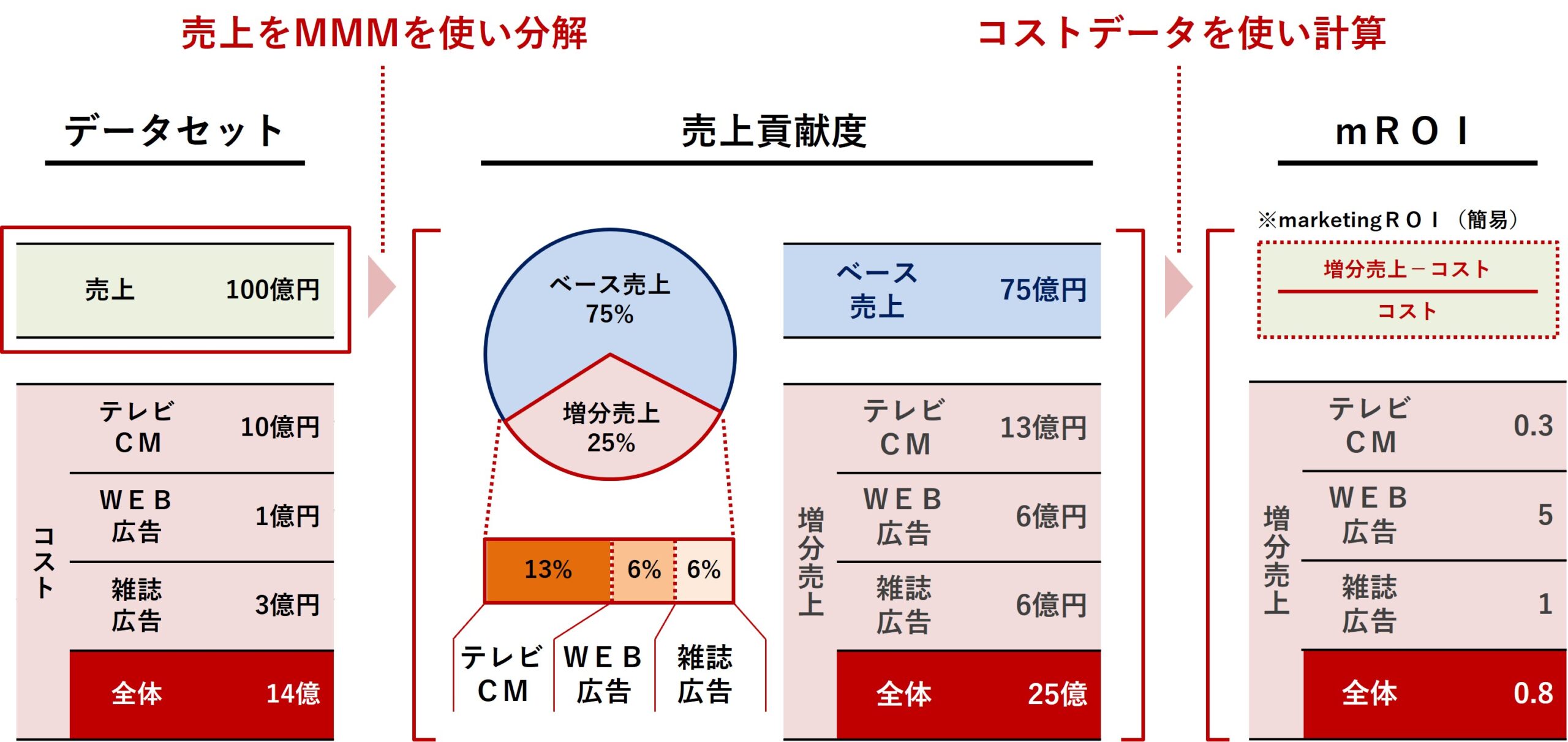
ちなみに、売上貢献度を足し合わせると売上の予測値になりますが、通常の予測値は実測値と乖離します。予測値を実測値に合わせるための補正係数を計算し、補正済み売上貢献度を計算します。
今回利用する線形系モデル
今回はPythonのscikit-learn(sklearn)ライブラリーを利用し、線形系のモデルでMMMを構築していきます。
scikit-learn(sklearn)にはたくさんの線形系のモデルがあります。
以下は、scikit-learn(sklearn)の線形回帰系のモデルの一部です(2024年1月24日現在)。
| クラス名 | 特徴 |
|---|---|
LinearRegression |
基本的な線形回帰モデル。最小二乗法を使用してパラメータを推定します。 |
Ridge |
L2正則化を加えた線形回帰(リッジ回帰)。多重共線性を扱うのに適しています。 |
Lasso |
L1正則化を加えた線形回帰。不要な特徴量の係数を0にし、スパースなモデルを作成します。 |
ElasticNet |
L1とL2の両方の正則化を組み合わせたモデル。正則化のバランスが調整可能です。 |
Lars |
最小角回帰。計算効率が良く、高次元データに適しています。 |
LassoLars |
L1正則化を使用した最小角回帰。小さいデータセットに適しています。 |
OrthogonalMatchingPursuit |
事前に定められた非ゼロ係数の数に基づいてモデルを作成します。 |
BayesianRidge |
ベイジアンリッジ回帰。事前分布を用いて正則化されます。 |
ARDRegression |
自動関連決定法(ARD)を使用したベイジアンリッジ回帰。 |
SGDRegressor |
確率的勾配降下法を使用した線形モデル。大規模なデータセットに適しています。 |
PassiveAggressiveRegressor |
オンライン学習に適したパッシブアグレッシブアルゴリズムを使用します。 |
RANSACRegressor |
外れ値に強いモデルを作成するためのRANSACアルゴリズムを使用します。 |
TheilSenRegressor |
外れ値に強く、中央値に基づく回帰を提供します。 |
HuberRegressor |
外れ値に対して頑健な回帰モデル。Huber損失を使用します。 |
QuantileRegressor |
分位数回帰を行います。データの特定の分位数に基づくモデルを作成します。 |
PLSRegression |
部分的最小2乗回帰(Partial Least Squares Regression)。高次元データの次元削減や多重共線性問題に有効です。 |
LinearRegressionは、一般的な線形回帰モデルで、俗にいう重回帰モデルで、基本となるモデルです。
大規模なデータセットでは、SGDRegressorのような計算効率が高いモデルが有利です。
外れ値が多い場合には、HuberRegressorやRANSACRegressor、QuantileRegressorが有効です。
| モデル名 | 特徴 | 主な使用シナリオ |
|---|---|---|
| HuberRegressor | 外れ値に対して頑健な回帰モデル。誤差がある閾値以下の場合は二乗誤差、以上の場合は線形誤差を使用する。 | 外れ値が含まれるデータセットや、外れ値の影響を最小限に抑えたい場合。 |
| RANSACRegressor | 外れ値を自動的に検出し、それらを除外してモデルを構築する。不均一なデータや外れ値に対して頑健。 | データに多数の外れ値が含まれる場合や、外れ値の影響を受けやすい場合。 |
| QuantileRegressor | 分位数回帰を行う。データの特定の分位数(例えば中央値)に基づいてモデルを構築する。 | データの中央傾向ではなく、特定の分位数に焦点を当てた予測をしたい場合。 |
広告販促系のデータは、お互いの相関関係が強い傾向(同じ時期に集中し広告投下など)があり、多重共線性問題が起こる可能性が低くはありません。
そのような場合には、RidgeやElasticNet、BayesianRidge 、 ARDRegressionなどのRidge(リッジ)回帰系のモデルです。
| モデル名 | 特徴 | 主な使用シナリオ |
|---|---|---|
| Ridge | L2正則化を加えた線形回帰。多重共線性の問題を緩和する。 | 予測変数間に相関があり、多重共線性が問題になる場合。 |
| ElasticNet | L1とL2の両方の正則化を組み合わせたモデル。特徴量の選択と多重共線性の緩和を同時に行う。 | 予測変数が多く、一部は重要で他は不要、または多重共線性が問題になる場合。 |
| BayesianRidge | ベイズ統計に基づいたリッジ回帰。事後分布からの推定値と不確実性の推定が可能。 | 不確実性の推定が重要で、事後分布からの洞察が求められる場合。 |
| ARDRegression | 自動関連決定法に基づいたベイジアンリッジ回帰。各係数に対して個別の正則化を行うことで、スパースな解を提供する。 | 多くの特徴量があり、その中の少数のみが重要、または不要な特徴が多い場合。 |
他には、元の説明変数に対し主成分分析を施すことで、相関関係の弱いデータに変化し線形回帰モデルを構築する主成分回帰モデル(PCAとLinearRegressionの組み合わせ)や、その親戚であるPLSRegressionがあります。
使い分けですが、多重共線性問題の可能性を考慮し、通常はRidgeor PLSRegressionがシンプルで良いかと思います。大規模なデータセットの場合には主成分分析(PCA)とSGDRegressorを組み合わせると良いかと思います。
モデルの係数などに特定の分布や条件を課す場合には、scikit-learn(sklearn)ライブラリーではなく、PyStanやPyMCなどのベイズモデリング系のライブラリーでモデル構築するといいでしょう。
今回は、以下の5つの線形系のモデルを、scikit-learn(sklearn)ライブラリーを使い構築します。
LinearRegression:一般的な線形回帰モデルRidge:L2正則化を加えた線形回帰(リッジ回帰)BayesianRidge:ベイズ統計に基づいたリッジ回帰PLSRegression:部分的最小2乗回帰(Partial Least Squares Regression)- 主成分回帰:
PCAとLinearRegressionの組み合わせ
【補足】多重共線性(Multicollinearity)問題
補足説明になります。気になる方のみ一読ください。
多重共線性(Multicollinearity)問題は、特に線形回帰モデルの文脈で発生する問題ですが、他の多くの種類の統計モデルにおいても関連があります。この問題は、モデルの説明変数間に高い相関関係が存在する場合に生じます。
多重共線性の存在は、例えば以下のような問題を引き起こす可能性があります。
- パラメータ推定の不安定性: 相関関係のある変数がモデルに含まれていると、それぞれの変数の影響を正確に推定することが困難になります。これは、小さなデータの変動が推定される係数に大きな影響を与える可能性があるためです。
- 解釈の困難さ: 多重共線性がある場合、個々の変数の影響を分離して解釈することが難しくなります。これは、変数間の相関が高いため、どの変数が目的変数に影響を与えているかを明確に特定できないためです。
- 過剰適合(Overfitting)のリスク: 相関関係のある変数を多く含むモデルは、トレーニングデータに対して過剰に適合する傾向があり、新しいデータに対する予測性能が低下する可能性があります。
- 統計的有意性の問題: 多重共線性は、変数の統計的有意性のテストに影響を与える可能性があります。特定の変数が統計的に有意であるかどうかを正しく判断することが難しくなる場合があります。
多重共線性の問題に対処するために次のような手法が一般的に用いられます。
- 変数の選択: 相関関係のある変数の一部をモデルから除外することで、多重共線性を減少させることができます。
- 正則化技法の使用: リッジ回帰(Ridge)やラッソ回帰(Lasso)のような正則化技法は、多重共線性の問題を緩和するのに役立ちます。
- 主成分分析(PCA): 変数間の相関を取り除くために、主成分分析を用いてデータの次元削減を行うことができます。
多重共線性の問題は、特に予測モデリングや因果関係の分析を行う際に考慮する必要があります。正しいモデル選択と変数処理は、ビジネス上の意思決定におけるデータ駆動型のアプローチの信頼性と有効性を高めるために重要です。
一般的な線形回帰モデルでMMM
scikit-learn(sklearn)ライブラリーのLinearRegression(一般的な線形回帰モデル)でMMMを構築します。
線形回帰モデルとは?
scikit-learn(sklearn)ライブラリーにおける LinearRegression は、一般的な線形回帰モデルを実装しています。
このモデルは、目的変数と一つ以上の説明変数の間の線形関係をモデリングするために使用されます。
- 基本的な仮定: 線形回帰は、目的変数と説明変数間に線形関係があるという仮定に基づいています。
- 最小二乗法: このモデルは、観測値とモデルによる予測値の差(誤差)の二乗和を最小にするように係数を推定します。
- 解釈の容易さ: 線形回帰モデルは、その係数(重み)が直接的な解釈を可能にするため、ビジネスの文脈での意思決定に役立ちます。
- 正則化なし:
LinearRegressionは正則化を適用せず、データに最も適合する線形関係を見つけます。ただし、多重共線性のような問題がある場合には、他の正則化を含む回帰手法(例:Ridge、Lasso)を検討する必要があります。
LinearRegression モデルは、scikit-learn で簡単に実装でき、データの前処理からモデルのトレーニング、予測までのプロセスが直感的で分かりやすいです。ただし、モデルの適用前にデータの特性を十分に理解し、必要な前処理(例:欠損値の処理、カテゴリ変数のエンコーディング)を行うことが重要です。
ステップByステップでMMM構築
準備(モジュールとデータの読み込み)
先ずは、必要なモジュールを読み込みます。
以下、コードです。
import numpy as np
import pandas as pd
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
from sklearn.metrics import mean_absolute_error
from sklearn.metrics import mean_absolute_percentage_error
from sklearn.metrics import r2_score
import warnings
warnings.simplefilter('ignore')
import matplotlib.pyplot as plt
plt.style.use('ggplot') #グラフスタイル
plt.rcParams['figure.figsize'] = [12, 7] #グラフサイズ
plt.rcParams['font.size'] = 9 #フォントサイズ
import numpy as np:- NumPyは、Pythonで数値計算を行うための基本的なライブラリで、配列や行列などの数値データの操作に使用されます。
npという省略形で使えるようにしています。
import pandas as pd:- Pandasは、データ分析を容易にする機能を提供するライブラリで、特にデータフレームという形式でデータを扱う際に便利です。
pdという省略形で使えるようにしています。
from sklearn.linear_model import LinearRegression:- scikit-learnから線形回帰モデル(
LinearRegression)をインポートしています。 - 線形回帰は、与えられたデータに基づいて、出力と特徴の関係をモデリングするために使用される基本的な機械学習アルゴリズムです。
- scikit-learnから線形回帰モデル(
from sklearn.metrics import mean_squared_error,mean_absolute_error, mean_absolute_percentage_error, r2_score:- ここでは、モデルのパフォーマンス評価のために様々なメトリクスをインポートしています。
- 平均二乗誤差 (MSE: Mean Squared Error):
- 予測値と実際の値の差の平方の平均。
- 大きな誤差に対して敏感。
- 平均絶対誤差 (MAE: Mean Absolute Error):
- 予測値と実際の値の絶対差の平均。
- 外れ値の影響を受けにくい。
- 平均絶対パーセンテージ誤差 (MAPE: Mean Absolute Percentage Error):
- 予測値と実際の値の差の割合の平均。
- 相対的な誤差を表し、スケールの異なるデータセット間の比較に適している。
- 決定係数 (R²スコア: Coefficient of Determination):
- モデルが目的変数の変動をどれだけ説明しているかを示す。
- 1に近いほど良いモデル。0以下は最悪の場合。
import warnings&warnings.simplefilter('ignore'):- Pythonで発生する警告を制御するためにwarningsライブラリを使用します。
- ここでは、
simplefilter('ignore')を使って、すべての警告を無視するように設定しています。 - これは、特に非推奨の機能に関連する警告を非表示にするのに役立ちます。
import matplotlib.pyplot as plt& スタイル、サイズ設定:- Matplotlibは、Pythonでグラフを作成するためのライブラリです。
pltという省略形でインポートされます。- その後、グラフのスタイル(
'ggplot')、図のサイズ、フォントサイズを設定しています。 - これらの設定はグラフの外観をカスタマイズするために使用されます。
次に、データセットを読み込みます。
以下、コードです。
# データセット読み込み
dataset = 'https://www.salesanalytics.co.jp/4zdt'
df = pd.read_csv(
dataset,
parse_dates=['Week'],
index_col='Week',
)
# 説明変数Xと目的変数yに分解
X = df.drop(columns=['Sales'])
y = df['Sales']
- データセット読み込み:
dataset = 'https://www.salesanalytics.co.jp/4zdt': ここで、データセットのURLが指定されています。df = pd.read_csv(...): この行では、Pandasライブラリのread_csv関数を使用して、指定されたURLからデータセットを読み込んでいます。この関数は、CSV形式(カンマ区切りの値)のデータを読み込むのに広く使われています。parse_dates=['Week']: この引数は、’Week’列を日付型のデータとして解析するように指示しています。index_col='Week': この引数は、’Week’列をデータフレームのインデックス(行のラベル)として使用するように指示しています。
- 説明変数Xと目的変数yに分解:
X = df.drop(columns=['Sales']): ここでは、dropメソッドを使用して’Sales’列を除外し、残りの列を説明変数Xとして保持しています。dropは指定された列をデータフレームから削除するために使われます。y = df['Sales']: この行では、’Sales’列を目的変数yとして抽出しています。目的変数は、モデルによって予測されるべき変数であり、このケースでは売上データと思われます。
目的変数y(売上)をプロットします。
以下、コードです。
y.plot() plt.show()
以下、実行結果です。
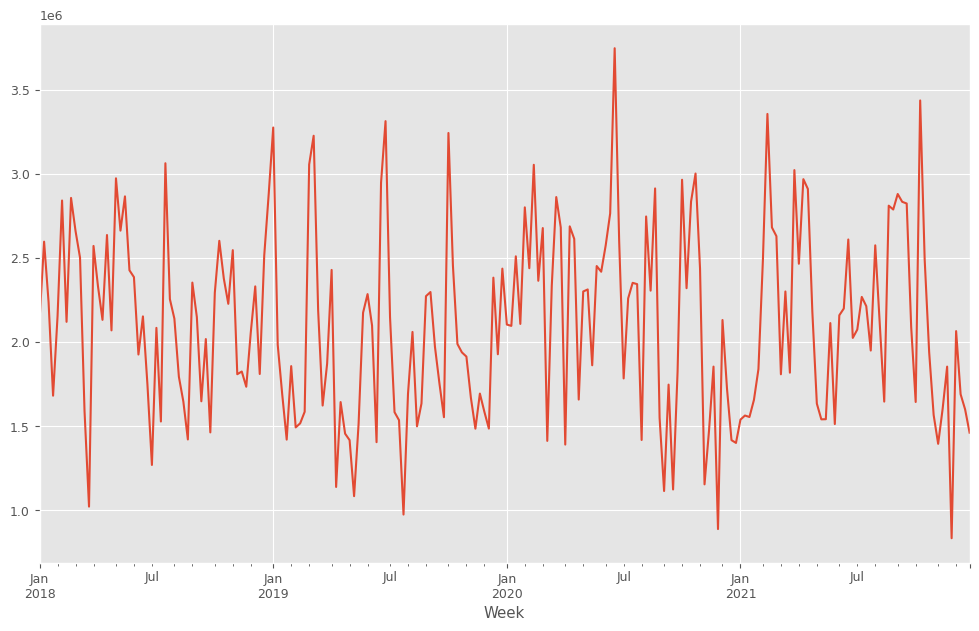
y.plot():y(目的変数)を折れ線グラフで表示します。plot()はPandasのデフォルトのグラフ化するためのプロット機能です。plt.show(): 作成されたグラフを画面に出力します。
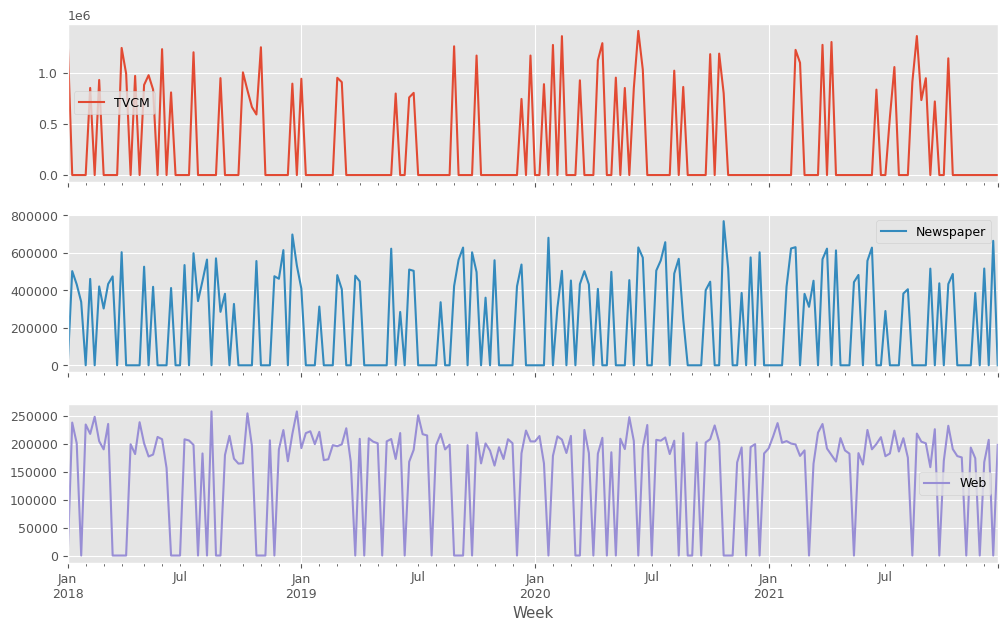
説明変数X(各メディアのコスト)をまとめてプロットします。
以下、コードです。
X.plot(subplots=True) plt.show()
X.plot(subplots=True):X(説明変数)を折れ線グラフで表示します。subplots=Trueは、Xの各列(各媒体)を別々のサブプロットとして表示することを意味します。これにより、各説明変数の動きを個別に確認できます。plt.show(): 作成されたグラフを画面に出力します。
以下、実行結果です。
MMM構築
線形回帰モデルでMMMを構築します。
以下、コードです。
#
# MMMの構築
#
# インスタンス
MMM = LinearRegression()
# 学習
MMM.fit(X, y)
# 予測
pred = pd.DataFrame(
MMM.predict(X),
index=X.index,
columns=['y'],
)
# 精度指標
print('RMSE:\n',
np.sqrt(mean_squared_error(y, pred)))
print('MAE:\n',
mean_absolute_error(y, pred))
print('MAPE:\n',
mean_absolute_percentage_error(y, pred))
print('R2:\n',
r2_score(y, pred))
- インスタンス化:
MMM = LinearRegression():LinearRegressionクラスのインスタンスを作成します。- これは、線形回帰モデルを表しており、データから線形関係を学習するために使用されます。
- モデルの学習:
MMM.fit(X, y):fitメソッドを使用して、説明変数Xと目的変数yに基づいてモデルを学習させます。- このプロセスでは、モデルは
Xとyの間の関係を見つけ出すために、内部パラメータを調整します。
- 予測の生成:
pred = pd.DataFrame(...):predictメソッドを使用して、学習済みのモデルを使ってXに基づいた予測を生成します。- その後、この予測をPandasのデータフレームに変換し、
X.indexをインデックスとして設定し、列名を'y'としています。
- 精度指標の計算:
- ここでは、実際の値
yと予測値predを用いて、以下の精度指標を計算しています。- 平均二乗誤差の平方根 (Root Mean Squared Error):
- 予測値と実際の値の差の平方の平均の平方根。
- 大きな誤差に対して敏感。
- 平均絶対誤差 (MAE: Mean Absolute Error):
- 予測値と実際の値の絶対差の平均。
- 外れ値の影響を受けにくい。
- 平均絶対パーセンテージ誤差 (MAPE: Mean Absolute Percentage Error):
- 予測値と実際の値の差の割合の平均。
- 相対的な誤差を表し、スケールの異なるデータセット間の比較に適している。
- 決定係数 (R²スコア: Coefficient of Determination):
- モデルが目的変数の変動をどれだけ説明しているかを示す。
- 1に近いほど良いモデル。0以下は最悪の場合。
- 平均二乗誤差の平方根 (Root Mean Squared Error):
- ここでは、実際の値
以下、実行結果です。
RMSE: 284667.75543375366 MAE: 237679.0368036913 MAPE: 0.12129533117151893 R2: 0.7400400171566187
- RMSE (Root Mean Squared Error: 平均二乗誤差の平方根):
- 値: 284,667.76
- この値は、モデルの予測値と実際の値との差の平均的な大きさを示しています。
- 数値が大きいほど、誤差が大きいことを意味します。
- MAE (Mean Absolute Error: 平均絶対誤差):
- 値: 237,679.04
- MAEは、予測値と実際の値との絶対差の平均を示しています。
- RMSEよりも外れ値の影響を受けにくく、こちらも値が大きいほど誤差が大きいことを意味します。
- MAPE (Mean Absolute Percentage Error: 平均絶対パーセンテージ誤差):
- 値: 12.13%
- 予測値が実際の値から平均して約12.13%ずれていることを示しています。
- この指標はパーセンテージで表されるため、結果の相対的な大きさを理解しやすいです。
- R² (R squared: 決定係数):
- 値: 0.740
- モデルがデータの約74%の変動を説明していることを示しています。R²の値が1に近いほど、モデルがデータに適合していることを意味します。
- 0.74は比較的高い値であり、モデルがデータをかなりうまく説明していることを示していますが、まだ改善の余地があります。
MMMの予測値(predicted)と実測値(actual)の推移をプロットします。
以下、コードです。
#
# グラフ化
#
fig, ax = plt.subplots()
ax.plot(y.index,
y.values,
label="actual")
ax.plot(y.index,
pred.y.values,
label="predicted",
linestyle="dotted",
lw=2)
ax.set_ylim(0, 4e6)
plt.legend()
plt.show()
- グラフの準備:
fig, ax = plt.subplots(): この行では、グラフを描画するための図(fig)と座標軸(ax)を作成しています。
- 実際の値のプロット:
ax.plot(y.index, y.values, label="actual"):plotメソッドを使用して、実際の値(y.values)をプロットしています。y.indexはx軸に、y.valuesはy軸に対応しています。label="actual"は、この線が実際の値を表していることを示すラベルです。
- 予測値のプロット:
ax.plot(y.index, pred.y.values, label="predicted", linestyle="dotted", lw=2): 予測値も同様にプロットしていますが、linestyle="dotted"(点線スタイル)とlw=2(線の太さ)のオプションで視覚的に区別しています。- これにより、予測値と実際の値を比較しやすくなります。
- y軸の範囲設定:
ax.set_ylim(0, 4e6): y軸の範囲を0から400万までに設定しています。- これにより、グラフ上でのデータの表示範囲を調整しています。
- 凡例の表示とグラフの表示:
plt.legend(): 凡例を表示するためのコマンドです。これにより、どの線が「実際の値」でどの線が「予測値」を示しているかがわかります。plt.show(): 最終的にグラフを画面に表示するコマンドです。
以下、実行結果です。
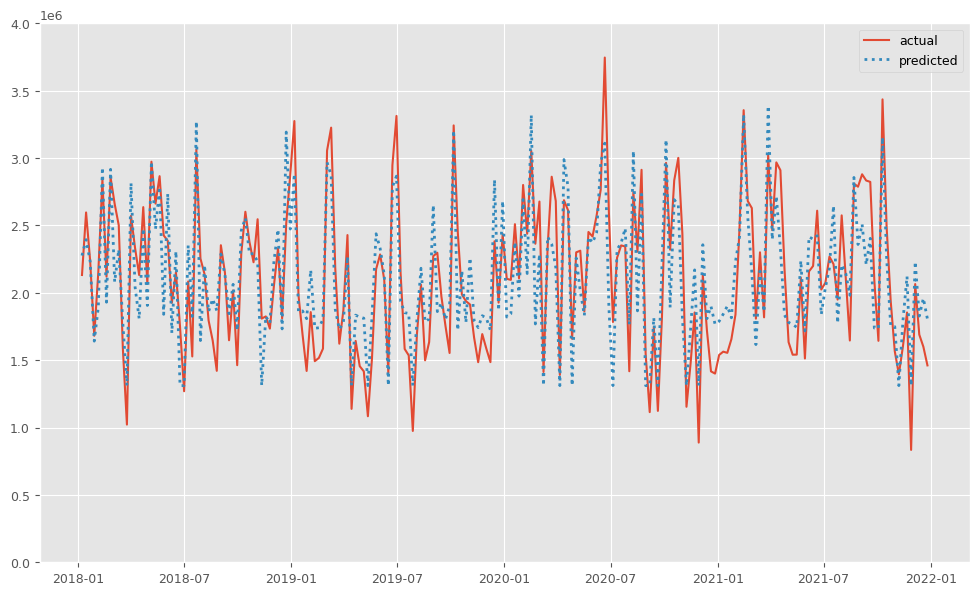
予測値と実測値のずれは、後で補正します。そのため、予測値の精度は高い必要があります。例えば、
後処理(結果の出力)
予測値を元に、貢献度を算定します。
以下、コードです。
#
# 貢献度の算定
#
# 各媒体による売上の予測
## 値がすべて0の説明変数
X_ = X.copy()
X_.iloc[:,:]=0
# Baseの予測
base = MMM.predict(X_)
pred['Base'] = base
## 媒体
for i in range(len(X.columns)):
X_.iloc[:,:]=0
X_.iloc[:,i]=X.iloc[:,i]
pred[X.columns[i]] = MMM.predict(X_) - base
# 予測値の補正
correction_factor = y.div(pred.y, axis=0) #補正係数
pred_adj = pred.mul(correction_factor, axis=0) #補正後の予測値
# 各媒体の貢献度だけ抽出
contribution = pred_adj.drop(columns=['y'])
print(contribution)
# グラフ化
ax = contribution.plot.area(
ylabel='Sales',
xlabel='Week',
)
handles, labels = ax.get_legend_handles_labels()
ax.legend(reversed(handles), reversed(labels))
ax.set_ylim(0, 4e6)
plt.show()
- 貢献度の算定:
X_ = X.copy(): まず、元の説明変数データセットXのコピーを作成します。X_.iloc[:,:]=0: すべての値を0に設定し、基準(ベースライン)のシナリオを作成します。
- 基準予測の生成:
base = MMM.predict(X_): すべての媒体の効果を除外した基準状態(ベースライン)での売上予測を行います。pred['Base'] = base: この基準予測をpredデータフレームに追加します。
- 各媒体の貢献度計算:
forループを使用して、各媒体の影響を一つずつ追加しながら予測を行います。X_.iloc[:,:]=0で他の媒体の効果を除外し、X_.iloc[:,i]=X.iloc[:,i]で特定の媒体のデータをセットします。pred[X.columns[i]] = MMM.predict(X_) - baseで各媒体の貢献度を計算します。
- 予測値の補正:
- 実際の売上
yと基本予測pred.yとの比率を計算して補正係数を得ます。 pred_adj = pred.mul(correction_factor, axis=0): この補正係数を用いて、予測値を調整します。
- 実際の売上
- 貢献度の抽出:
contribution = pred_adj.drop(columns=['y']): 補正後の予測値から目的変数yを除外し、各媒体の貢献度のみを保持します。
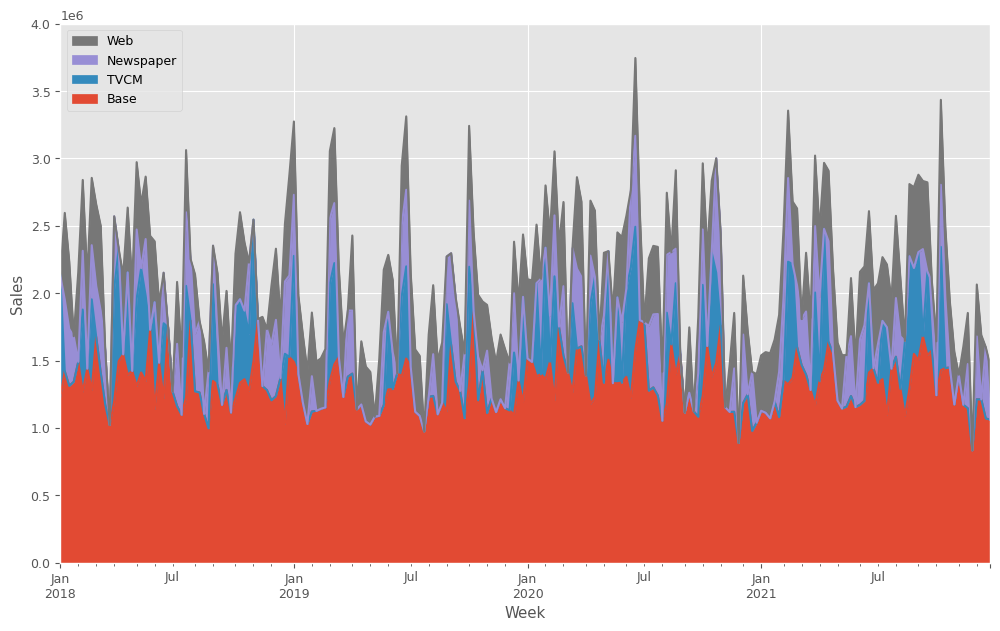
- グラフ化:
contribution.plot.area(...): 各媒体の貢献度をエリアグラフとしてプロットします。xlabelとylabelで軸ラベルを設定します。- 凡例の順序を逆にしてグラフに追加し、y軸の範囲を設定します。
plt.show()でグラフを表示します。
以下、実行結果です。
Base TVCM Newspaper Web Week 2018-01-07 1.228202e+06 903797.818513 0.000000 0.000000 2018-01-14 1.421614e+06 0.000000 531660.030809 642826.237428 2018-01-21 1.312771e+06 0.000000 421836.353351 501592.656646 2018-01-28 1.342945e+06 0.000000 337955.293145 0.000000 2018-02-04 1.490899e+06 0.000000 0.000000 664500.695310 ... ... ... ... ... 2021-11-28 8.339000e+05 0.000000 0.000000 0.000000 2021-12-05 1.213136e+06 0.000000 466142.340592 385422.124234 2021-12-12 1.212401e+06 0.000000 0.000000 477098.500910 2021-12-19 1.070570e+06 0.000000 529030.424496 0.000000 2021-12-26 1.061558e+06 0.000000 0.000000 399541.664901 [208 rows x 4 columns]
メディアの貢献度構成比を計算します。
以下、コードです。
# メディア別の貢献度の合計と構成比の計算と表示
contribution_sum = contribution.sum(axis=0)
contribution_percentage = contribution_sum / contribution_sum.sum()
# 結果を1つのDataFrameにまとめる
contribution_results = pd.DataFrame({
'売上貢献度(円)': contribution_sum,
'売上貢献度(構成比)': contribution_percentage
})
# 結果の出力
print(contribution_results, '\n')
# グラフ化
contribution_sum.plot.pie()
plt.show()
- 貢献度の合計と構成比の計算:
contribution_sum = contribution.sum(axis=0):contributionデータフレームの各列(メディア)の合計値を計算します。- これは各メディアの総貢献度を示します。
contribution_percentage = contribution_sum / contribution_sum.sum():- 各メディアの貢献度の合計に対する構成比を計算します。
- これは、全体に占める各メディアの割合を示しています。
- 結果をDataFrameにまとめる:
contribution_results = pd.DataFrame(...): 貢献度の合計値と構成比を含む新しいDataFrameを作成します。- ここで、売上貢献度(円)と売上貢献度(構成比)の二つの列を持ちます。
- 結果の出力:
print(contribution_results, '\n'): 計算した結果を出力します。
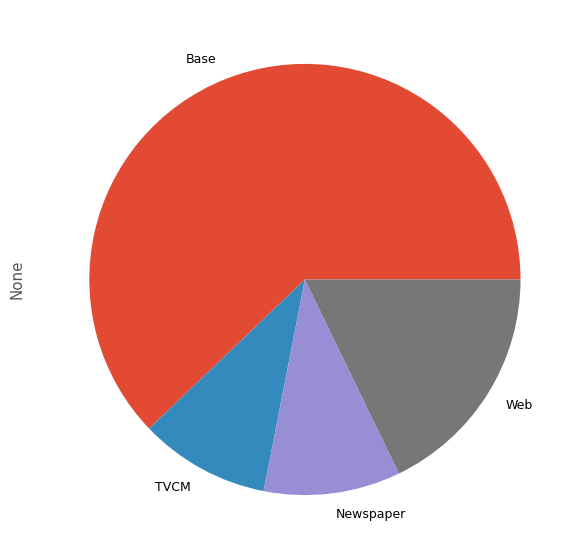
- グラフ化:
contribution_sum.plot.pie(): 各メディアの売上貢献度の合計をパイチャートで表示します。- これにより、各メディアが全体の売上にどれだけ寄与しているかが一目で分かります。
plt.show(): パイチャートを表示します。
以下、実行結果です。
売上貢献度(円) 売上貢献度(構成比) Base 2.725539e+08 0.621480 TVCM 4.290053e+07 0.097822 Newspaper 4.496719e+07 0.102535 Web 7.813451e+07 0.178163
各メディアのマーケティングROIを計算します。
以下、コードです。
#
# マーケティングROIの算定
#
# 各媒体のコストの合計
cost_sum = X.sum(axis=0)
# 各媒体のROIの計算
ROI = (contribution[X.columns].sum(axis=0) - cost_sum)/cost_sum
print('ROI:')
print(ROI)
# グラフ化
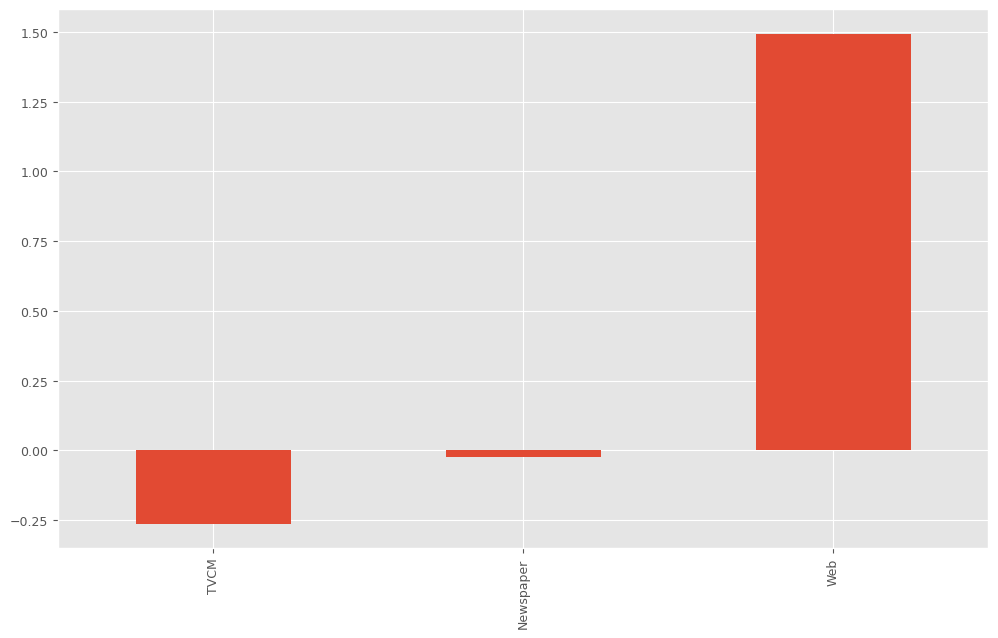
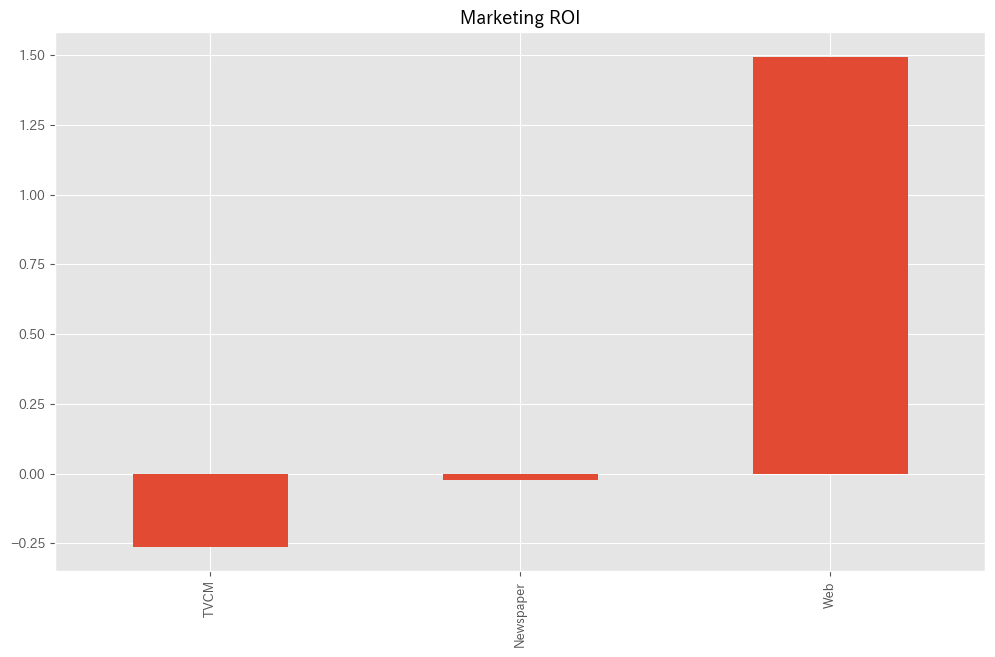
ROI.plot.bar()
- 各媒体のコストの合計計算:
cost_sum = X.sum(axis=0):Xデータフレーム(おそらく各媒体の広告費用を含む)の各列の合計を計算します。- これは、各媒体にかかった総コストを表します。
- 各媒体のROIの計算:
ROI = (contribution[X.columns].sum(axis=0) - cost_sum)/cost_sum: ここでは、先に計算したcontributionデータフレームから基準(’Base’)を除外し、各媒体の貢献度の合計からコストを差し引き、それをコストで割ることで各媒体のROIを計算しています。- ROIは、投資に対するリターンの割合を示し、(リターン – コスト) / コストで計算されます。
- ROIの表示:
print('ROI:')とprint(ROI): 計算したROIの値を表示します。
- ROIのグラフ化:
ROI.plot.bar(): 各媒体のROIを棒グラフで表示します。- これにより、どの媒体が最も高い収益率を提供しているかが一目で分かります。
以下、実行結果です。
ROI: TVCM -0.262212 Newspaper -0.022159 Web 1.493975 dtype: float64
処理を関数化する
先ほど、MMM構築の流れをステップByステップで説明しました。
以降の線形系のモデルでも同様の処理をするため、ここで先ほどの処理を関数化していきます。
関数化するとき、利用する推定器を変えられるように引数にするとかします。
構築する関数
今から構築する関数は以下です。
- MMM構築
train_and_evaluate_model:MMMの構築plot_actual_vs_predicted:構築したMMMの予測値の時系列推移
- 後処理(結果の出力)
calculate_and_plot_contribution:売上貢献度の算出(時系列推移)summarize_and_plot_contribution:売上貢献度構成比の算出calculate_marketing_roi:マーケティングROIの算出
各関数を作った後、各関数の挙動を確認するため、先ほどと同様に線形回帰モデルでMMMを構築してみます。
準備(モジュールとデータの読み込み)
先ず、モジュールを読み込みます。
以下、コードです。
import numpy as np
import pandas as pd
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
from sklearn.metrics import mean_absolute_error
from sklearn.metrics import mean_absolute_percentage_error
from sklearn.metrics import r2_score
import warnings
warnings.simplefilter('ignore')
import matplotlib.pyplot as plt
plt.style.use('ggplot') #グラフスタイル
plt.rcParams['figure.figsize'] = [12, 7] #グラフサイズ
plt.rcParams['font.size'] = 9 #フォントサイズ
次に、データセットを読み込みます。
以下、コードです。
# データセット読み込み
dataset = 'https://www.salesanalytics.co.jp/4zdt'
df = pd.read_csv(
dataset,
parse_dates=['Week'],
index_col='Week',
)
# 説明変数Xと目的変数yに分解
X = df.drop(columns=['Sales'])
y = df['Sales']
これで準場は終了です。以後、関数を作っていきます。
MMM構築用の関数
MMMを構築するための関数を作ります。
以下、コードです。
# MMM構築
def train_and_evaluate_model(model, X, y):
"""
モデルを学習し、予測と評価を行う関数
:param model: 学習するモデルのインスタンス
:param X: 特徴量のデータフレーム
:param y: ターゲット変数のデータフレーム
:return: 学習済みモデルmodel、予測値pred
"""
# モデルの学習
model.fit(X, y)
# 予測
pred = pd.DataFrame(
model.predict(X),
index=X.index,
columns=['y'],
)
# 精度指標の計算
rmse = np.sqrt(mean_squared_error(y, pred))
mae = mean_absolute_error(y, pred)
mape = mean_absolute_percentage_error(y, pred)
r2 = r2_score(y, pred)
# 精度指標の出力
print('RMSE:', rmse)
print('MAE:', mae)
print('MAPE:', mape)
print('R2:', r2)
return model,pred
このコードは、MMMを構築し、学習し、評価するための関数を定義しています。この関数の中でモデルの学習、予測、および評価の各ステップを実行します。
- 関数の定義:
def train_and_evaluate_model(model, X, y): この関数は、機械学習モデル(model)、特徴量(X)、および目的変数(y)をパラメータとして受け取ります。
- モデルの学習:
model.fit(X, y): 与えられた特徴量Xと目的変数yを使用して、モデルを学習させます。
- 予測の生成:
pred = pd.DataFrame(...): 学習済みモデルを使用してXに基づいた予測を行い、その結果をPandasのデータフレームとして格納します。
- 精度指標の計算:
- 予測値
predと実際の値yを比較して、以下の精度指標を計算します:- RMSE(Root Mean Squared Error)
- MAE(Mean Absolute Error)
- MAPE(Mean Absolute Percentage Error)
- R²(Coefficient of Determination)
- 予測値
- 精度指標の出力:
printステートメントを使用して、計算された精度指標の値を出力します。
- 戻り値:
return model, pred: 関数は学習済みのモデルmodelと予測値predのデータフレームを返します。
この関数は、モデルの構築、学習、予測、および評価を一連のプロセスとして包括的に行うことができるため、マーケティングデータ分析や機械学習タスクにおいて非常に便利です。特にマーケティングの効果を定量化し、異なるメディアや戦略が売上に与える影響を分析する際に有用です。
この関数train_and_evaluate_modelを使い、線形回帰モデルのMMMを構築します。
以下、コードです。
# MMM構築 model = LinearRegression() trained_model,pred = train_and_evaluate_model(model, X, y)
以下、実行結果です。
RMSE: 284667.75543375366 MAE: 237679.0368036913 MAPE: 0.12129533117151893 R2: 0.7400400171566187
MMMの予測値(predicted)と実測値(actual)の推移をプロットする関数を作ります。
以下、コードです。
# 実測値と予測値の時系列推移
def plot_actual_vs_predicted(index, actual_values, predicted_values, ylim):
"""
実際の値と予測値を比較するグラフを描画する関数。
:param index: データのインデックス
:param actual_values: 実際の値の配列
:param predicted_values: 予測値の配列
:param ylim: y軸の表示範囲
"""
fig, ax = plt.subplots()
ax.plot(index, actual_values, label="actual")
ax.plot(index, predicted_values, label="predicted", linestyle="dotted", lw=2)
ax.set_ylim(ylim)
plt.title('Time series of actual and predicted values')
plt.legend()
plt.show()
このコードは、実測値と予測値の時系列推移を比較するグラフを描画するための関数plot_actual_vs_predictedを定義しています。この関数は、時系列データの実測値と予測値を同じグラフ上で視覚的に比較することを目的としています。
- 関数の定義:
def plot_actual_vs_predicted(index, actual_values, predicted_values, ylim): この関数は、データのインデックス(index)、実際の値(actual_values)、予測値(predicted_values)、およびy軸の表示範囲(ylim)を引数として受け取ります。
- グラフの準備:
fig, ax = plt.subplots(): Matplotlibを使用して、グラフを描画するための図(fig)と座標軸(ax)を作成します。
- 実測値と予測値のプロット:
ax.plot(index, actual_values, label="actual"): 実測値を線グラフでプロットします。label="actual"は、この線が実測値を表していることを示すラベルです。ax.plot(index, predicted_values, label="predicted", linestyle="dotted", lw=2): 予測値も線グラフでプロットしますが、点線スタイル(linestyle="dotted")と線の太さ(lw=2)を指定して、実測値と視覚的に区別します。
- グラフの設定:
ax.set_ylim(ylim): y軸の表示範囲をylim引数で指定された範囲に設定します。
- タイトルと凡例の設定、グラフの表示:
plt.title('Time series of actual and predicted values'): グラフにタイトルを設定します。plt.legend(): 凡例を表示します。plt.show(): 最終的にグラフを画面に表示します。
この関数は、マーケティング分析、金融分析、気象予測など、様々な時系列データを扱う分野での予測モデルのパフォーマンス評価に役立ちます。実測値と予測値を直接比較することで、モデルの精度と時系列データにおけるその振る舞いをよりよく理解することができます。
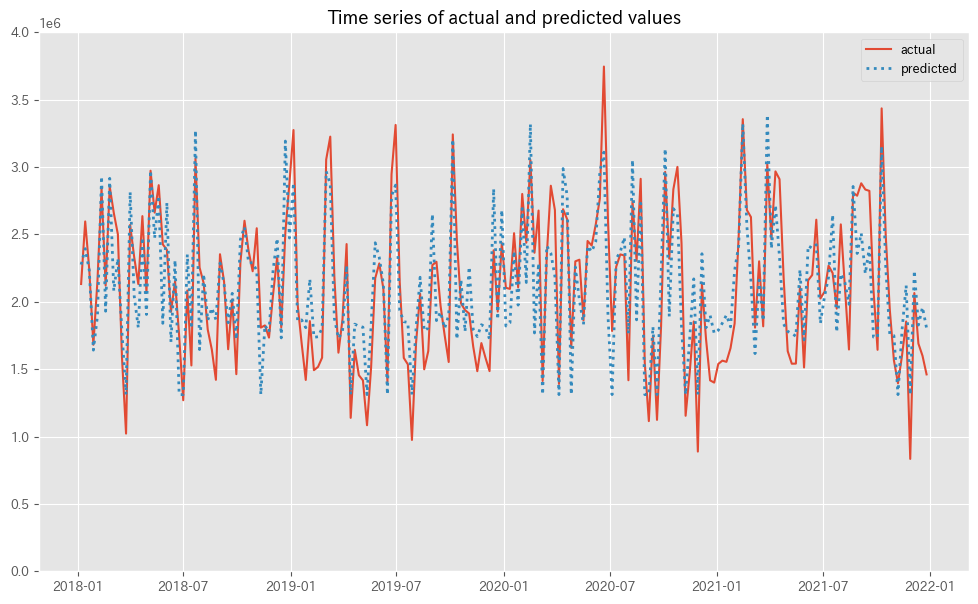
関数plot_actual_vs_predictedを使い、関数train_and_evaluate_modelで構築したMMMの予測値と実測値をプロットします。
以下、コードです。
# 実測値と予測値の時系列推移 plot_actual_vs_predicted(y.index, y.values, pred.y.values, (0, 4e6))
以下、実行結果です。
後処理(結果の出力)用の関数
予測値を元に、貢献度を算定する関数を作ります。
以下、コードです。
# 貢献度の算出
def calculate_and_plot_contribution(y, X, model, ylim):
"""
各媒体の売上貢献度を算定し、結果をプロットする関数。
:param y: ターゲット変数
:param X: 特徴量のデータフレーム
:param model: 学習済みモデル
:param ylim: y軸の表示範囲
:return: 各媒体の貢献度
"""
# yの予測
pred = pd.DataFrame(
model.predict(X),
index=X.index,
columns=['y'],
)
# 値がすべて0の説明変数
X_ = X.copy()
X_.iloc[:, :] = 0
# Baseの予測
base = model.predict(X_)
pred['Base'] = base
# 各媒体の予測
for i in range(len(X.columns)):
X_.iloc[:, :] = 0
X_.iloc[:, i] = X.iloc[:, i]
pred[X.columns[i]] = model.predict(X_) - base
# 予測値の補正
correction_factor = y.div(pred.y, axis=0)
pred_adj = pred.mul(correction_factor, axis=0)
contribution = pred_adj.drop(columns=['y'])
# 結果の出力
print(contribution, '\n')
# エリアプロット
ax = contribution.plot.area()
handles, labels = ax.get_legend_handles_labels()
ax.legend(reversed(handles), reversed(labels))
ax.set_ylim(ylim)
plt.title('Contributions over time')
plt.show()
return contribution
このコードは、マーケティングの各媒体が売上に与える貢献度を算定し、その結果をエリアプロットで視覚化するための関数calculate_and_plot_contributionを定義しています。
- 関数の定義:
def calculate_and_plot_contribution(y, X, model, ylim): この関数は、ターゲット変数y、特徴量のデータフレームX、学習済みモデルmodel、およびy軸の表示範囲ylimを引数として受け取ります。
- 予測の生成:
pred = pd.DataFrame(...): 学習済みモデルを使用してXに基づいた予測を行い、その結果をPandasのデータフレームとして格納します。
- 基準値(Base)の予測:
X_ = X.copy():Xのコピーを作成し、すべての列を0に設定して基準値のシナリオを作ります。base = model.predict(X_): すべての媒体の効果を除外した基準状態での売上予測を行います。pred['Base'] = base: この基準予測をpredデータフレームに追加します。
- 各媒体の貢献度計算:
- 各媒体の影響を一つずつ追加しながら予測を行い、基準値からの差分を計算して各媒体の貢献度を求めます。
- 予測値の補正:
- 実際の売上
yと基本予測pred.yとの比率を計算して補正係数を得ます。 pred_adj = pred.mul(correction_factor, axis=0): この補正係数を用いて、予測値を調整します。
- 実際の売上
- エリアプロットでの視覚化:
contribution.plot.area(): 補正後の予測値から目的変数yを除外し、各媒体の貢献度をエリアプロットで表示します。- 凡例の順序を逆にしてグラフに追加し、y軸の範囲を設定し、タイトルを付けてグラフを表示します。
- 戻り値:
return contribution: 計算した各媒体の貢献度を返します。
この関数は、マーケティング活動の効果をより深く理解するために役立ちます。各媒体が時間の経過とともに売上にどのように影響を与えているかを視覚化することで、効果的なマーケティング戦略の策定に貢献します。
関数calculate_and_plot_contributionを使い、貢献度を算定します。
以下、コードです。
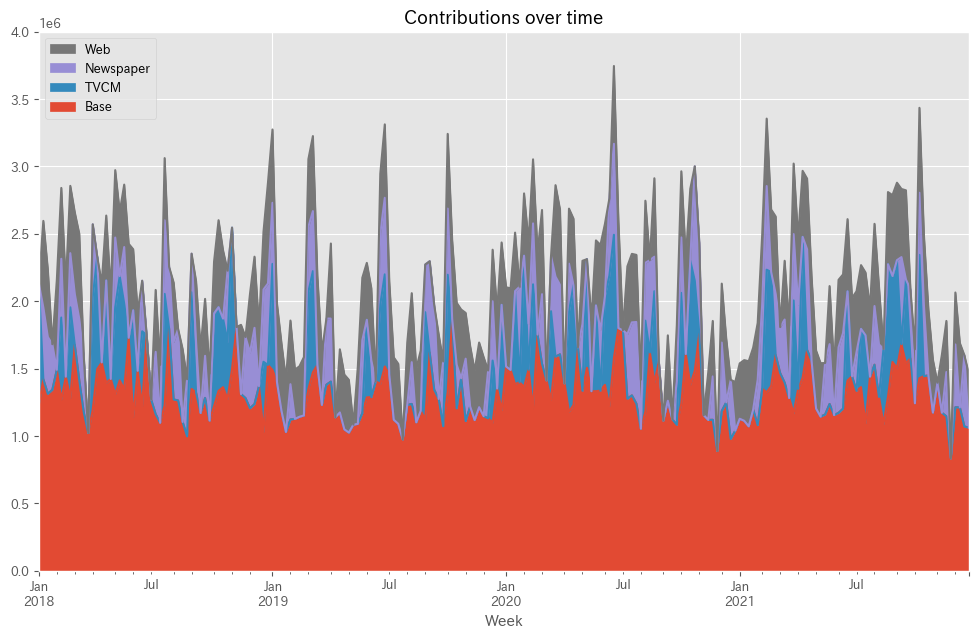
# 貢献度の算出 contribution = calculate_and_plot_contribution(y, X, trained_model,(0, 4e6))
以下、実行結果です。
Base TVCM Newspaper Web Week 2018-01-07 1.228202e+06 903797.818513 0.000000 0.000000 2018-01-14 1.421614e+06 0.000000 531660.030809 642826.237428 2018-01-21 1.312771e+06 0.000000 421836.353351 501592.656646 2018-01-28 1.342945e+06 0.000000 337955.293145 0.000000 2018-02-04 1.490899e+06 0.000000 0.000000 664500.695310 ... ... ... ... ... 2021-11-28 8.339000e+05 0.000000 0.000000 0.000000 2021-12-05 1.213136e+06 0.000000 466142.340592 385422.124234 2021-12-12 1.212401e+06 0.000000 0.000000 477098.500910 2021-12-19 1.070570e+06 0.000000 529030.424496 0.000000 2021-12-26 1.061558e+06 0.000000 0.000000 399541.664901 [208 rows x 4 columns]
メディアの貢献度構成比を計算する関数を作ります。
以下、コードです。
# 貢献度構成比の算出
def summarize_and_plot_contribution(contribution):
"""
媒体別の売上貢献度の合計と構成比を計算し、結果を表示する関数
:param contribution: 各媒体の貢献度を含むデータフレーム
:return: 売上貢献度の合計と構成比を含むデータフレーム
"""
# 各媒体の貢献度の合計
contribution_sum = contribution.sum(axis=0)
# 各媒体の貢献度の構成比
contribution_percentage = contribution_sum / contribution_sum.sum()
# 結果を1つのDataFrameにまとめる
contribution_results = pd.DataFrame({
'contribution': contribution_sum,
'ratio': contribution_percentage
})
# 結果の出力
print(contribution_results, '\n')
# グラフ化
contribution_sum.plot.pie()
plt.title('Contribution Composition Ratio')
plt.show()
return contribution_results
このコードは、マーケティングの各媒体が売上に与える貢献度の合計と構成比を計算し、それらを表示および視覚化するための関数summarize_and_plot_contributionを定義しています。
- 関数の定義:
def summarize_and_plot_contribution(contribution): この関数は、各媒体の貢献度を含むデータフレームcontributionを引数として受け取ります。
- 貢献度の合計計算:
contribution_sum = contribution.sum(axis=0): 各媒体の貢献度を合計します。sum(axis=0)は列方向の合計を意味します。
- 貢献度の構成比計算:
contribution_percentage = contribution_sum / contribution_sum.sum(): 各媒体の貢献度の合計に対する構成比を計算します。- これは、全体に占める各媒体の割合を示します。
- 結果のデータフレーム作成:
contribution_results = pd.DataFrame(...): 貢献度の合計と構成比を含む新しいデータフレームを作成します。
- 結果の出力:
print(contribution_results, '\n'): 計算した貢献度の合計と構成比の結果を出力します。
- 結果のグラフ化:
contribution_sum.plot.pie(): 各媒体の貢献度の合計をパイチャートで表示します。これにより、各媒体が全体の売上にどれだけ寄与しているかを視覚的に理解できます。plt.title('Contribution Composition Ratio'): グラフにタイトルを設定します。plt.show(): パイチャートを表示します。
- 戻り値:
return contribution_results: 計算した貢献度の合計と構成比を含むデータフレームを返します。
この関数は、マーケティング効果の分析や戦略立案において重要です。各媒体の貢献度を量的にも視覚的にも理解することができ、予算配分や将来のマーケティング活動の調整に役立ちます。
メディアの貢献度構成比を計算します。
以下、コードです。
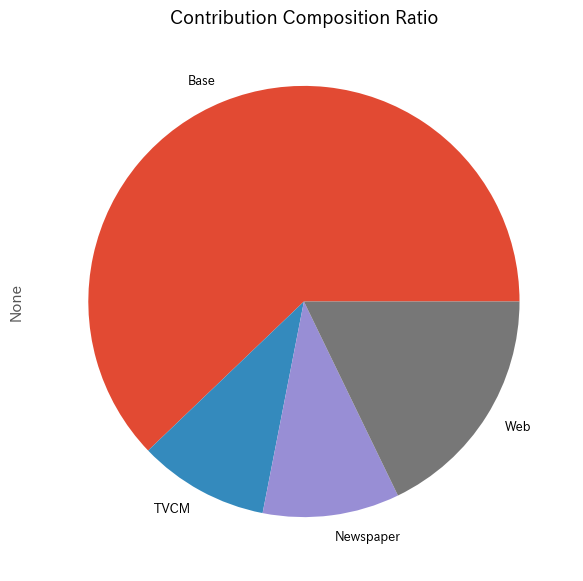
# 貢献度構成比の算出 contribution_results = summarize_and_plot_contribution(contribution)
以下、実行結果です。
contribution ratio Base 2.725539e+08 0.621480 TVCM 4.290053e+07 0.097822 Newspaper 4.496719e+07 0.102535 Web 7.813451e+07 0.178163
各メディアのマーケティングROIを計算する関数を作ります。
以下、コードです。
# マーケティングROIの算出
def calculate_marketing_roi(X, contribution):
"""
各媒体のマーケティングROIを算定する関数。
:param X: 各媒体のコストを含むデータフレーム
:param contribution: 各媒体の売上貢献度を含むデータフレーム
:return: 各媒体のROIを含むデータフレーム
"""
# 各媒体のコストの合計
cost_sum = X.sum(axis=0)
# 各媒体のROIの計算
ROI = (contribution[X.columns].sum(axis=0) - cost_sum)/cost_sum
# 結果の出力
print(ROI, '\n')
# グラフ
ROI.plot.bar()
plt.title('Marketing ROI')
plt.show()
return ROI
各メディアのマーケティングROIを計算します。
以下、コードです。
# マーケティングROIの算出 ROI = calculate_marketing_roi(X, contribution)
以下、実行結果です。
TVCM -0.262212 Newspaper -0.022159 Web 1.493975 dtype: float64
関数をpyファイルに保存し流用
今、以下の関数を定義しました。
- MMM構築
train_and_evaluate_model:MMMの構築plot_actual_vs_predicted:構築したMMMの予測値の時系列推移
- 後処理(結果の出力)
calculate_and_plot_contribution:売上貢献度の算出(時系列推移)summarize_and_plot_contribution:売上貢献度構成比の算出calculate_marketing_roi:マーケティングROIの算出
これらの関数を使い、他の線形系のモデルでMMMを構築していきます。
そのために、これらの関数をまとめたPythonファイル(mmm_functions.py)を使い、他の線形系のモデルでMMMを構築していくとき、このPythonファイルに記載されている関数を使います。
以下からダウンロードできます。
mmm_functions.py ※zipファイルを解凍してお使いください
https://www.salesanalytics.co.jp/oi17
以下、mmm_functions.pyの中に記載されているコードです。
import numpy as np
import pandas as pd
from sklearn.metrics import mean_squared_error
from sklearn.metrics import mean_absolute_error
from sklearn.metrics import mean_absolute_percentage_error
from sklearn.metrics import r2_score
import warnings
warnings.simplefilter('ignore')
import matplotlib.pyplot as plt
plt.style.use('ggplot') #グラフスタイル
plt.rcParams['figure.figsize'] = [12, 7] #グラフサイズ
plt.rcParams['font.size'] = 9 #フォントサイズ
# MMM構築
def train_and_evaluate_model(model, X, y):
"""
モデルを学習し、予測と評価を行う関数。
:param model: 学習するモデルのインスタンス
:param X: 特徴量のデータフレーム
:param y: ターゲット変数のデータフレーム
:return: 学習済みモデルmodel、予測値pred
"""
# モデルの学習
model.fit(X, y)
# 予測
pred = pd.DataFrame(
model.predict(X),
index=X.index,
columns=['y'],
)
# 精度指標の計算
rmse = np.sqrt(mean_squared_error(y, pred))
mae = mean_absolute_error(y, pred)
mape = mean_absolute_percentage_error(y, pred)
r2 = r2_score(y, pred)
# 精度指標の出力
print('RMSE:', rmse)
print('MAE:', mae)
print('MAPE:', mape)
print('R2:', r2)
return model,pred
# 実測値と予測値の時系列推移
def plot_actual_vs_predicted(index, actual_values, predicted_values, ylim):
"""
実際の値と予測値を比較するグラフを描画する関数。
:param index: データのインデックス
:param actual_values: 実際の値の配列
:param predicted_values: 予測値の配列
:param ylim: y軸の表示範囲
"""
fig, ax = plt.subplots()
ax.plot(index, actual_values, label="actual")
ax.plot(index, predicted_values, label="predicted", linestyle="dotted", lw=2)
ax.set_ylim(ylim)
plt.title('Time series of actual and predicted values')
plt.legend()
plt.show()
# 貢献度の算出
def calculate_and_plot_contribution(y, X, model, ylim):
"""
各媒体の売上貢献度を算定し、結果をプロットする関数。
:param y: ターゲット変数
:param X: 特徴量のデータフレーム
:param model: 学習済みモデル
:param ylim: y軸の表示範囲
:return: 各媒体の貢献度
"""
# yの予測
pred = pd.DataFrame(
model.predict(X),
index=X.index,
columns=['y'],
)
# 値がすべて0の説明変数
X_ = X.copy()
X_.iloc[:, :] = 0
# Baseの予測
base = model.predict(X_)
pred['Base'] = base
# 各媒体の予測
for i in range(len(X.columns)):
X_.iloc[:, :] = 0
X_.iloc[:, i] = X.iloc[:, i]
pred[X.columns[i]] = model.predict(X_) - base
# 予測値の補正
correction_factor = y.div(pred.y, axis=0)
pred_adj = pred.mul(correction_factor, axis=0)
contribution = pred_adj.drop(columns=['y'])
# 結果の出力
print(contribution, '\n')
# エリアプロット
ax = contribution.plot.area()
handles, labels = ax.get_legend_handles_labels()
ax.legend(reversed(handles), reversed(labels))
ax.set_ylim(ylim)
plt.title('Contributions over time')
plt.show()
return contribution
# 貢献度構成比の算出
def summarize_and_plot_contribution(contribution):
"""
媒体別の売上貢献度の合計と構成比を計算し、結果を表示する関数。
:param contribution: 各媒体の貢献度を含むデータフレーム
:return: 売上貢献度の合計と構成比を含むデータフレーム
"""
# 各媒体の貢献度の合計
contribution_sum = contribution.sum(axis=0)
# 各媒体の貢献度の構成比
contribution_percentage = contribution_sum / contribution_sum.sum()
# 結果を1つのDataFrameにまとめる
contribution_results = pd.DataFrame({
'contribution': contribution_sum,
'ratio': contribution_percentage
})
# 結果の出力
print(contribution_results, '\n')
# グラフ化
contribution_sum.plot.pie()
plt.title('Contribution Composition Ratio')
plt.show()
return contribution_results
# マーケティングROIの算出
def calculate_marketing_roi(X, contribution):
"""
各媒体のマーケティングROIを算定する関数。
:param X: 各媒体のコストを含むデータフレーム
:param contribution: 各媒体の売上貢献度を含むデータフレーム
:return: 各媒体のROIを含むデータフレーム
"""
# 各媒体のコストの合計
cost_sum = X.sum(axis=0)
# 各媒体のROIの計算
ROI = (contribution[X.columns].sum(axis=0) - cost_sum)/cost_sum
# 結果の出力
print(ROI, '\n')
# グラフ
ROI.plot.bar()
plt.title('Marketing ROI')
plt.show()
return ROI
mmm_functions.pyを利用するときは、実行するPythonファイルやNotebookと同じフォルダに入れておいてください。
以下のコードで呼び出せます。
from mmm_functions import *
上手くいかないときは、mmm_functions.pyをメモ帳などで開き内容をコピーし、実行するPythonファイルやNotebookにコードを張り付け、Pythonで関数を作ってからMMM構築などを行ってください。
発展的話題①
– 様々な線形回帰系モデルで構築するMMM
リッジ回帰でMMM
scikit-learn(sklearn)ライブラリーのRidge(L2正則化を加えた線形回帰)でMMMを構築します。
リッジ回帰にはハイパーパラメータがありますので、それをOptunaでチューニングします。
今回は以下の2種類のモデルを作ります。
- ハイパーパラメータをデフォルトのまま(Optunaによるハイパラ調整なし)MMM構築
- Optunaによるハイパーパラメータ調整しMMM構築
リッジ回帰とは?
scikit-learn(sklearn)ライブラリーにおける Ridge は、L2正則化を加えた線形回帰モデルです。この手法は、特に多重共線性(独立変数間の高い相関)が存在する場合に有用です。
- L2正則化:
Ridge回帰は、線形回帰モデルにL2正則化項を加えることで、モデルの係数が大きくなりすぎることを防ぎます。この正則化項は、係数の二乗和に基づいており、モデルがデータに過剰に適合することを防ぎます(過学習を防ぐ)。 - 係数の縮小: 正則化により、回帰係数はデータに完全に適合するよりも、より小さな値に縮小されます。これにより、モデルの予測精度が向上し、一般化能力が高まります。
- 多重共線性の緩和:
Ridge回帰は、特徴間の相関が高い場合に生じる多重共線性の問題を軽減します。これにより、モデルの安定性と予測精度が向上します。 - ハイパーパラメータ α: 正則化の強さはハイパーパラメータ α によって制御されます。α が大きいほど強い正則化が適用され、係数はより小さくなります。逆に、α が小さいと、
Ridge回帰は通常の線形回帰に近づきます。デフォルトは 1 です。
Ridge 回帰は、販売予測、顧客行動分析、在庫管理、リスク評価など、様々なビジネスアプリケーションで利用されます。特に、多くの特徴量が相関している複雑なデータセットを扱う場合、より堅牢なモデルを構築するために使用されます。
準備(モジュールとデータの読み込み)
必要なモジュールを読み込みます。
以下、コードです。
import numpy as np import pandas as pd import optuna from sklearn.model_selection import TimeSeriesSplit from sklearn.linear_model import Ridge from mmm_functions import *
データセットを読み込みます。
以下、コードです。
# データセット読み込み
dataset = 'https://www.salesanalytics.co.jp/4zdt'
df = pd.read_csv(
dataset,
parse_dates=['Week'],
index_col='Week',
)
# 説明変数Xと目的変数yに分解
X = df.drop(columns=['Sales'])
y = df['Sales']
ハイパーパラメータをデフォルトのままMMM構築
リッジ回帰モデルでMMMを構築します。
以下、コードです。
# MMMの構築 model = Ridge(**best_params) trained_model,pred = train_and_evaluate_model(model, X, y)
以下、実行結果です。
RMSE: 284667.75543375366 MAE: 237679.03680369718 MAPE: 0.12129533117155332 R2: 0.7400400171566187
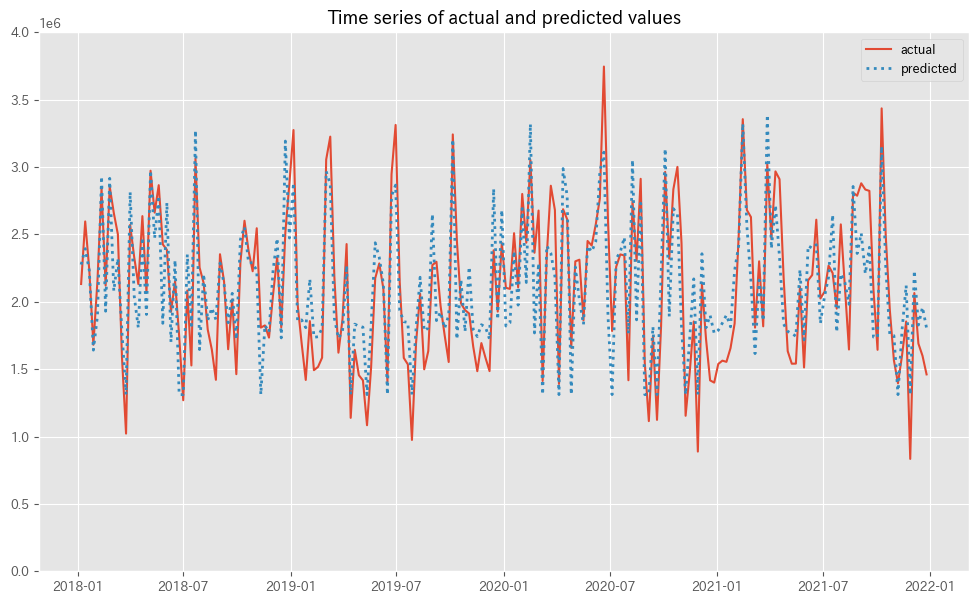
MMMの予測値(predicted)と実測値(actual)の推移をプロットします。
以下、コードです。
# 実測値と予測値の時系列推移 plot_actual_vs_predicted(y.index, y.values, pred.y.values, (0, 4e6))
以下、実行結果です。
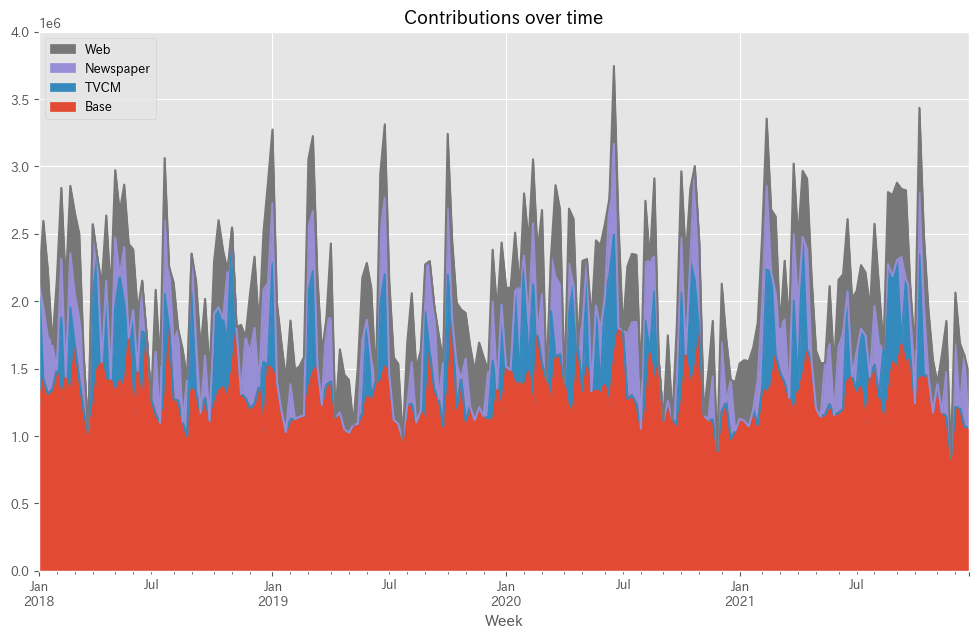
予測値を元に、貢献度を算定します。
以下、コードです。
# 貢献度の算出 contribution = calculate_and_plot_contribution(y, X, trained_model, (0, 4e6))
以下、実行結果です。
Base TVCM Newspaper Web Week 2018-01-07 1.228202e+06 903797.818512 0.000000 0.000000 2018-01-14 1.421614e+06 0.000000 531660.030809 642826.237425 2018-01-21 1.312771e+06 0.000000 421836.353350 501592.656643 2018-01-28 1.342945e+06 0.000000 337955.293144 0.000000 2018-02-04 1.490899e+06 0.000000 0.000000 664500.695306 ... ... ... ... ... 2021-11-28 8.339000e+05 0.000000 0.000000 0.000000 2021-12-05 1.213136e+06 0.000000 466142.340591 385422.124231 2021-12-12 1.212401e+06 0.000000 0.000000 477098.500907 2021-12-19 1.070570e+06 0.000000 529030.424494 0.000000 2021-12-26 1.061558e+06 0.000000 0.000000 399541.664899 [208 rows x 4 columns]
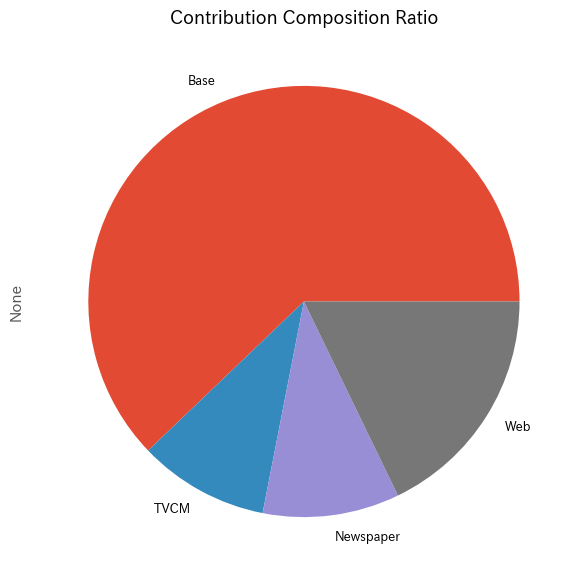
メディアの貢献度構成比を計算します。
以下、コードです。
# 貢献度構成比の算出 contribution_results = summarize_and_plot_contribution(contribution)
以下、実行結果です。
contribution ratio Base 2.725539e+08 0.621480 TVCM 4.290053e+07 0.097822 Newspaper 4.496719e+07 0.102535 Web 7.813451e+07 0.178163
各メディアのマーケティングROIを計算します。
以下、コードです。
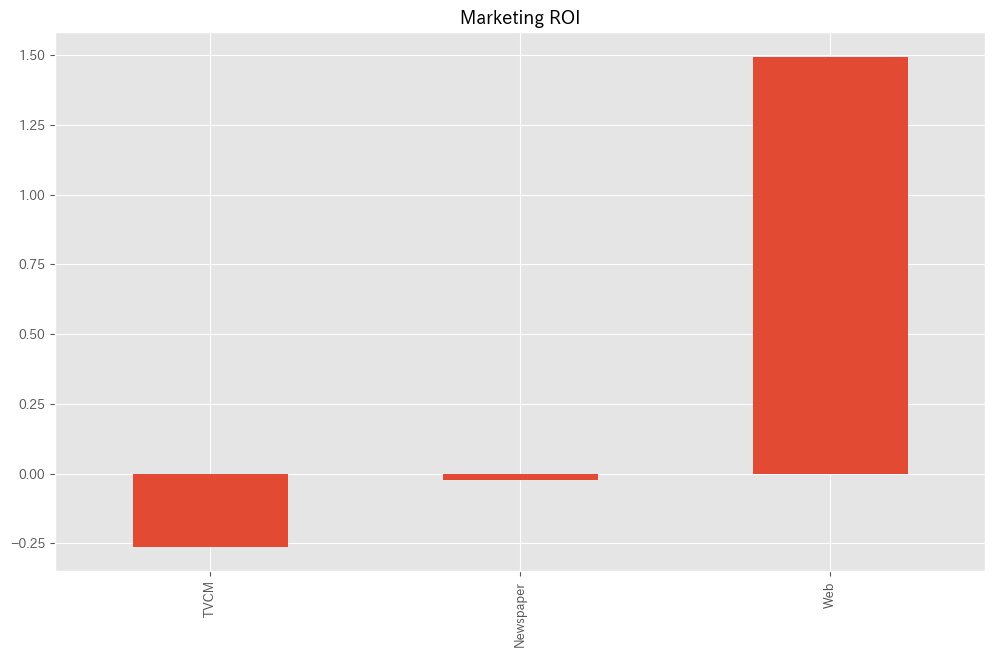
# マーケティングROIの算出 ROI = calculate_marketing_roi(X, contribution)
以下、実行結果です。
TVCM -0.262212 Newspaper -0.022159 Web 1.493975 dtype: float64
Optunaによるハイパーパラメータ調整しMMM構築
Optunaの目的関数を定義します。
以下、コードです。
# Optunaの目的関数の設定
def objective(trial):
# Optunaの試行で使用するalpha値を提案
alpha = trial.suggest_float('alpha', 1e-3, 10.0, log=True)
# Ridgeモデルのインスタンス化
model = Ridge(alpha=alpha)
# TimeSeriesSplitによるクロスバリデーション
tscv = TimeSeriesSplit(n_splits=5)
scores = cross_val_score(model, X, y, cv=tscv, scoring='neg_mean_squared_error')
rmse = np.mean([np.sqrt(-score) for score in scores])
# 平均RMSEを返す
return rmse
このコードは、Optunaを使用してMMMで利用する時系列データに対するRidge回帰モデルのハイパーパラメータを最適化するための目的関数を定義しています。Optunaはハイパーパラメータの自動チューニングに用いられるライブラリで、目的関数を最小化(または最大化)するハイパーパラメータのセットを探索します。
- 目的関数
objective- この関数は、Optunaの最適化プロセスによって繰り返し呼び出され、異なるハイパーパラメータのセットでモデルの性能を評価します。
- ハイパーパラメータ
alphaの提案trial.suggest_float('alpha', 1e-3, 10.0, log=True): Optunaの試行(trial)オブジェクトを使用して、Ridge回帰モデルの正則化強度を制御するalphaパラメータの値を提案します。- この値は、$10^{-3}$から$10$の範囲で対数スケール(
log=True)で選択されます。対数スケールを使用することで、広範囲にわたる値を効率的に探索できます。
- Ridge回帰モデル
Ridge(alpha=alpha): 提案されたalpha値を使用して、Ridge回帰モデルのインスタンスを作成します。- Ridge回帰は、回帰係数の大きさにペナルティを課すことで、モデルの過学習を抑制する正則化手法です。
- クロスバリデーション
TimeSeriesSplit(n_splits=5): 時系列データのクロスバリデーションに特化したTimeSeriesSplitを使用します。これにより、時系列の順序を保ちながらデータを5つの連続するトレーニングセットとテストセットに分割します。cross_val_score(model, X, y, cv=tscv, scoring='neg_mean_squared_error'): 分割したデータセットに対して、Ridgeモデルのクロスバリデーションを実施し、各分割におけるスコア(負の平均二乗誤差)を計算します。
- 性能指標としてのRMSE
- 負の平均二乗誤差のスコアを平方根して正のRMSE(Root Mean Squared Error、平均二乗誤差の平方根)を計算し、それらの平均値を目的関数の戻り値として返します。RMSEは、予測誤差の大きさを評価する指標であり、この値を最小化することが最適化の目標です。
この目的関数をOptunaのスタディで使用することにより、Ridge回帰モデルのalphaパラメータを最適化し、予測性能を向上させることが目指されます。
目的関数を最適化し、最適なハイパーパラメータを探索します。
以下、コードです。
# Optunaのスタディを作成し、目的関数を最適化
study = optuna.create_study(direction='minimize')
study.optimize(objective, n_trials=1000)
# 最適なハイパーパラメータの表示
best_params = study.best_trial.params
print('Best trial:', best_params)
このコードは、Optunaを使用して特定の目的関数を最適化するためのステップを示しています。ここでの目的は、前述のobjective関数を用いてRidge回帰モデルの最適なハイパーパラメータを見つけることです。
- Optunaスタディの作成:
study = optuna.create_study(direction='minimize'): Optunaのスタディ(最適化プロセス)を作成します。direction='minimize'は、目的関数の値を最小化することが目的であることを指定しています。- これは、前述の
objective関数がRMSE(平均二乗誤差の平方根)を返し、この値を最小化することが望ましいためです。
- 目的関数の最適化:
study.optimize(objective, n_trials=1000): スタディでobjective関数を最適化します。n_trials=1000は、最適化プロセスで試行される総回数を1000回に設定しています。- Optunaはこれらの試行を通じて、最適なハイパーパラメータを見つけ出します。
- 最適なハイパーパラメータの表示:
best_params = study.best_trial.params: 最適化プロセスが完了した後、最適な試行(ハイパーパラメータのセット)を取得します。print('Best trial:', best_params): 最適な試行のパラメータを表示します。これにより、モデルのパフォーマンスを最大化するためのハイパーパラメータの値が明らかになります。
以下、実行結果です。
Best trial: {'alpha': 9.997432010127438}
最適なハイパーパラメータを使いMMMを構築します。
以下、コードです。
# MMMの構築 model = Ridge(**best_params) trained_model,pred = train_and_evaluate_model(model, X, y)
このコードは、以前にOptunaを使用して見つけた最適なハイパーパラメータ(best_params)を用いてRidge回帰モデルを構築し、そのモデルを訓練および評価するプロセスを示しています。
- Ridgeモデルのインスタンス化:
model = Ridge(**best_params): Ridge回帰モデルのインスタンスを作成します。**best_paramsは、Optunaを通じて得られた最適なハイパーパラメータ(正則化項の強さを制御するalpha値)をモデルに渡しています。
- モデルの訓練と評価:
trained_model, pred = train_and_evaluate_model(model, X, y): 以前に定義されたtrain_and_evaluate_model関数を使用して、モデルを訓練し、評価します。- この関数は、訓練データセット(
Xとy)に基づいてモデルを学習させ、予測を行い、パフォーマンス指標(例えばRMSEなど)を計算します。
この手順により、最適化されたハイパーパラメータを持つモデルが構築され、そのモデルのパフォーマンスが評価されます。このプロセスは、特にマーケティングミックスモデリング(MMM)の文脈で、キャンペーンの効果や異なるマーケティングチャネルの寄与を定量的に評価する際に重要です。
以下、実行結果です。
RMSE: 284667.75543375366 MAE: 237679.03680369718 MAPE: 0.12129533117155332 R2: 0.7400400171566187
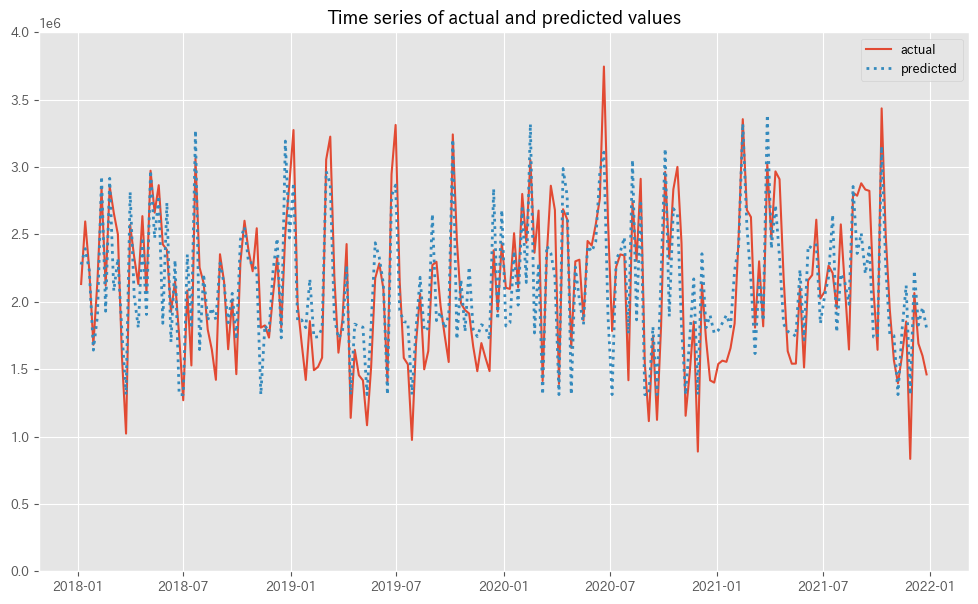
MMMの予測値(predicted)と実測値(actual)の推移をプロットします。
以下、コードです。
# 実測値と予測値の時系列推移 plot_actual_vs_predicted(y.index, y.values, pred.y.values, (0, 4e6))
以下、実行結果です。
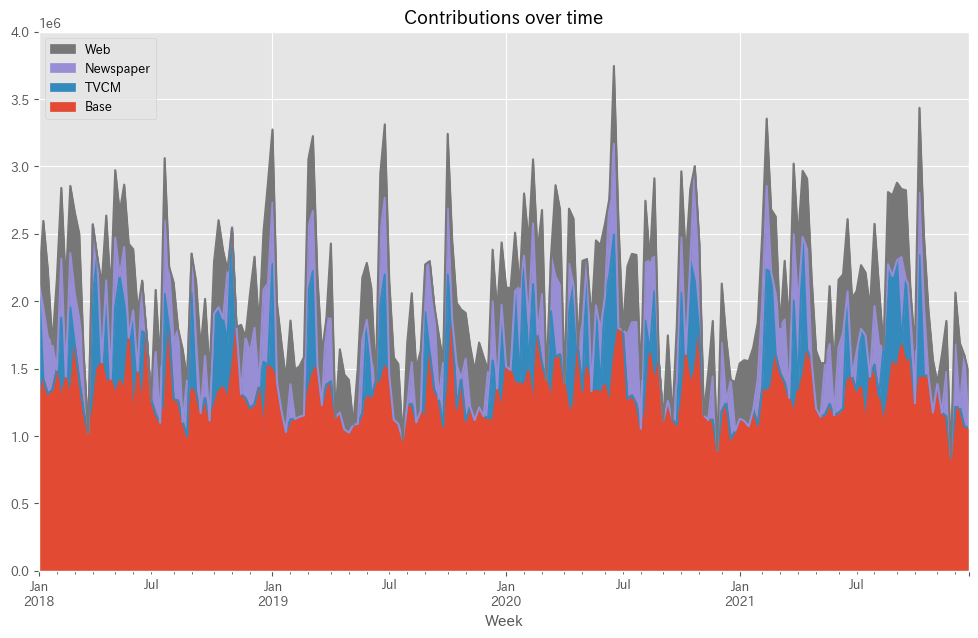
予測値を元に、貢献度を算定します。
以下、コードです。
# 貢献度の算出 contribution = calculate_and_plot_contribution(y, X, trained_model, (0, 4e6))
以下、実行結果です。
Base TVCM Newspaper Web Week 2018-01-07 1.228202e+06 903797.818512 0.000000 0.000000 2018-01-14 1.421614e+06 0.000000 531660.030809 642826.237425 2018-01-21 1.312771e+06 0.000000 421836.353350 501592.656643 2018-01-28 1.342945e+06 0.000000 337955.293144 0.000000 2018-02-04 1.490899e+06 0.000000 0.000000 664500.695306 ... ... ... ... ... 2021-11-28 8.339000e+05 0.000000 0.000000 0.000000 2021-12-05 1.213136e+06 0.000000 466142.340591 385422.124231 2021-12-12 1.212401e+06 0.000000 0.000000 477098.500907 2021-12-19 1.070570e+06 0.000000 529030.424494 0.000000 2021-12-26 1.061558e+06 0.000000 0.000000 399541.664899 [208 rows x 4 columns]
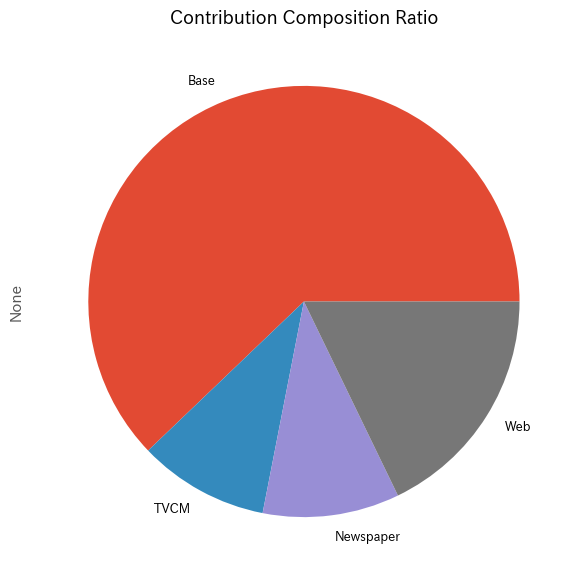
メディアの貢献度構成比を計算します。
以下、コードです。
# 貢献度構成比の算出 contribution_results = summarize_and_plot_contribution(contribution)
以下、実行結果です。
contribution ratio Base 2.725539e+08 0.621480 TVCM 4.290053e+07 0.097822 Newspaper 4.496719e+07 0.102535 Web 7.813451e+07 0.178163
各メディアのマーケティングROIを計算します。
以下、コードです。
# マーケティングROIの算出 ROI = calculate_marketing_roi(X, contribution)
以下、実行結果です。
TVCM -0.262212 Newspaper -0.022159 Web 1.493975 dtype: float64
ベイズリッジ回帰でMMM
scikit-learn(sklearn)ライブラリーのBayesianRidge(ベイズ統計に基づいたリッジ回帰)でMMMを構築します。
ベイズリッジ回帰にはハイパーパラメータがありますので、それをOptunaでチューニングします。
今回は以下の2種類のモデルを作ります。
- ハイパーパラメータをデフォルトのまま(Optunaによるハイパラ調整なし)MMM構築
- Optunaによるハイパーパラメータ調整しMMM構築
ベイズリッジ回帰とは?
scikit-learn(sklearn)ライブラリーの BayesianRidge は、ベイズ統計に基づいたリッジ回帰の形式を採用したモデルです。従来のリッジ回帰が正則化パラメータ(α)を固定値として扱うのに対し、BayesianRidge ではこれを確率的に扱い、データから学習します。
- ベイズ統計: このモデルは、係数および正則化パラメータに対する事前分布を仮定し、与えられたデータに基づいてこれらの事後分布を更新します。
- 自動的な正則化パラメータの調整:
BayesianRidgeは、データから正則化パラメータ(αとλ)の最適な値を自動的に推定します。これにより、正則化の強さがデータに適応します。 - 不確実性の推定: 予測に際して、不確実性(信頼区間)の推定が可能です。これは、ビジネス意思決定において重要な洞察を提供します。
- 多重共線性への対応: 他のリッジ回帰と同様に、
BayesianRidgeも多重共線性の問題を緩和します。
BayesianRidge モデルでは、ハイパーパラメータの調整が非常に限定的です。これは、モデル自体がデータに基づいてパラメータを学習するため、伝統的な回帰モデルのような多数のハイパーパラメータ調整が不要であるためです。しかし、以下のいくつかのハイパーパラメータが BayesianRidge には存在します。
| ハイパーパラメータ | 説明 | デフォルト値 |
|---|---|---|
| alpha_1 | αパラメータの事前分布に関連するハイパーパラメータ。正則化項の事前分布を制御。 | 1e-6 |
| alpha_2 | αパラメータの事前分布に関連するハイパーパラメータ。正則化項の事前分布を制御。 | 1e-6 |
| lambda_1 | λパラメータの事前分布に関連するハイパーパラメータ。正則化項の事前分布を制御。 | 1e-6 |
| lambda_2 | λパラメータの事前分布に関連するハイパーパラメータ。正則化項の事前分布を制御。 | 1e-6 |
BayesianRidge のモデルは、これらのハイパーパラメータをデフォルトの設定で適用することが多いです。
特定のデータセットやビジネスの問題に合わせ、これらのハイパーパラメータの微調整を行うことがあります。正則化パラメータの事前分布(alpha_1, alpha_2, lambda_1, lambda_2)を変更することで、モデルの正則化の度合いを間接的に調整することが可能です。
準備(モジュールとデータの読み込み)
必要なモジュールを読み込みます。
以下、コードです。
import numpy as np import pandas as pd import optuna from sklearn.model_selection import TimeSeriesSplit from sklearn.linear_model import BayesianRidge from mmm_functions import *
データセットを読み込みます。
以下、コードです。
# データセット読み込み
dataset = 'https://www.salesanalytics.co.jp/4zdt'
df = pd.read_csv(
dataset,
parse_dates=['Week'],
index_col='Week',
)
# 説明変数Xと目的変数yに分解
X = df.drop(columns=['Sales'])
y = df['Sales']
ハイパーパラメータをデフォルトのままMMM構築
ベイズリッジ回帰モデルでMMMを構築します。
以下、コードです。
# MMMの構築 model = BayesianRidge() trained_model,pred = train_and_evaluate_model(model, X, y)
以下、実行結果です。
RMSE: 284703.61107686715 MAE: 237742.09861380185 MAPE: 0.1214239166715309 R2: 0.7399745259359856
MMMの予測値(predicted)と実測値(actual)の推移をプロットします。
以下、コードです。
# 実測値と予測値の時系列推移 plot_actual_vs_predicted(y.index, y.values, pred.y.values, (0, 4e6))
以下、実行結果です。
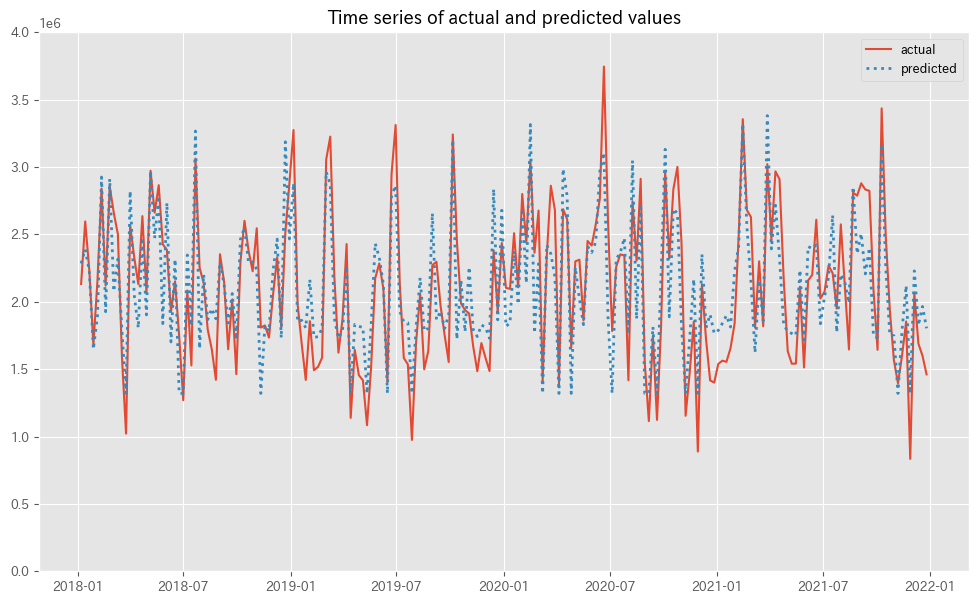
予測値を元に、貢献度を算定します。
以下、コードです。
# 貢献度の算出 contribution = calculate_and_plot_contribution(y, X, trained_model,(0, 4e6))
以下、実行結果です。
Base TVCM Newspaper Web Week 2018-01-07 1.231738e+06 900262.118555 0.000000 0.000000 2018-01-14 1.434416e+06 0.000000 530555.755636 631127.947451 2018-01-21 1.323517e+06 0.000000 420618.208734 492064.500677 2018-01-28 1.345917e+06 0.000000 334983.030412 0.000000 2018-02-04 1.503396e+06 0.000000 0.000000 652004.496623 ... ... ... ... ... 2021-11-28 8.339000e+05 0.000000 0.000000 0.000000 2021-12-05 1.222318e+06 0.000000 464512.061256 377869.537927 2021-12-12 1.221703e+06 0.000000 0.000000 467797.009130 2021-12-19 1.074473e+06 0.000000 525127.265842 0.000000 2021-12-26 1.069443e+06 0.000000 0.000000 391657.116149 [208 rows x 4 columns]
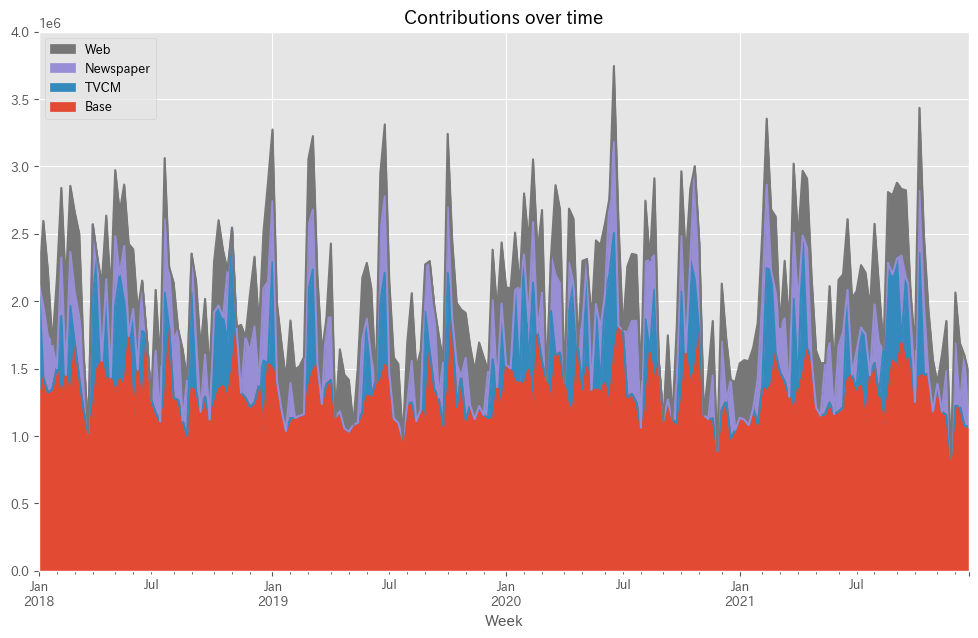
メディアの貢献度構成比を計算します。
以下、コードです。
# 貢献度構成比の算出 contribution_results = summarize_and_plot_contribution(contribution)
以下、実行結果です。
contribution ratio Base 2.742733e+08 0.625401 TVCM 4.289260e+07 0.097804 Newspaper 4.477142e+07 0.102088 Web 7.661877e+07 0.174707
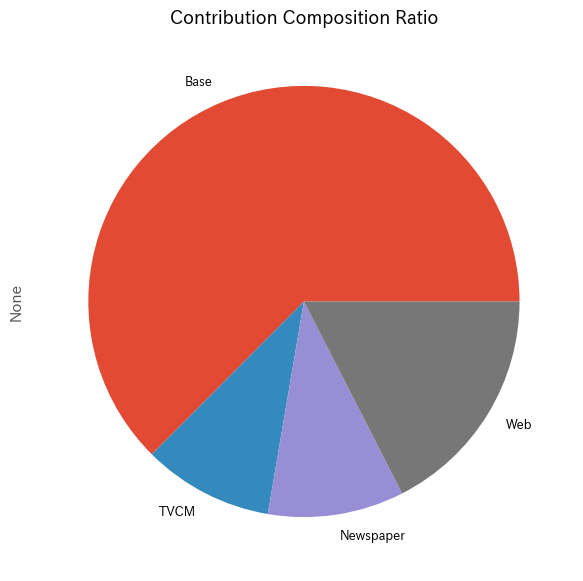
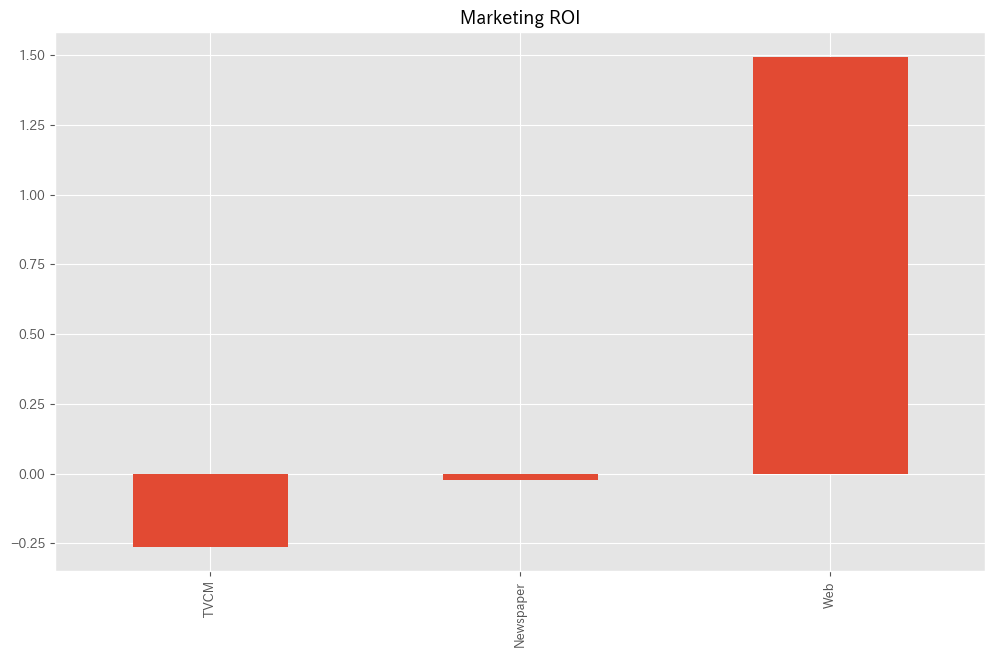
各メディアのマーケティングROIを計算します。
以下、コードです。
# マーケティングROIの算出 ROI = calculate_marketing_roi(X, contribution)
以下、実行結果です。
TVCM -0.262348 Newspaper -0.026416 Web 1.445595 dtype: float64
Optunaによるハイパーパラメータ調整しMMM構築
Optunaの目的関数を定義します。
以下、コードです。
# Optunaの目的関数の設定
def objective(trial):
# Optuna試行で使用するハイパーパラメータを提案
alpha_1 = trial.suggest_float('alpha_1', 1e-6, 1e-1, log=True)
alpha_2 = trial.suggest_float('alpha_2', 1e-6, 1e-1, log=True)
lambda_1 = trial.suggest_float('lambda_1', 1e-6, 1e-1, log=True)
lambda_2 = trial.suggest_float('lambda_2', 1e-6, 1e-1, log=True)
# BayesianRidgeモデルのインスタンス化
model = BayesianRidge(alpha_1=alpha_1, alpha_2=alpha_2, lambda_1=lambda_1, lambda_2=lambda_2)
# TimeSeriesSplitによるクロスバリデーション
tscv = TimeSeriesSplit(n_splits=5)
scores = cross_val_score(model, X, y, cv=tscv, scoring='neg_mean_squared_error')
rmse = np.mean([np.sqrt(-score) for score in scores])
# 平均RMSEを返す
return rmse
目的関数を最適化し、最適なハイパーパラメータを探索します。
以下、コードです。
# Optunaのスタディを作成し、目的関数を最適化
study = optuna.create_study(direction='minimize')
study.optimize(objective, n_trials=100)
# 最適なハイパーパラメータの表示
best_params = study.best_trial.params
print('Best trial:', best_params)
以下、実行結果です。
Best trial: {'alpha_1': 5.260520513928793e-06, 'alpha_2': 1.8760766342134607e-05, 'lambda_1': 3.311685675672814e-05, 'lambda_2': 0.0998139147571475}
最適なハイパーパラメータを使いMMMを構築します。
以下、コードです。
# MMMの構築 model = BayesianRidge(**best_params) trained_model,pred = train_and_evaluate_model(model, X, y)
以下、実行結果です。
RMSE: 284701.7591012649 MAE: 237740.135412738 MAPE: 0.12142040858167791 R2: 0.7399779088173327
MMMの予測値(predicted)と実測値(actual)の推移をプロットします。
以下、コードです。
# 実測値と予測値の時系列推移 plot_actual_vs_predicted(y.index, y.values, pred.y.values, (0, 4e6))
以下、実行結果です。
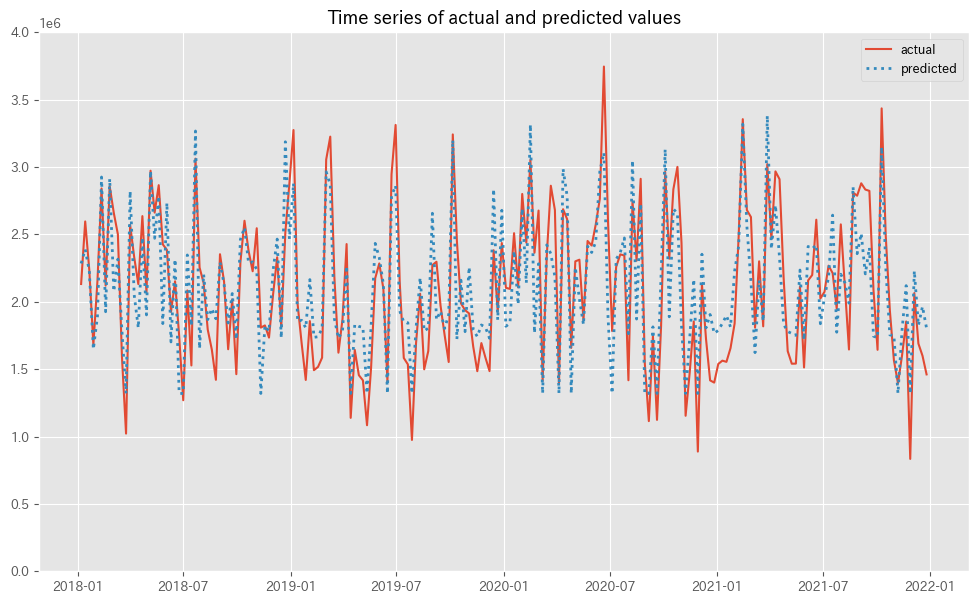
予測値を元に、貢献度を算定します。
以下、コードです。
# 貢献度の算出 contribution = calculate_and_plot_contribution(y, X, trained_model,(0, 4e6))
以下、実行結果です。
Base TVCM Newspaper Web Week 2018-01-07 1.231645e+06 900354.555793 0.000000 0.000000 2018-01-14 1.434080e+06 0.000000 530585.189944 631434.632050 2018-01-21 1.323235e+06 0.000000 420650.514470 492314.108874 2018-01-28 1.345839e+06 0.000000 335060.776479 0.000000 2018-02-04 1.503068e+06 0.000000 0.000000 652332.055718 ... ... ... ... ... 2021-11-28 8.339000e+05 0.000000 0.000000 0.000000 2021-12-05 1.222078e+06 0.000000 464555.163318 378067.261457 2021-12-12 1.221459e+06 0.000000 0.000000 468040.659232 2021-12-19 1.074370e+06 0.000000 525229.503658 0.000000 2021-12-26 1.069236e+06 0.000000 0.000000 391863.600980 [208 rows x 4 columns]
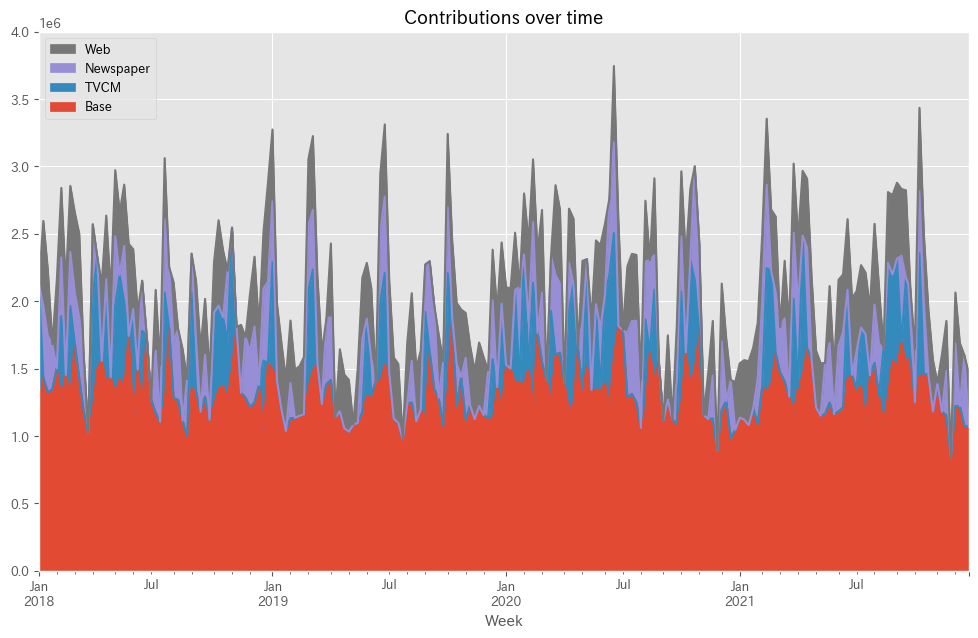
メディアの貢献度構成比を計算します。
以下、コードです。
# 貢献度構成比の算出 contribution_results = summarize_and_plot_contribution(contribution)
以下、実行結果です。
contribution ratio Base 2.742282e+08 0.625298 TVCM 4.289282e+07 0.097805 Newspaper 4.477657e+07 0.102100 Web 7.665847e+07 0.174797
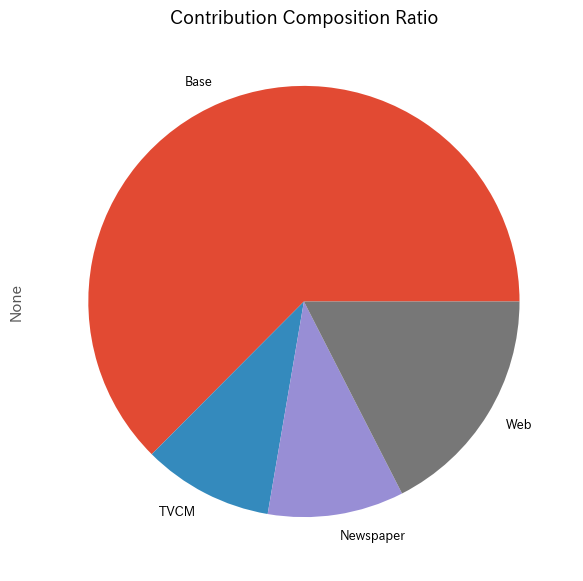
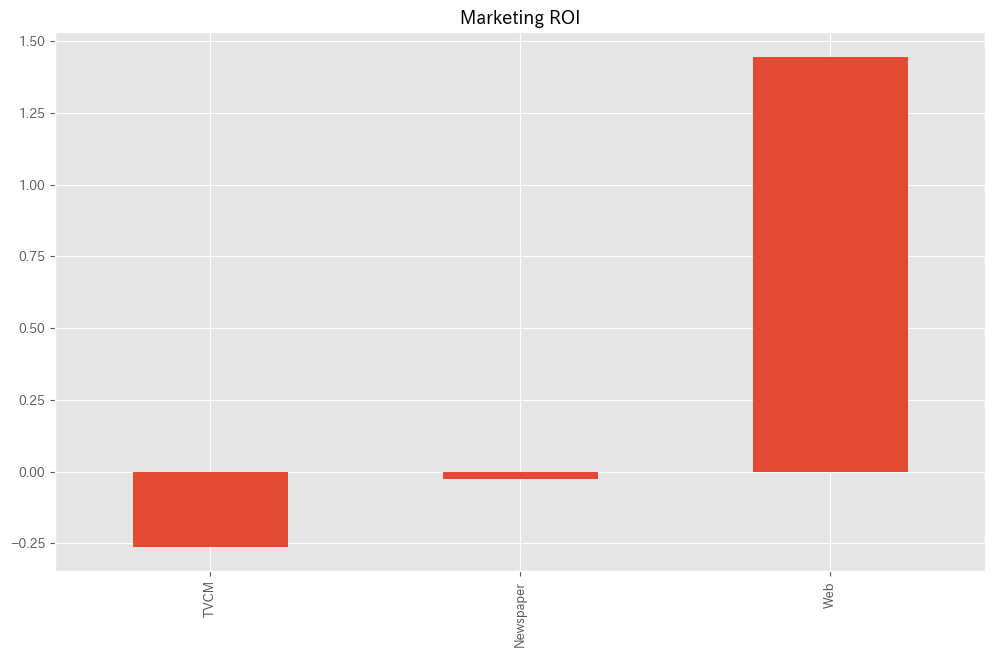
各メディアのマーケティングROIを計算します。
以下、コードです。
# マーケティングROIの算出 ROI = calculate_marketing_roi(X, contribution)
以下、実行結果です。
TVCM -0.262345 Newspaper -0.026304 Web 1.446862 dtype: float64
PLS回帰でMMM(パイプライン構築)
scikit-learn(sklearn)ライブラリーのPLSRegression(部分的最小2乗回帰、PLS回帰)でMMMを構築します。
PLS回帰モデルを構築するとき、説明変数に対し標準化処理(各変数からその平均値を引き標準偏差で割る)を実施します。
今回はPLSRegressionに備わっているスケーリング機能を使わずに、柔軟性を持たせるため、パイプライン(入力⇒標準化⇒PLS回帰⇒出力)を構築し対応します。
また、PLS回帰にはハイパーパラメータがありますので、それをOptunaでチューニングします。
今回は以下の2種類のモデルを作ります。
- ハイパーパラメータをデフォルトのまま(Optunaによるハイパラ調整なし)MMM構築
- Optunaによるハイパーパラメータ調整しMMM構築
PLS回帰とは?
scikit-learn(sklearn)ライブラリーの PLSRegression(部分的最小二乗回帰、Partial Least Squares Regression)は、高次元の説明変数を持つ場合や説明変数間で多重共線性がある場合に適した回帰分析手法です。
- 次元削減: PLSは、多数の説明変数を持つデータセットに対して、これらの変数の主要な成分(潜在変数)を抽出し、次元を削減します。
- 多重共線性の緩和: 多重共線性がある場合にも、PLSは相関関係のある変数群をまとめて扱うことで、この問題を緩和します。
- 変数の組み合わせ: PLSは、説明変数の組み合わせを利用して目的変数との関係をモデリングします。これにより、変数間の相互作用を考慮した予測が可能になります。
- 応用の幅広さ: PLSは、予測だけでなく、因果関係の探索やデータの構造解析にも利用できます。
もちろんです。scikit-learnのPLSRegression(部分的最小二乗回帰)モデルの主要なハイパーパラメータを一覧表にまとめます。
| ハイパーパラメータ | 説明 | デフォルト値 |
|---|---|---|
| n_components | 構築される潜在変数(成分)の数。モデルによって抽出される主要な成分の数を指定。 | 2 |
これらのハイパーパラメータは、PLSRegression モデルの性能と適合度に影響を与えるため、データの特性とビジネスの要件に合わせて慎重に選択する必要があります。特に n_components の選択は、モデルの複雑さと一般化能力のバランスを考慮する上で重要です。
準備(モジュールとデータの読み込み)
必要なモジュールを読み込みます。
以下、コードです。
import numpy as np import pandas as pd import optuna from sklearn.model_selection import TimeSeriesSplit from sklearn.pipeline import Pipeline from sklearn.preprocessing import StandardScaler from sklearn.cross_decomposition import PLSRegression from mmm_functions import *
データセットを読み込みます。
以下、コードです。
# データセット読み込み
dataset = 'https://www.salesanalytics.co.jp/4zdt'
df = pd.read_csv(
dataset,
parse_dates=['Week'],
index_col='Week',
)
# 説明変数Xと目的変数yに分解
X = df.drop(columns=['Sales'])
y = df['Sales']
ハイパーパラメータをデフォルトのままMMM構築
PLS回帰モデルを組み込んだパイプライン(入力⇒標準化⇒PLS回帰⇒出力)でMMMを構築します。
以下、コードです。
# MMMの構築
mmm_pipe = Pipeline([
('scaler', StandardScaler()),
('pls', PLSRegression())
])
trained_model, pred = train_and_evaluate_model(mmm_pipe, X, y)
このコードは、Pipelineを使用してマーケティングミックスモデル(MMM)を構築し、訓練および評価するプロセスを示しています。ここでのモデルは、特徴量の標準化と部分最小二乗回帰(PLSRegression)を組み合わせたものです。
- Pipelineの構築:
mmm_pipe = Pipeline([...]):Pipelineは、データ前処理とモデリングステップを一連のフローとして組み合わせるための便利な方法です。- ここでは、次の2つのステップが含まれています。
'scaler', StandardScaler():StandardScalerは、特徴量を標準化(平均0、標準偏差1に調整)するために使用されます。これにより、特徴量のスケールの違いがモデルの学習に影響を与えないようにします。'pls', PLSRegression():PLSRegressionは部分最小二乗回帰を行うためのモデルです。これは、特に多変量データでの予測に有用で、特徴量間の相関が高い場合や特徴量の数が多い場合に適しています。
- モデルの訓練と評価:
trained_model, pred = train_and_evaluate_model(mmm_pipe, X, y): 以前に定義されたtrain_and_evaluate_model関数を使用して、mmm_pipe(構築されたパイプライン)を訓練し、評価します。- この関数は、訓練データセット(
Xとy)に基づいてパイプラインを学習させ、予測を行い、パフォーマンス指標を計算します。
以下、実行結果です。
RMSE: 284690.67802959454 MAE: 237521.6103675306 MAPE: 0.12125403611197035 R2: 0.739998149418335
MMMの予測値(predicted)と実測値(actual)の推移をプロットします。
以下、コードです。
# 実測値と予測値の時系列推移 plot_actual_vs_predicted(y.index, y.values, pred.y.values, (0, 4e6))
以下、実行結果です。
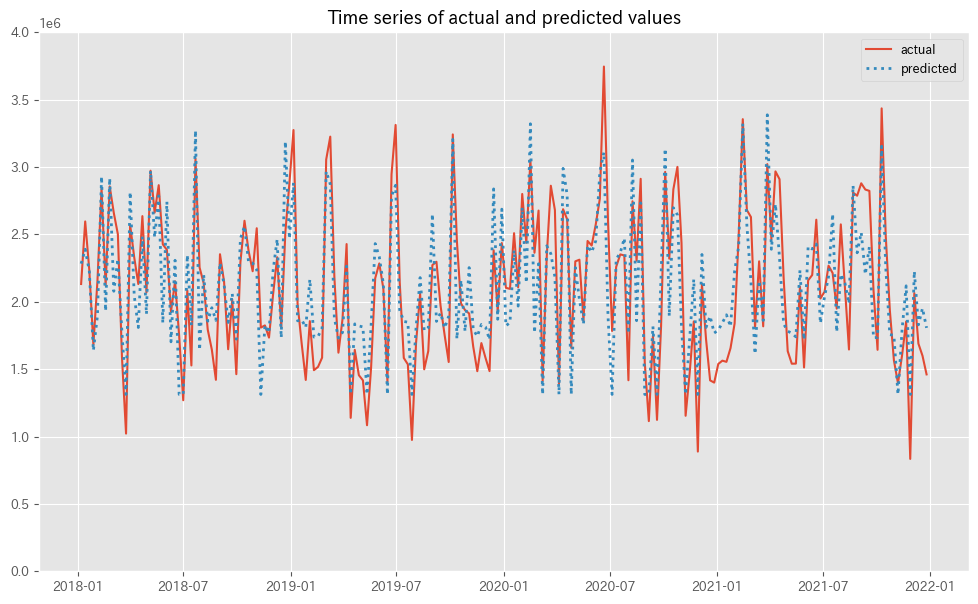
予測値を元に、貢献度を算定します。
以下、コードです。
# 貢献度の算出 contribution = calculate_and_plot_contribution(y, X, trained_model,(0, 4e6))
以下、実行結果です。
Base TVCM Newspaper Web Week 2018-01-07 1.225599e+06 906401.124046 0.000000 0.000000 2018-01-14 1.425565e+06 0.000000 525824.512387 644710.096009 2018-01-21 1.316132e+06 0.000000 417115.054450 502952.639226 2018-01-28 1.346659e+06 0.000000 334241.196676 0.000000 2018-02-04 1.490830e+06 0.000000 0.000000 664569.853457 ... ... ... ... ... 2021-11-28 8.339000e+05 0.000000 0.000000 0.000000 2021-12-05 1.216870e+06 0.000000 461163.249720 386666.760686 2021-12-12 1.212350e+06 0.000000 0.000000 477150.014935 2021-12-19 1.075449e+06 0.000000 524151.353241 0.000000 2021-12-26 1.061515e+06 0.000000 0.000000 399585.342198 [208 rows x 4 columns]
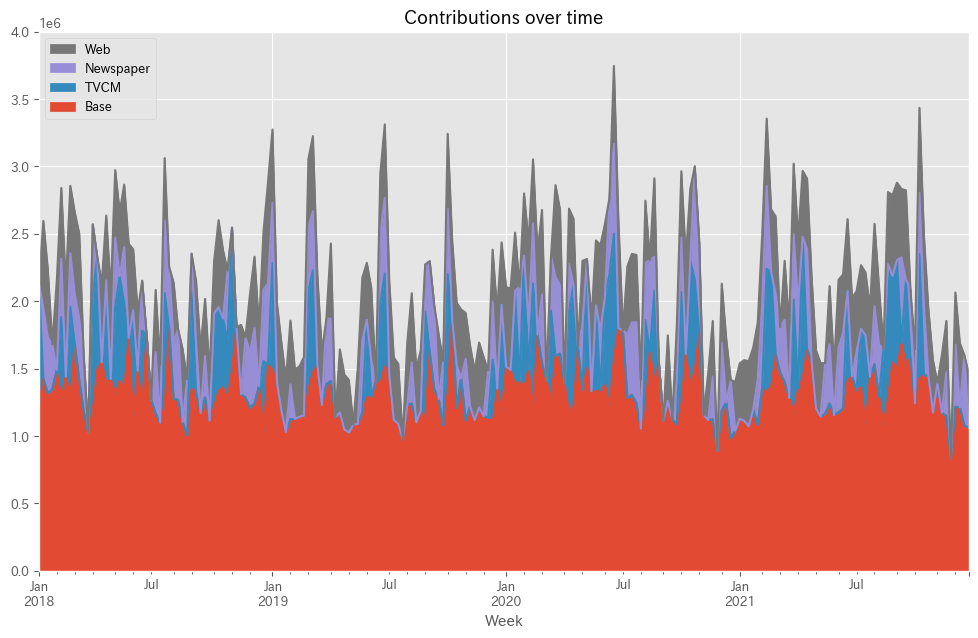
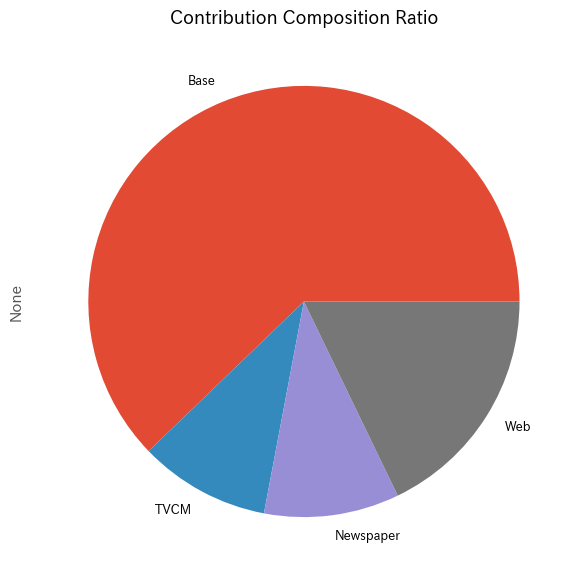
メディアの貢献度構成比を計算します。
以下、コードです。
# 貢献度構成比の算出 contribution_results = summarize_and_plot_contribution(contribution)
以下、実行結果です。
contribution ratio Base 2.727919e+08 0.622023 TVCM 4.310302e+07 0.098284 Newspaper 4.446063e+07 0.101380 Web 7.820058e+07 0.178314
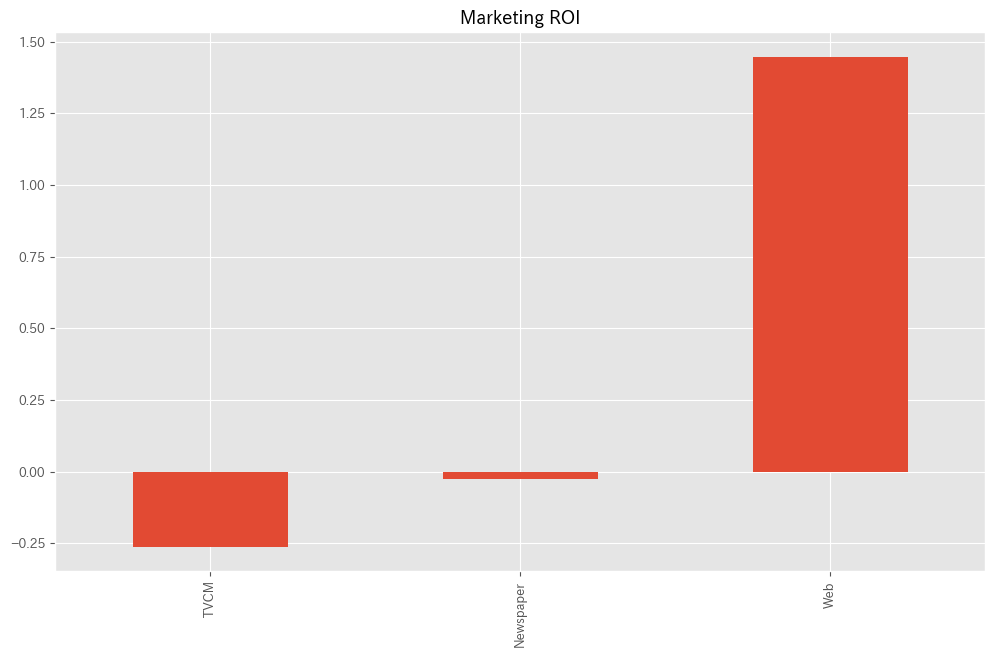
各メディアのマーケティングROIを計算します。
以下、コードです。
# マーケティングROIの算出 ROI = calculate_marketing_roi(X, contribution)
以下、実行結果です。
TVCM -0.258730 Newspaper -0.033174 Web 1.496085 dtype: float64
Optunaによるハイパーパラメータ調整しMMM構築
Optunaの目的関数を定義します。
以下、コードです。
# Optunaの目的関数の設定
def objective(trial):
# Optuna試行で使用するハイパーパラメータを提案
n_components = trial.suggest_int("n_components", 1, len(X.columns) )
# MMMパイプラインのインスタンス化
model = mmm_pipe.set_params(
pls__n_components=n_components
)
# TimeSeriesSplitによるクロスバリデーション
tscv = TimeSeriesSplit(n_splits=5)
scores = cross_val_score(model, X, y, cv=tscv, scoring='neg_mean_squared_error')
rmse = np.mean([np.sqrt(-score) for score in scores])
# 平均RMSEを返す
return rmse
目的関数を最適化し、最適なハイパーパラメータを探索します。
以下、コードです。
# Optunaのスタディを作成し、目的関数を最適化
study = optuna.create_study(direction='minimize')
study.optimize(objective, n_trials=100)
# 最適なハイパーパラメータの表示
best_params = study.best_trial.params
print('Best trial:', best_params)
以下、実行結果です。
Best trial: {'n_components': 3}
最適なハイパーパラメータを使いMMMを構築します。
以下、コードです。
# MMMの構築 model = mmm_pipe.set_params(pls__n_components=best_params["n_components"]) trained_model, pred = train_and_evaluate_model(model, X, y)
このコードは、Optunaで得られた最適なハイパーパラメータ(best_params)を用いて、マーケティングミックスモデル(MMM)を構築し、訓練および評価するプロセスを示しています。
- モデルの構築:
model = mmm_pipe.set_params(pls__n_components=best_params["n_components"]): この行では、以前に作成されたパイプラインmmm_pipe(StandardScalerとPLSRegressionを含む)のパラメータを設定しています。- 具体的には、部分最小二乗回帰(PLSRegression)モデルの
n_componentsパラメータを、最適化プロセスで特定された最適な値に設定しています。
- モデルの訓練と評価:
trained_model, pred = train_and_evaluate_model(model, X, y): この関数は、訓練データセット(Xとy)に基づいてモデルを学習させ、予測を行い、パフォーマンス指標を計算します。
以下、実行結果です。
RMSE: 284667.75543375366 MAE: 237679.0368036913 MAPE: 0.12129533117151893 R2: 0.7400400171566187
MMMの予測値(predicted)と実測値(actual)の推移をプロットします。
以下、コードです。
# 実測値と予測値の時系列推移 plot_actual_vs_predicted(y.index, y.values, pred.y.values, (0, 4e6))
以下、実行結果です。
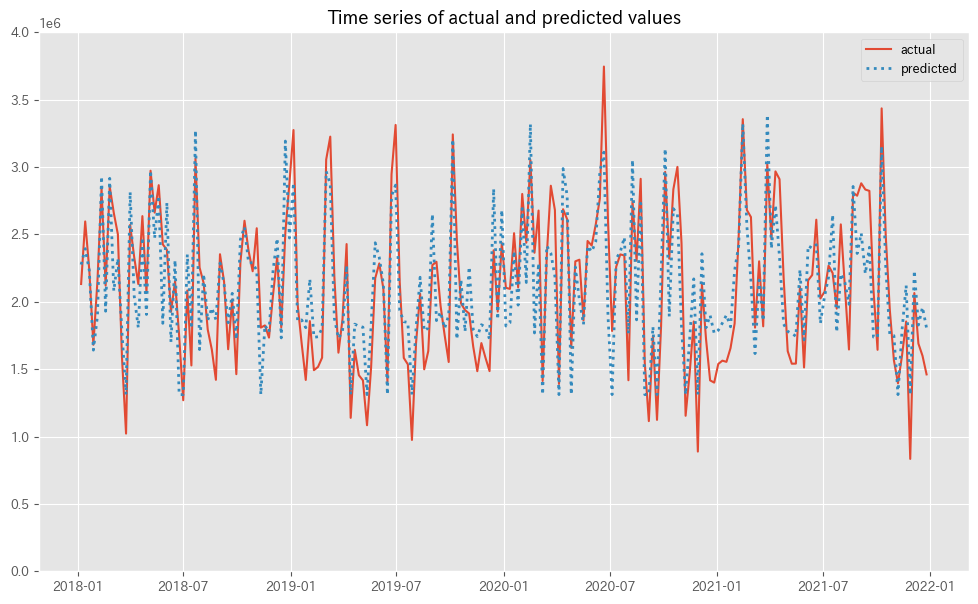
予測値を元に、貢献度を算定します。
以下、コードです。
# 貢献度の算出 contribution = calculate_and_plot_contribution(y, X, trained_model,(0, 4e6))
以下、実行結果です。
Base TVCM Newspaper Web Week 2018-01-07 1.228202e+06 903797.818513 0.000000 0.000000 2018-01-14 1.421614e+06 0.000000 531660.030809 642826.237428 2018-01-21 1.312771e+06 0.000000 421836.353351 501592.656646 2018-01-28 1.342945e+06 0.000000 337955.293145 0.000000 2018-02-04 1.490899e+06 0.000000 0.000000 664500.695310 ... ... ... ... ... 2021-11-28 8.339000e+05 0.000000 0.000000 0.000000 2021-12-05 1.213136e+06 0.000000 466142.340592 385422.124234 2021-12-12 1.212401e+06 0.000000 0.000000 477098.500910 2021-12-19 1.070570e+06 0.000000 529030.424496 0.000000 2021-12-26 1.061558e+06 0.000000 0.000000 399541.664901 [208 rows x 4 columns]
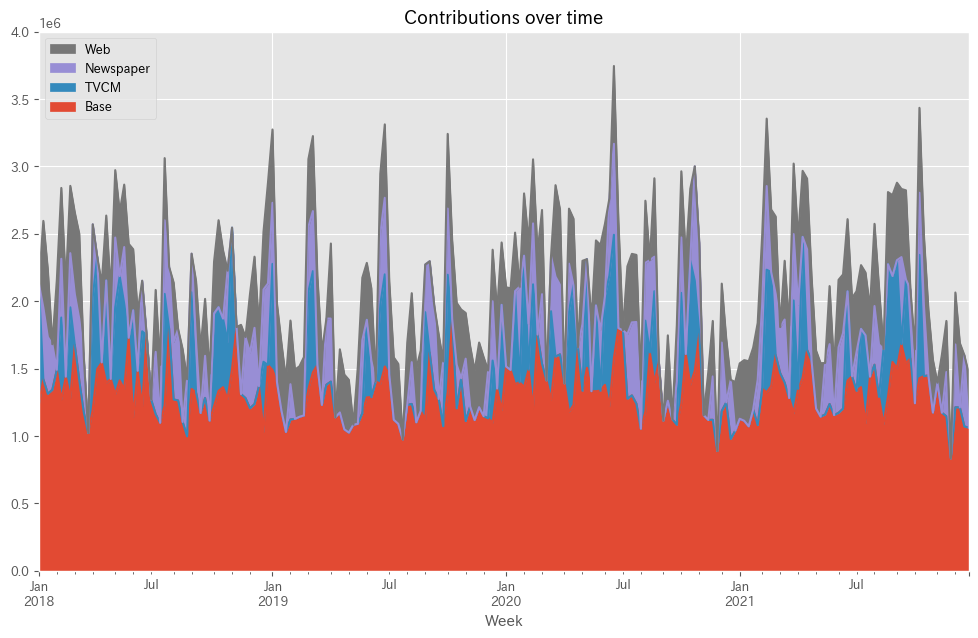
メディアの貢献度構成比を計算します。
以下、コードです。
# 貢献度構成比の算出 contribution_results = summarize_and_plot_contribution(contribution)
以下、実行結果です。
contribution ratio Base 2.725539e+08 0.621480 TVCM 4.290053e+07 0.097822 Newspaper 4.496719e+07 0.102535 Web 7.813451e+07 0.178163
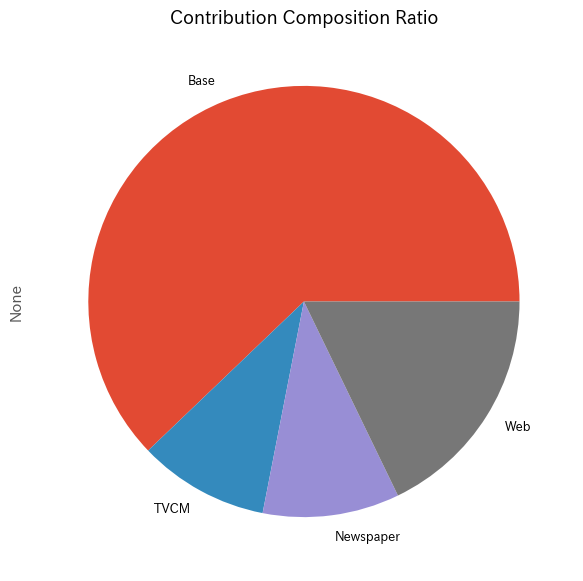
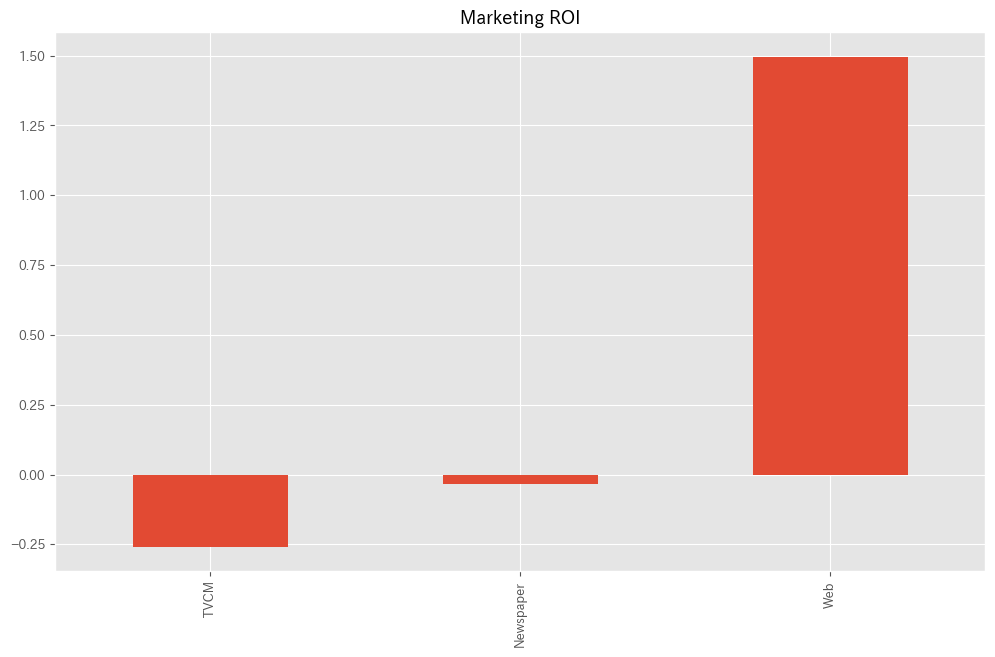
各メディアのマーケティングROIを計算します。
以下、コードです。
# マーケティングROIの算出 ROI = calculate_marketing_roi(X, contribution)
以下、実行結果です。
TVCM -0.262212 Newspaper -0.022159 Web 1.493975 dtype: float64
主成分回帰でMMM(パイプライン構築)
scikit-learn(sklearn)ライブラリーのPCAとLinearRegressionの組み合わせ(主成分回帰)でMMMを構築します。
主成分回帰モデルを構築するとき、説明変数に対し標準化処理を実施し、さらに主成分分析を実施します。
そのため、パイプライン(入力⇒標準化⇒主成分分析⇒線形回帰⇒出力)を構築し対応します。
また、主成分分析にはハイパーパラメータがありますので、それをOptunaでチューニングします。
今回は以下の2種類のモデルを作ります。
- ハイパーパラメータをデフォルトのまま(Optunaによるハイパラ調整なし)MMM構築
- Optunaによるハイパーパラメータ調整しMMM構築
主成分回帰とは?
scikit-learn(sklearn)ライブラリーでのPCA(主成分分析)とLinearRegression(線形回帰)の組み合わせは、主成分回帰(Principal Component Regression、PCR)として知られています。この手法は、高次元のデータセットで効果的に使用され、特に多重共線性の問題を緩和するのに役立ちます。
- PCAによる次元削減
- PCAは、データセットの主要な成分を抽出する次元削減技術です。データの変動を最大限に説明する成分(主成分)を抽出します。
- これにより、元の特徴空間がより少ない数の無相関成分に変換されます。
- 線形回帰モデルの適用
- 変換されたデータ(主成分)に対して
LinearRegressionを適用します。 - PCRは、主成分上での回帰を行うことで、元の特徴空間の多重共線性の問題を回避します。
- 変換されたデータ(主成分)に対して
PCRの適用には、PCAで使用する主成分の数を適切に選択することが重要です。主成分の数が少なすぎると重要な情報が失われ、多すぎると多重共線性の問題が解消されない可能性があります。したがって、PCRを使用する際には、クロスバリデーションなどを通じて最適な主成分の数を決定することが推奨されます。
準備(モジュールとデータの読み込み)
必要なモジュールを読み込みます。
以下、コードです。
import numpy as np import pandas as pd import optuna from sklearn.model_selection import TimeSeriesSplit from sklearn.pipeline import Pipeline from sklearn.preprocessing import StandardScaler from sklearn.decomposition import PCA from sklearn.linear_model import LinearRegression from mmm_functions import *
データセットを読み込みます。
以下、コードです。
# データセット読み込み
dataset = 'https://www.salesanalytics.co.jp/4zdt'
df = pd.read_csv(
dataset,
parse_dates=['Week'],
index_col='Week',
)
# 説明変数Xと目的変数yに分解
X = df.drop(columns=['Sales'])
y = df['Sales']
ハイパーパラメータをデフォルトのままMMM構築
主成分回帰モデルつまりパイプライン(入力⇒標準化⇒主成分分析⇒線形回帰⇒出力)でMMMを構築します。
以下、コードです。
# MMMの構築
mmm_pipe = Pipeline([
('scaler', StandardScaler()),
('pca', PCA()),
('regr', LinearRegression())
])
trained_model, pred = train_and_evaluate_model(mmm_pipe, X, y)
以下、実行結果です。
RMSE: 284667.75543375366 MAE: 237679.0368036913 MAPE: 0.12129533117151893 R2: 0.7400400171566187
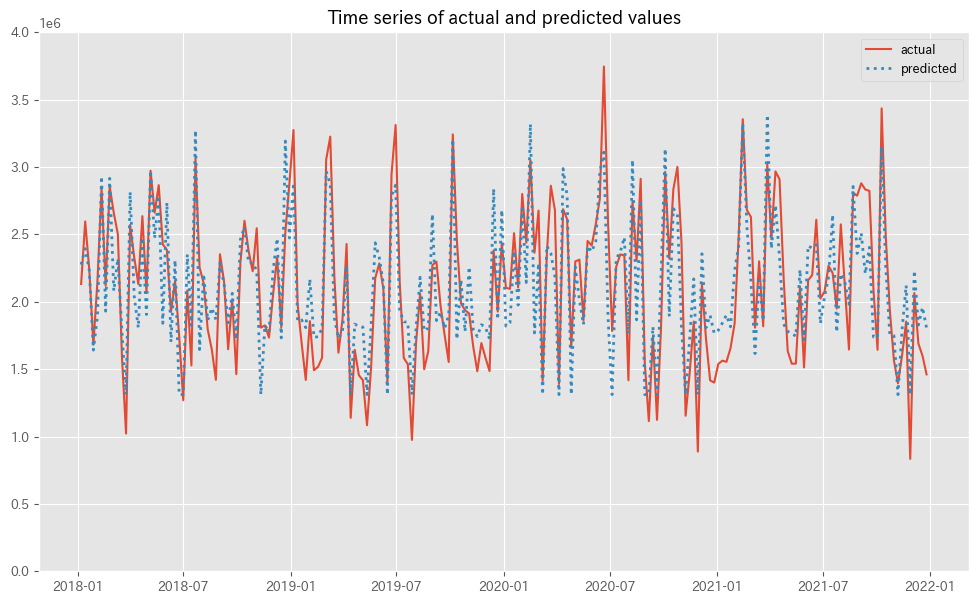
MMMの予測値(predicted)と実測値(actual)の推移をプロットします。
以下、コードです。
# 実測値と予測値の時系列推移 plot_actual_vs_predicted(y.index, y.values, pred.y.values, (0, 4e6))
以下、実行結果です。
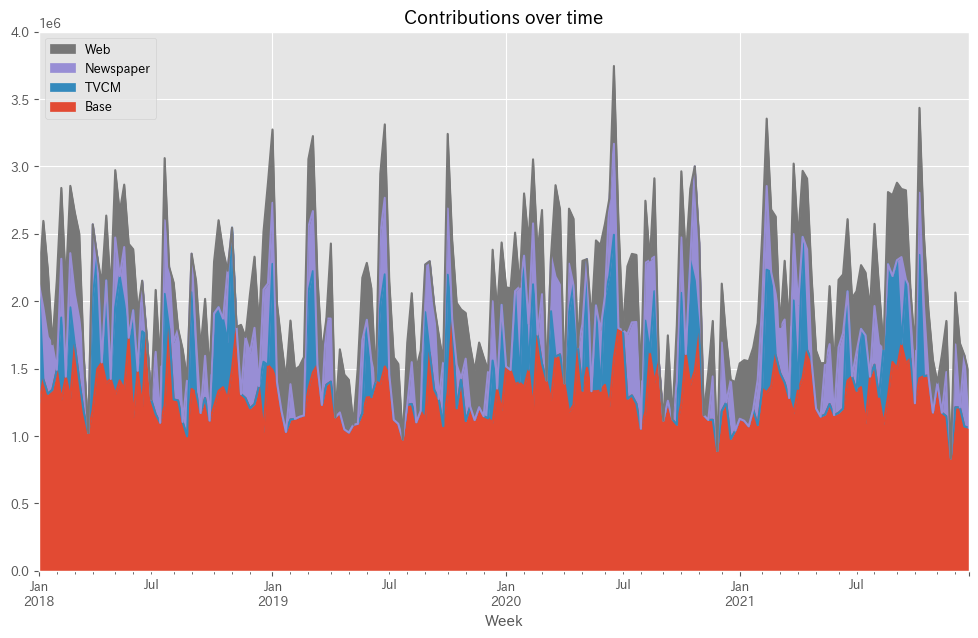
予測値を元に、貢献度を算定します。
以下、コードです。
# 貢献度の算出 contribution = calculate_and_plot_contribution(y, X, trained_model,(0, 4e6))
以下、実行結果です。
Base TVCM Newspaper Web Week 2018-01-07 1.228202e+06 903797.818513 0.000000 0.000000 2018-01-14 1.421614e+06 0.000000 531660.030809 642826.237428 2018-01-21 1.312771e+06 0.000000 421836.353351 501592.656646 2018-01-28 1.342945e+06 0.000000 337955.293145 0.000000 2018-02-04 1.490899e+06 0.000000 0.000000 664500.695310 ... ... ... ... ... 2021-11-28 8.339000e+05 0.000000 0.000000 0.000000 2021-12-05 1.213136e+06 0.000000 466142.340592 385422.124234 2021-12-12 1.212401e+06 0.000000 0.000000 477098.500910 2021-12-19 1.070570e+06 0.000000 529030.424496 0.000000 2021-12-26 1.061558e+06 0.000000 0.000000 399541.664901 [208 rows x 4 columns]
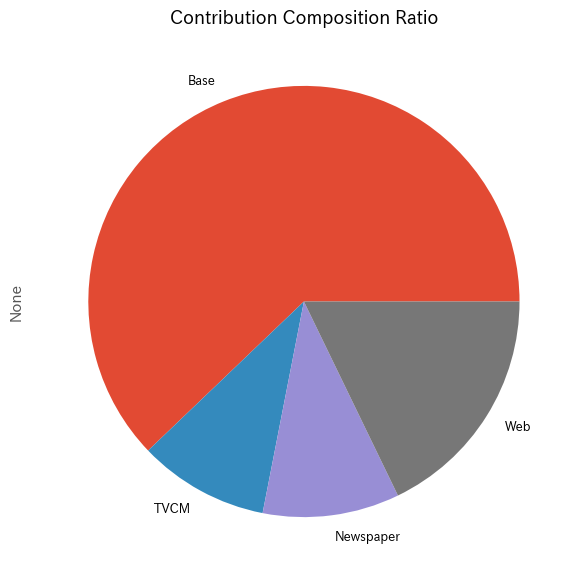
メディアの貢献度構成比を計算します。
以下、コードです。
# 貢献度構成比の算出 contribution_results = summarize_and_plot_contribution(contribution)
以下、実行結果です。
contribution ratio Base 2.725539e+08 0.621480 TVCM 4.290053e+07 0.097822 Newspaper 4.496719e+07 0.102535 Web 7.813451e+07 0.178163
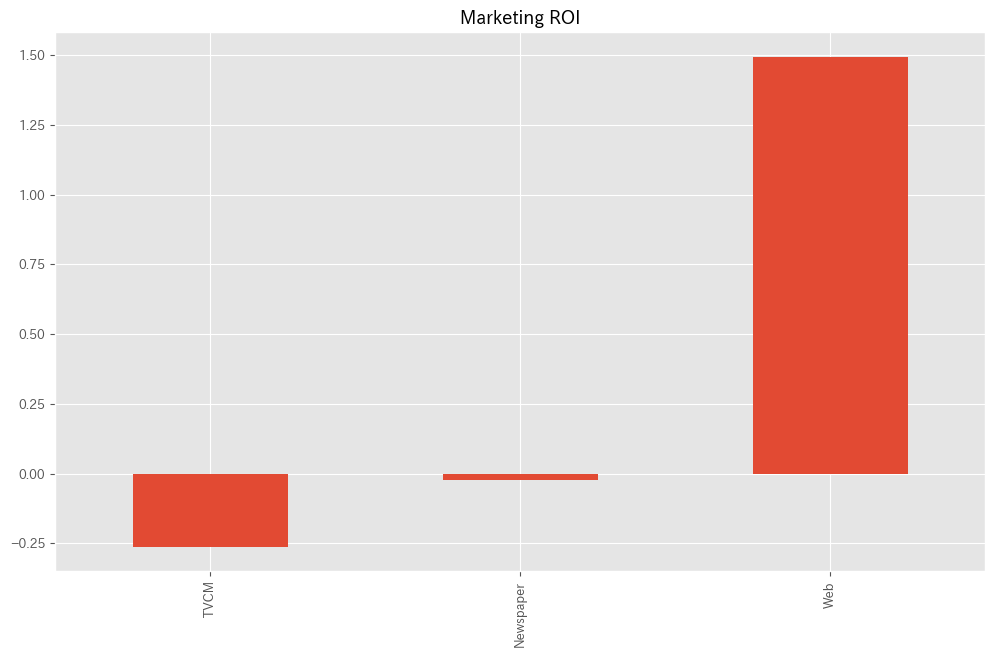
各メディアのマーケティングROIを計算します。
以下、コードです。
# マーケティングROIの算出 ROI = calculate_marketing_roi(X, contribution)
以下、実行結果です。
TVCM -0.262212 Newspaper -0.022159 Web 1.493975 dtype: float64
Optunaによるハイパーパラメータ調整しMMM構築
Optunaの目的関数を定義します。
以下、コードです。
# Optunaの目的関数の設定
def objective(trial):
# Optuna試行で使用するハイパーパラメータを提案
n_components = trial.suggest_int(
"n_components",
1, len(X.columns)
)
# MMMパイプラインのインスタンス化
model = mmm_pipe.set_params(
pca__n_components=n_components
)
# TimeSeriesSplitによるクロスバリデーション
tscv = TimeSeriesSplit(n_splits=5)
scores = cross_val_score(model, X, y, cv=tscv, scoring='neg_mean_squared_error')
rmse = np.mean([np.sqrt(-score) for score in scores])
# 平均RMSEを返す
return rmse
目的関数を最適化し、最適なハイパーパラメータを探索します。
以下、コードです。
# Optunaのスタディを作成し、目的関数を最適化
study = optuna.create_study(direction='minimize')
study.optimize(objective, n_trials=100)
# 最適なハイパーパラメータの表示
best_params = study.best_trial.params
print('Best trial:', best_params)
以下、実行結果です。
Best trial: {'n_components': 3}
最適なハイパーパラメータを使いMMMを構築します。
以下、コードです。
# MMMの構築 model = mmm_pipe.set_params(pca__n_components=best_params["n_components"]) trained_model, pred = train_and_evaluate_model(model, X, y)
以下、実行結果です。
RMSE: 284667.75543375366 MAE: 237679.0368036913 MAPE: 0.12129533117151893 R2: 0.7400400171566187
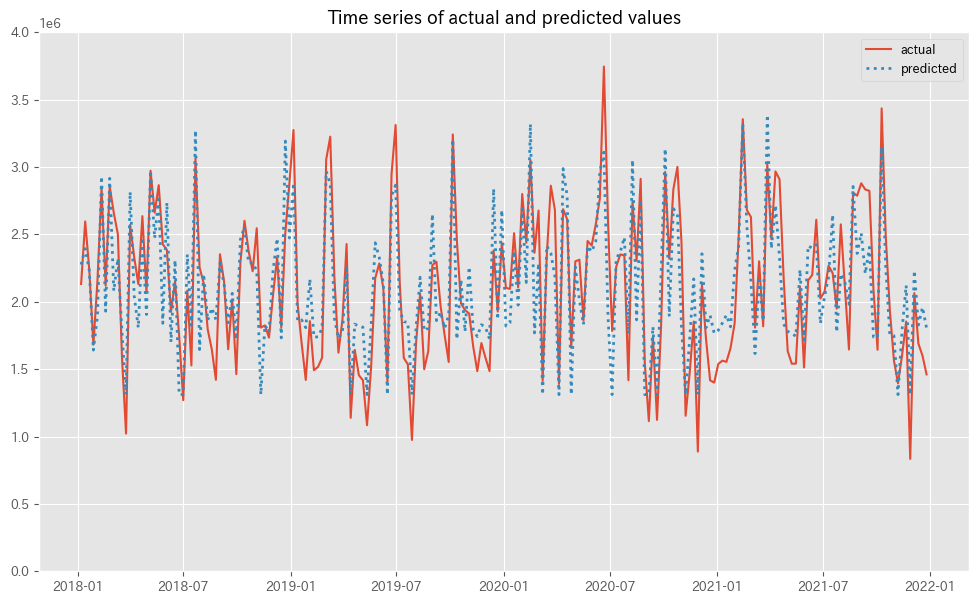
MMMの予測値(predicted)と実測値(actual)の推移をプロットします。
以下、コードです。
# 実測値と予測値の時系列推移 plot_actual_vs_predicted(y.index, y.values, pred.y.values, (0, 4e6))
以下、実行結果です。
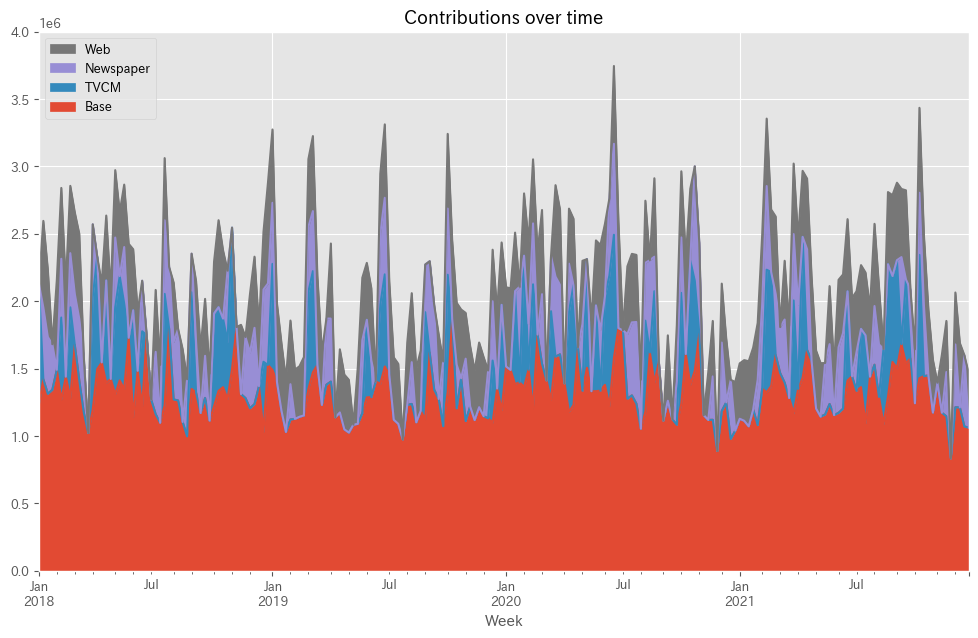
予測値を元に、貢献度を算定します。
以下、コードです。
# 貢献度の算出 contribution = calculate_and_plot_contribution(y, X, trained_model,(0, 4e6))
以下、実行結果です。
Base TVCM Newspaper Web Week 2018-01-07 1.228202e+06 903797.818513 0.000000 0.000000 2018-01-14 1.421614e+06 0.000000 531660.030809 642826.237428 2018-01-21 1.312771e+06 0.000000 421836.353351 501592.656646 2018-01-28 1.342945e+06 0.000000 337955.293145 0.000000 2018-02-04 1.490899e+06 0.000000 0.000000 664500.695310 ... ... ... ... ... 2021-11-28 8.339000e+05 0.000000 0.000000 0.000000 2021-12-05 1.213136e+06 0.000000 466142.340592 385422.124234 2021-12-12 1.212401e+06 0.000000 0.000000 477098.500910 2021-12-19 1.070570e+06 0.000000 529030.424496 0.000000 2021-12-26 1.061558e+06 0.000000 0.000000 399541.664901 [208 rows x 4 columns]
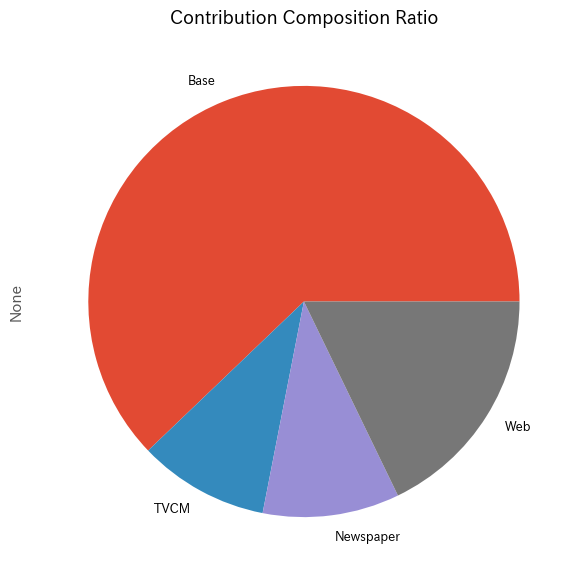
メディアの貢献度構成比を計算します。
以下、コードです。
# 貢献度構成比の算出 contribution_results = summarize_and_plot_contribution(contribution)
以下、実行結果です。
contribution ratio Base 2.725539e+08 0.621480 TVCM 4.290053e+07 0.097822 Newspaper 4.496719e+07 0.102535 Web 7.813451e+07 0.178163
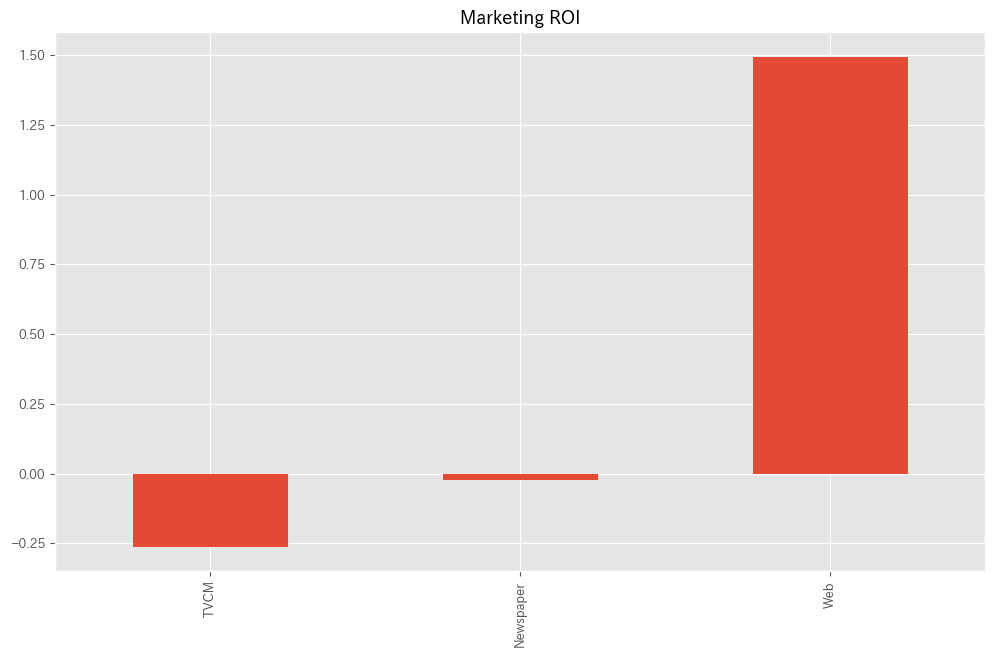
各メディアのマーケティングROIを計算します。
以下、コードです。
# マーケティングROIの算出 ROI = calculate_marketing_roi(X, contribution)
以下、実行結果です。
TVCM -0.262212 Newspaper -0.022159 Web 1.493975 dtype: float64
発展的話題②
– 線形系のモデル(推定器)の自動選択
線形系のモデル(推定器)には様々なものがあります。
今回は、以下の5つの線形系のモデルを、scikit-learn(sklearn)ライブラリーを使い構築しました。
LinearRegression:一般的な線形回帰モデルRidge:L2正則化を加えた線形回帰(リッジ回帰)BayesianRidge:ベイズ統計に基づいたリッジ回帰PLSRegression:部分的最小2乗回帰(Partial Least Squares Regression)- 主成分回帰:
PCAとLinearRegressionの組み合わせ
ここでは、Optunaを利用し、推定器選択と各推定器のハイパーパラメータチューニングも実施していきます。
単に、Optunaの目的関数の定義の中に、推定器選択とそのハイパーパラメータチューニングを組み込むだけです。
準備
必要なモジュールを読み込みます。
以下、コードです。
import numpy as np import pandas as pd from functools import partial import optuna from sklearn.model_selection import TimeSeriesSplit from sklearn.pipeline import Pipeline from sklearn.preprocessing import StandardScaler from sklearn.decomposition import PCA from sklearn.linear_model import LinearRegression from sklearn.linear_model import Ridge from sklearn.linear_model import BayesianRidge from sklearn.cross_decomposition import PLSRegression from mmm_functions import *
データセットを読み込みます。
以下、コードです。
# データセット読み込み
dataset = 'https://www.salesanalytics.co.jp/4zdt'
df = pd.read_csv(
dataset,
parse_dates=['Week'],
index_col='Week',
)
# 説明変数Xと目的変数yに分解
X = df.drop(columns=['Sales'])
y = df['Sales']
モデル(もしくはパイプライン)リスト
MMMとして利用するモデル(もしくはパイプライン)をリスト化します。
以下、コードです。
estimators = [
("LR", LinearRegression()),
("Ridge", Ridge()),
("BayesianRidge", BayesianRidge()),
("PLS", Pipeline([('scaler', StandardScaler()),
("Reg", PLSRegression())
])),
("PCR", Pipeline([('scaler', StandardScaler()),
("PCA", PCA()),
("Reg", LinearRegression())
]))
]
このコードは、複数の異なる推定器(estimators)を一覧として定義しています。ここで定義されている推定器は、MMM構築に利用するさまざまな種類の回帰モデルです。
- 線形回帰 (Linear Regression):
"LR", LinearRegression(): 標準的な線形回帰モデルです。特徴量とターゲット変数との間の線形関係をモデリングします。
- Ridge回帰:
"Ridge", Ridge(): Ridge回帰は線形回帰の一種で、正則化を含みます。正則化はモデルの複雑さを抑制し、過学習を防ぐのに役立ちます。
- ベイジアンRidge回帰:
"BayesianRidge", BayesianRidge(): ベイジアンアプローチを用いたRidge回帰です。モデルの重みに確率分布を使用し、不確実性をモデル化します。
- 部分最小二乗回帰 (PLS Regression):
"PLS", Pipeline([...]): 特徴量を標準化(StandardScaler)した後、PLSRegressionを適用するパイプラインです。PLSは、特徴量間の相関が高い場合に有用な手法です。
- 主成分回帰 (PCR: Principal Component Regression):
"PCR", Pipeline([...]): こちらもパイプラインで、特徴量を標準化した後、PCA(主成分分析)を適用し、その後線形回帰を行います。PCAは次元削減を行い、データの主要なパターンを抽出します。
これらの推定器は、それぞれ異なる特性を持ち、特定のデータセットや問題に対して異なるパフォーマンスを示す可能性があります。このように複数のモデルを定義し比較することは、最も適したモデルを選択する際に有用です。
Optunaで自動探索&チューニング
Optunaの目的関数の定義の中に、推定器選択とそのハイパーパラメータチューニングを組み込みます。
以下、コードです。
def objective(trial, X, y, estimators):
# 推定器(もしくはパイプライン)の選択
estimator_name = trial.suggest_categorical("estimator", [name for name, _ in estimators])
estimator = next((est for name, est in estimators if name == estimator_name), None)
if estimator_name == "LR":
pass
if estimator_name == "Ridge":
alpha = trial.suggest_loguniform("alpha_" + estimator_name, 0.01, 10)
estimator.set_params(alpha=alpha)
if estimator_name == "BayesianRidge":
alpha_1 = trial.suggest_loguniform("alpha_1_" + estimator_name, 1e-6, 1e-3)
alpha_2 = trial.suggest_loguniform("alpha_2_" + estimator_name, 1e-6, 1e-3)
lambda_1 = trial.suggest_loguniform("lambda_1_" + estimator_name, 1e-6, 1e-3)
lambda_2 = trial.suggest_loguniform("lambda_2_" + estimator_name, 1e-6, 1e-3)
estimator.set_params(
alpha_1=alpha_1, alpha_2=alpha_2, lambda_1=lambda_1, lambda_2=lambda_2)
if estimator_name == "PLS":
n_comp = trial.suggest_int("n_comp_" + estimator_name, 1, X.shape[1])
estimator.set_params(Reg__n_components=n_comp)
if estimator_name == "PCR":
n_comp = trial.suggest_int("n_comp_" + estimator_name, 1, X.shape[1])
estimator.set_params(PCA__n_components=n_comp)
# TimeSeriesSplitによるクロスバリデーション
tscv = TimeSeriesSplit(n_splits=5)
scores = cross_val_score(estimator, X, y, cv=tscv, scoring='neg_mean_squared_error')
rmse = np.mean([np.sqrt(-score) for score in scores])
# 平均RMSEを返す
return rmse
このコードは、Optunaを使用して複数の推定器(回帰モデル)の中から最適なモデルとそのハイパーパラメータを選択するための目的関数objectiveを定義しています。
- 推定器の選択:
estimator_name = trial.suggest_categorical(...): Optunaの試行で使用する推定器の名前を選択します。選択肢は、事前に定義されたestimatorsリストから取得されます。estimator = next(...): 選択された名前に対応する推定器(モデル)をestimatorsリストから取得します。
- ハイパーパラメータの設定:
- 各推定器に応じて、Optunaを使ってハイパーパラメータを提案し、それらを推定器に設定します。
- 例えば、Ridge回帰の
alpha、ベイジアンRidgeのalpha_1,alpha_2,lambda_1,lambda_2、PLSとPCRの成分数n_componentsなどです。
- 時系列クロスバリデーション:
tscv = TimeSeriesSplit(n_splits=5): 5つのスプリットで時系列クロスバリデーションを設定します。- クロスバリデーションの各スプリットで、モデルを訓練セットで学習させ、テストセットで予測を行います。
- RMSEの計算:
- 各スプリットでのRMSEを計算し、リストに追加します。
score = np.mean(rmse_list): RMSEの平均値を計算します。
- 戻り値:
- 最終的なスコア(平均RMSE)を返します。Optunaはこのスコアを最小化するようにモデルとハイパーパラメータの選択を行います。
この関数を使用することで、複数の異なる回帰モデルの中から最も時系列データに適したモデルを選択し、そのモデルのハイパーパラメータを最適化することができます。これは、特に複雑な時系列データを扱う場合に有効なアプローチです。時系列クロスバリデーションを用いて各モデルの平均RMSE(平均二乗誤差の平方根)を計算しています。
この目的関数を使い、探索を実行、その結果を出力します。
以下、コードです。
# Optunaのスタディを作成し、目的関数を最適化
study = optuna.create_study(direction='minimize')
objective_with_data = partial(objective, X=X, y=y, estimators=estimators)
study.optimize(objective_with_data, n_trials=1000)
# 最適なハイパーパラメータの表示
print("Best trial:")
trial = study.best_trial
print(f"Value: {trial.value}")
print("Params: ")
for key, value in trial.params.items():
print(f"{key}: {value}")
このコードは、Optunaハイパーパラメータ最適化ライブラリを使用して、的関数を最適化し、最適なハイパーパラメータを見つけ出すプロセスを示しています。
- Optunaのスタディ作成
optuna.create_study(direction='minimize'): ここで新しいスタディ(最適化のセッション)を作成します。direction='minimize'は、目的関数の値を最小化することを目指すことを意味します。逆に、最大化したい場合は'maximize'を指定します。- このスタディは、試行錯誤を通じて最適なハイパーパラメータセットを見つけ出します。
- 目的関数の準備
partial(objective, X=X, y=y, estimators=estimators):- ハイパーパラメータを探索する
study.optimize()メソッドを使用する際、目的関数(この場合はobjective関数)が必要となります。しかし、objective関数は追加のデータセット(X,y)と推定器のリスト(estimators)を必要とするため、直接study.optimize()に渡すことはできません。 - そこで
partialを使用して、これらのデータセット(Xとy)を固定した新しい関数objective_with_dataを生成し、この関数をstudy.optimize()に渡します。partialは関数の一部の引数を固定するために使用されます。
- ハイパーパラメータを探索する
- 最適化プロセス
study.optimize(objective_with_data, n_trials=1000):- ここで、準備した目的関数を使って最適化プロセスを開始します。
n_trials=1000は、最適化プロセスが1000回の試行を行うことを意味します。- 各試行では、Optunaが新しいハイパーパラメータのセットを提案し、目的関数がこれを評価してスコアを返します。
- 最適なハイパーパラメータの表示
study.best_trial: 最適化プロセスの後、最も良い結果を示した試行(best trial)を取得します。これは、目的関数が最小の値を返した試行です。trial.value: 最適な試行で得られた目的関数の値を表示します。trial.params.items(): 最適な試行で使用されたハイパーパラメータのセットを取得し、それぞれのキー(パラメータ名)と値を表示します。
このコードを通じて、MMMモデルの性能を最適化するためのハイパーパラメータを効率的に探索し、選択することができます。
以下、実行結果です。
Best trial: {'estimator': 'Ridge', 'alpha_Ridge': 9.997585432122557}
Ridge回帰(
MMM構築
Optunaで最適な推定器とハイパーパラメータを得られたら、MMMを構築します。
そのための関数(最適なハイパーパラメータを用いてインスタンスを生成)を作成します。
以下、コードです。
def create_model_from_trial(trial, estimators):
"""
最適化Trialからモデルを構築して学習する。
Parameters:
trial: 最適化なトライアル(Optunaの結果)
estimators: 推定器リスト
Returns:
学習済みのモデル
"""
best_params = trial.best_trial.params
estimator_name = best_params["estimator"]
estimator = next((est for name, est in estimators if name == estimator_name), None)
# パラメータの設定
param_keys = [key for key in best_params if key.startswith(estimator_name)]
params = {key.split(f"{estimator_name}_")[1]: best_params[key] for key in param_keys}
estimator.set_params(**params)
return estimator
このコードは、Optunaによるハイパーパラメータ最適化の結果から特定のモデルのインスタンスを生成する関数create_model_from_trialを定義しています。この関数は、最適化プロセス(Trial)の結果を使用して、選択されたモデルに最適なハイパーパラメータを設定します。
- 関数の定義:
- 関数は、Optunaの
trial(最適化された試行の結果)とestimators(推定器のリスト)を引数として受け取ります。
- 関数は、Optunaの
- 最適なパラメータの取得:
best_params = trial.best_trial.params: 最適化された試行から最適なパラメータを取得します。estimator_name = best_params["estimator"]: 選択された推定器の名前を取得します。
- 推定器の取得:
estimator = next(...):選択された名前に対応する推定器をestimatorsリストから取得します。
- ハイパーパラメータの設定:
param_keys = [key for key in best_params if key.startswith(estimator_name)]: 選択された推定器に関連するハイパーパラメータのキーを抽出します。params = {...}: 抽出されたキーに対応する最適なパラメータを辞書形式で取得します。estimator.set_params(**params): 選択された推定器に最適なパラメータを設定します。
- 戻り値:
- 関数は設定されたパラメータを持つ推定器を返します。
- この推定器は、訓練データに対して別途
fitメソッドを呼び出すことで学習を行う必要があります。
最適なハイパーパラメータを使いMMMを構築します。
以下、コードです。
# MMMの構築 model = create_model_from_trial(study, estimators) trained_model, pred = train_and_evaluate_model(model, X, y)
以下、実行結果です。
RMSE: 284667.75543375366 MAE: 237679.03680369648 MAPE: 0.12129533117154913 R2: 0.7400400171566186
MMMの予測値(predicted)と実測値(actual)の推移をプロットします。
以下、コードです。
# 実測値と予測値の時系列推移 plot_actual_vs_predicted(y.index, y.values, pred.y.values, (0, 4e6))
以下、実行結果です。
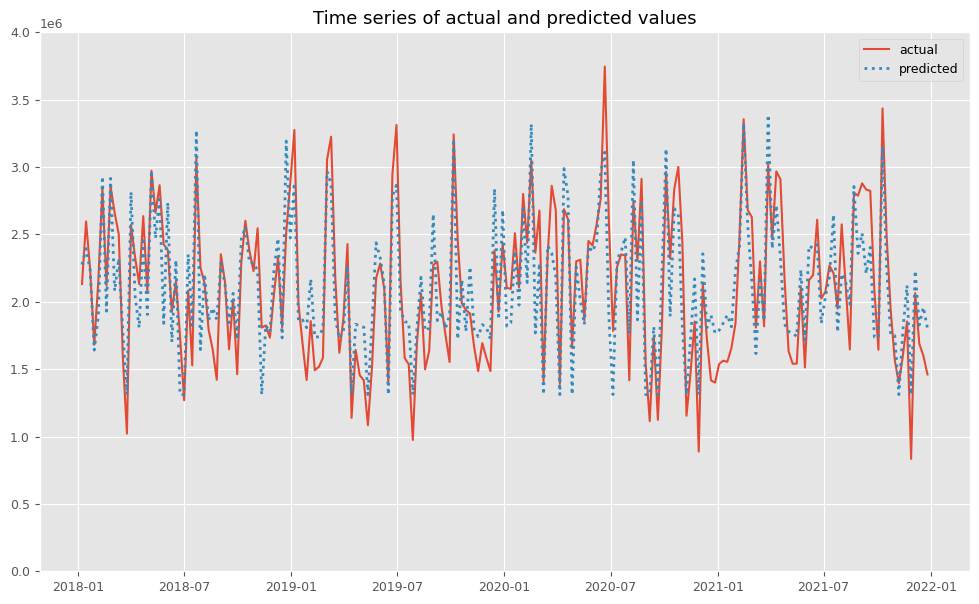
後処理(結果の出力)
MMMを構築したら、貢献度やマーケティングROIなどを計算していきます。
先ずは、貢献度を計算します。
以下、コードです。
# 貢献度の算出 contribution = calculate_and_plot_contribution(y, X, trained_model,(0, 4e6))
以下、実行結果です。
Base TVCM Newspaper Web Week 2018-01-07 1.228202e+06 903797.818512 0.000000 0.000000 2018-01-14 1.421614e+06 0.000000 531660.030809 642826.237425 2018-01-21 1.312771e+06 0.000000 421836.353350 501592.656643 2018-01-28 1.342945e+06 0.000000 337955.293144 0.000000 2018-02-04 1.490899e+06 0.000000 0.000000 664500.695306 ... ... ... ... ... 2021-11-28 8.339000e+05 0.000000 0.000000 0.000000 2021-12-05 1.213136e+06 0.000000 466142.340591 385422.124232 2021-12-12 1.212401e+06 0.000000 0.000000 477098.500907 2021-12-19 1.070570e+06 0.000000 529030.424495 0.000000 2021-12-26 1.061558e+06 0.000000 0.000000 399541.664899 [208 rows x 4 columns]
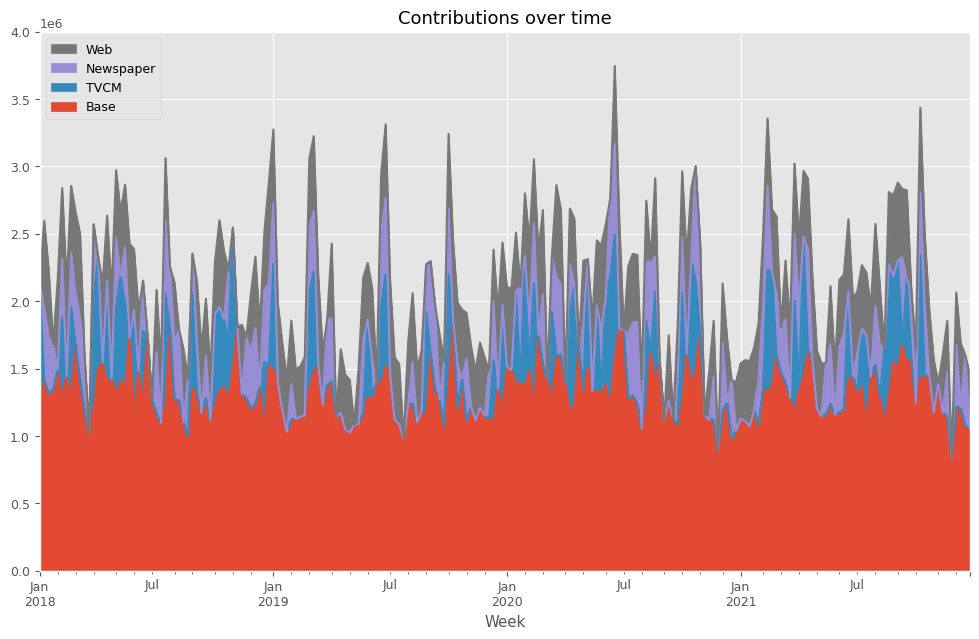
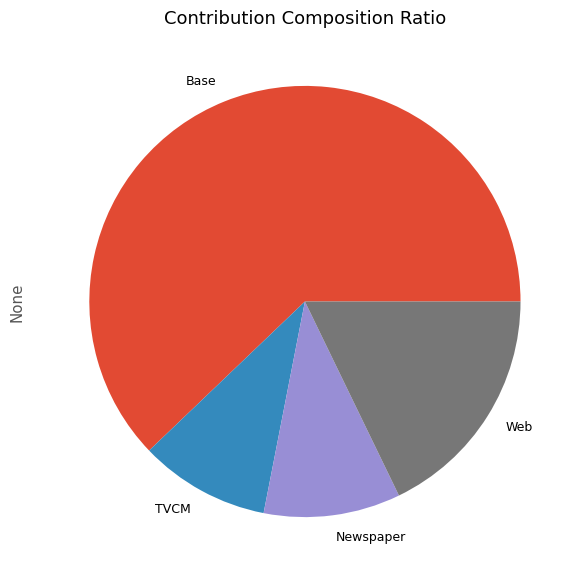
次に、貢献度の割合を計算します。
以下、コードです。
# 貢献度構成比の算出 contribution_results = summarize_and_plot_contribution(contribution)
以下、実行結果です。
contribution ratio Base 2.725539e+08 0.621480 TVCM 4.290053e+07 0.097822 Newspaper 4.496719e+07 0.102535 Web 7.813451e+07 0.178163
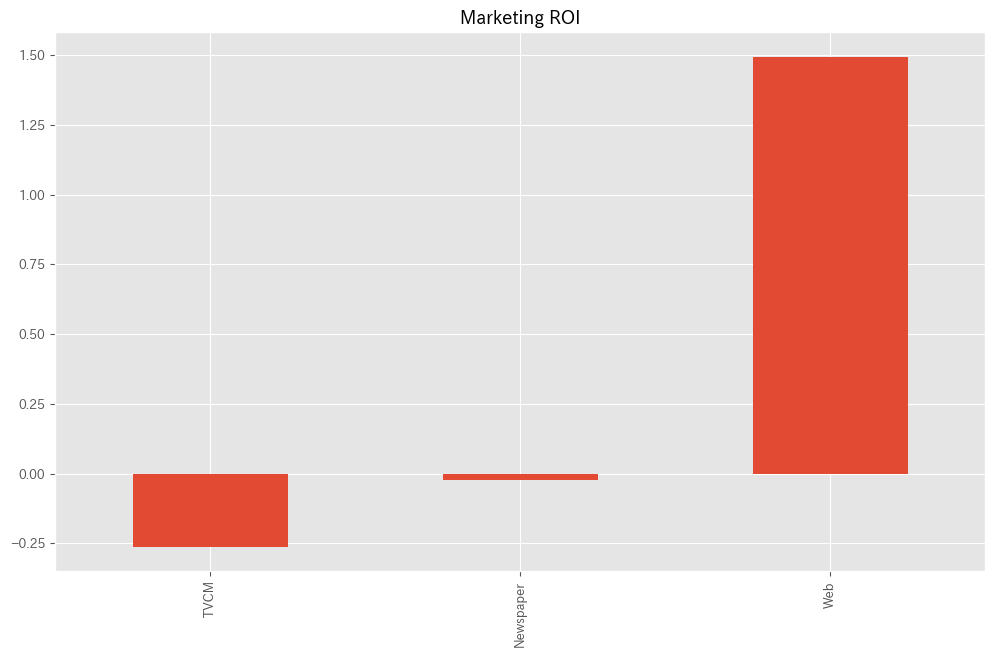
最後に、各メディアのマーケティングROIを計算します。
以下、コードです。
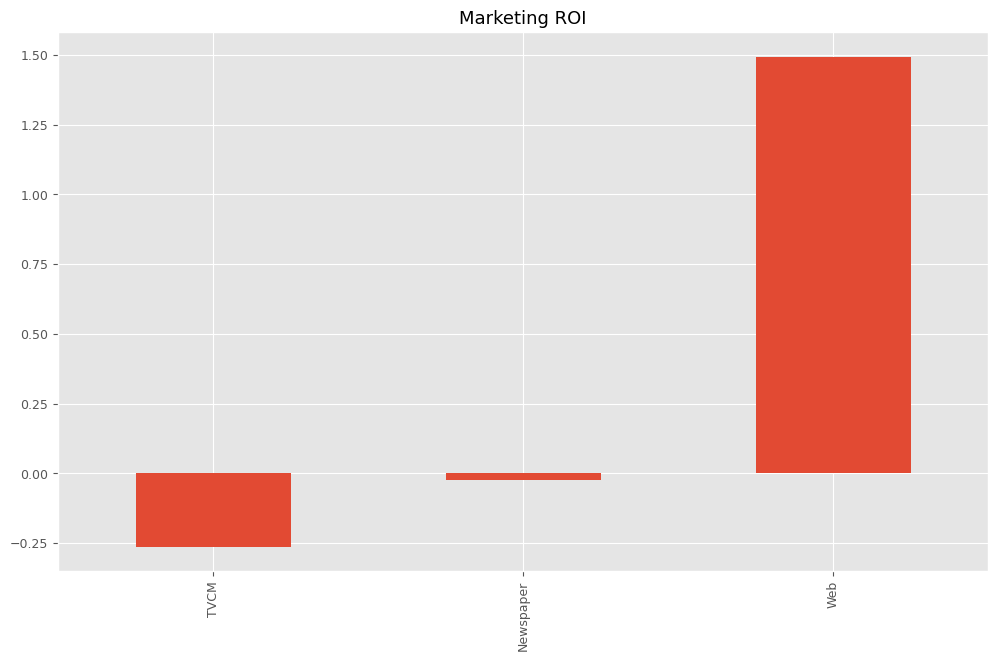
# マーケティングROIの算出 ROI = calculate_marketing_roi(X, contribution)
以下、実行結果です。
TVCM -0.262212 Newspaper -0.022159 Web 1.493975 dtype: float64
まとめ
今回は、「線形回帰系モデルでのMMM構築」というお話しをしました。
線形回帰系のモデルには色々なものあります。
広告販促系のデータは、お互いの相関関係が強い傾向(同じ時期に集中し広告投下など)があり、多重共線性問題が起こる可能性が低くはありません。そのような場合には、RidgeやBayesianRidge などのRidge(リッジ)回帰系のモデルがいいでしょう。
大規模なデータセットの場合には主成分分析(PCA)とSGDRegressorを組み合わせると良いかと思います。
ただし、今回紹介したモデルには、重大な欠陥があります。
それはアドストック(キャリーオーバー効果や飽和効果)が考慮されていないことです。
通常のMMMは、アドストックが考慮されます。ただし、アドストックにも色々なアドストックがあります。
次回は、アドストックについて取り上げます。
PythonによるMMM(マーケティングミックスモデリング)とビジネス活用- 振返り分析・線形回帰系モデル編(その2)-シンプルなアドストック付き線形回帰系MMM

