データを活用したマーケティング戦略は、ビジネスの成功に不可欠です。その中心に位置するのが、マーケティングミックスモデリング（MMM）です。

マーケティングミックスモデリング（MMM）は、過去のデータを分析する「振り返り分析」と未来のトレンドを予測する「近未来分析」の両方で有効に活用される強力なツールです。

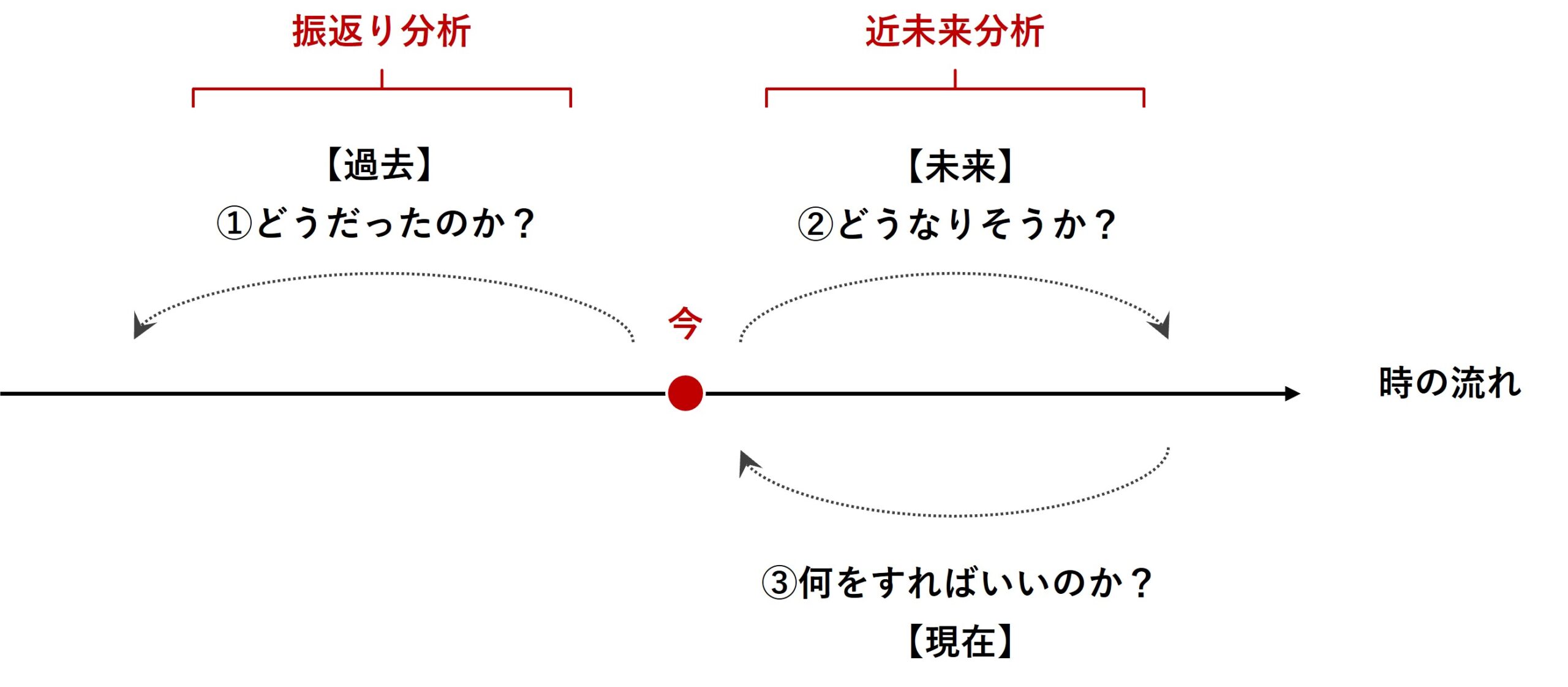
通常のMMMは、アドストック（Ad Stock）が考慮されます。

ここで言うアドストック（Ad Stock）とは、キャリーオーバー効果や飽和効果のことです。

例えば……

• キャリーオーバー効果とは「その日の広告の効果が次の日以降も継続していること」
• 飽和効果とは「その広告の投下量の増加が売上などにもたらす効果が、ある限界に達すると、それ以上の増加がほとんどないこと」

 

アドストック（Ad Stock）にも色々なアドストック（Ad Stock）があります。

前回は、シンプルなアドストックを組み込んだMMMを取り上げました。

PythonによるMMM（マーケティングミックスモデリング）とビジネス活用－ 振返り分析編（その3）：シンプルなアドストック付き線形回帰系MMM －

 

前回は、以下のようなシンプルなアドストック（上がキャリオーバー効果関数、下が飽和関数）を組み込みました。

 

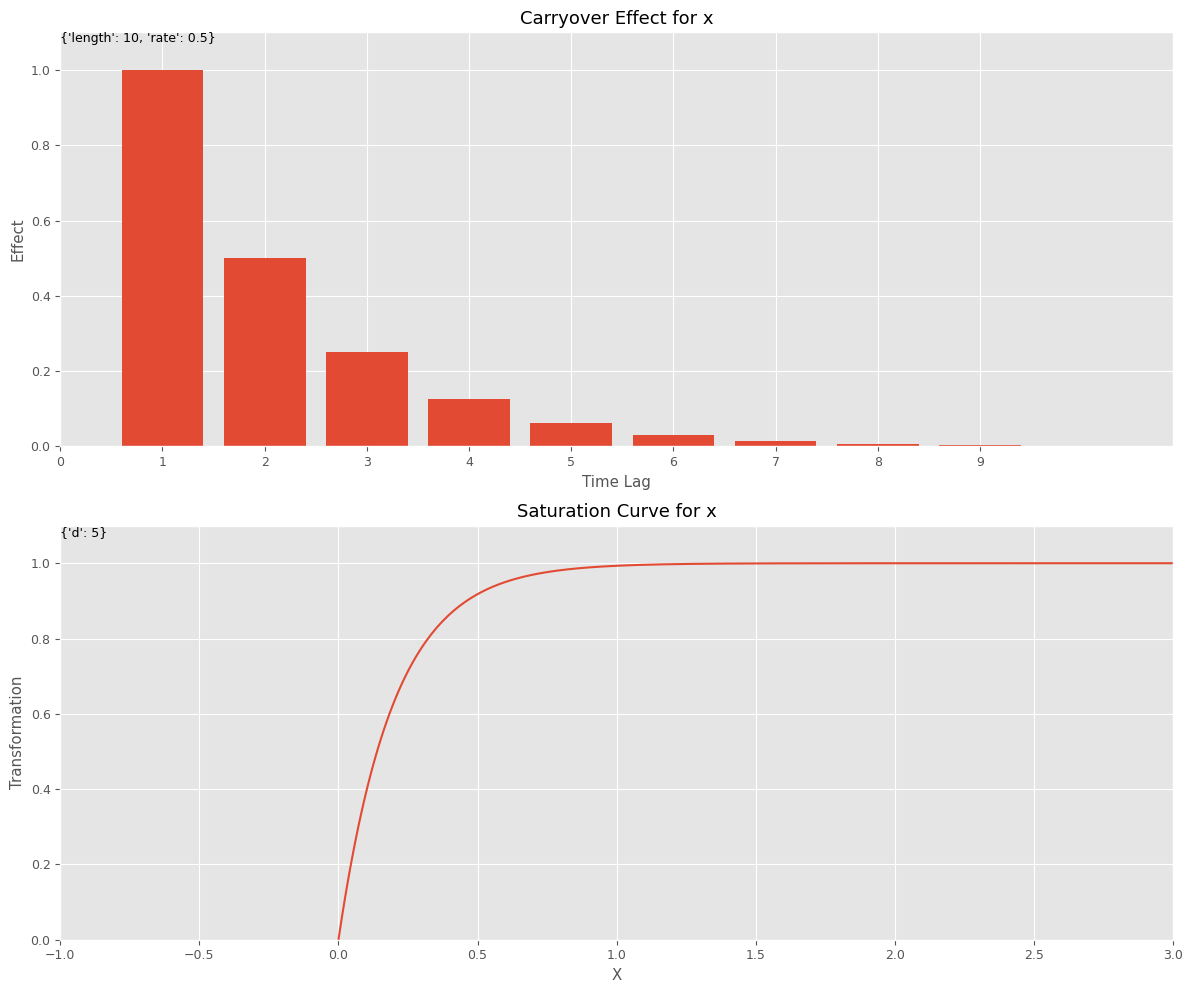
このようなシンプルなアドストックでも組み込むことで、構築されるMMMの精度が高くなります。

 

今回は、以下のようなピークが広告販促媒体によって変化するなど、やや一般的なアドストック（上がキャリオーバー効果関数、下が飽和関数）で、MMMを構築するお話しをします。

 

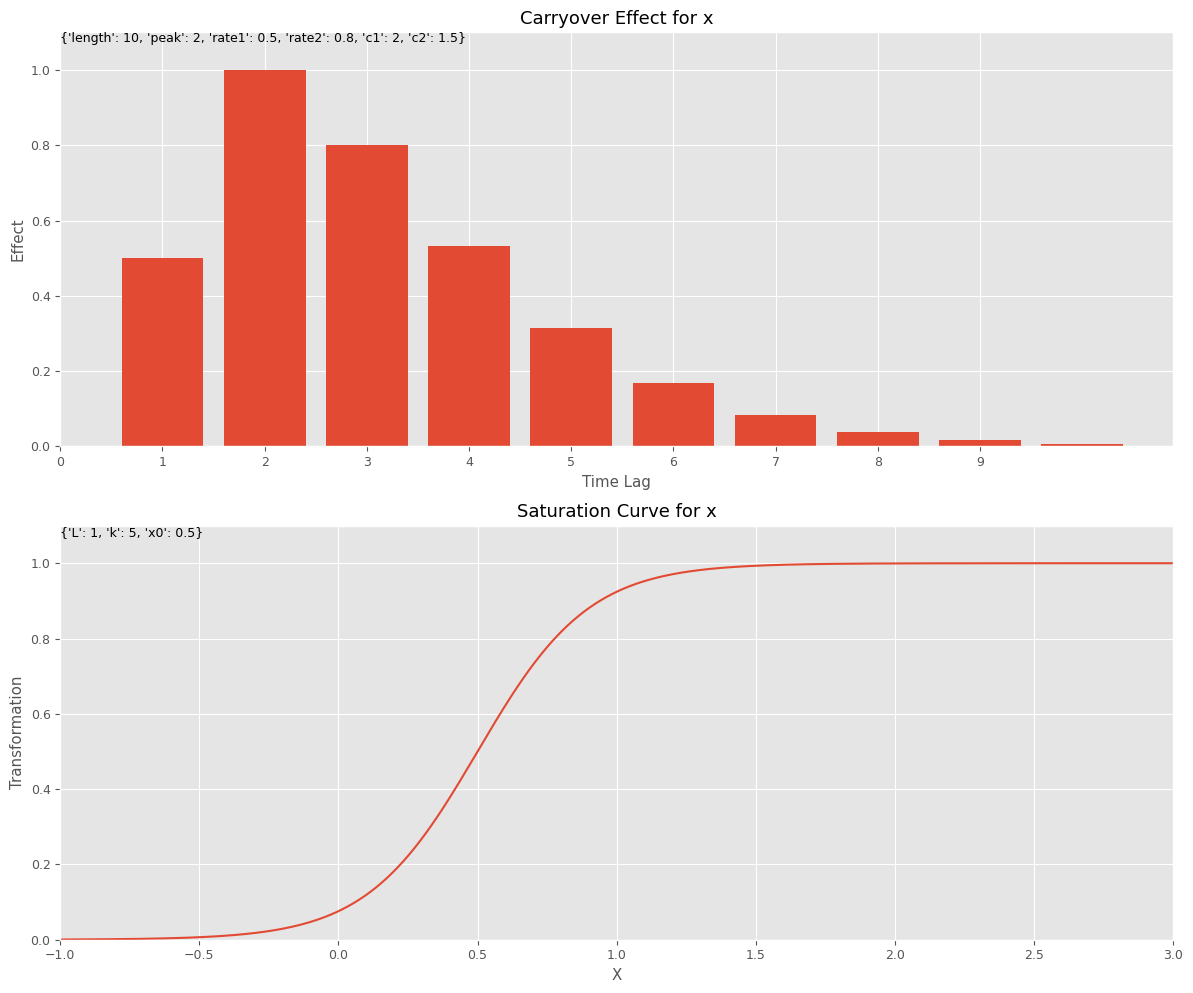
前回同様、推定器としてRidge回帰を利用します。

なぜならば、広告販促系のデータは、お互いの相関関係が強い傾向（同じ時期に集中し広告投下など）があり、多重共線性問題が起こる可能性が低くないからです。

MMMパイプラインとアドストック

　パイプラインの構造

MMMにアドストック（Ad Stock）を組み込むには、パイプラインを構築するといいでしょう。このようなパイプラインを、ここではMMMパイプラインと表現することにします。

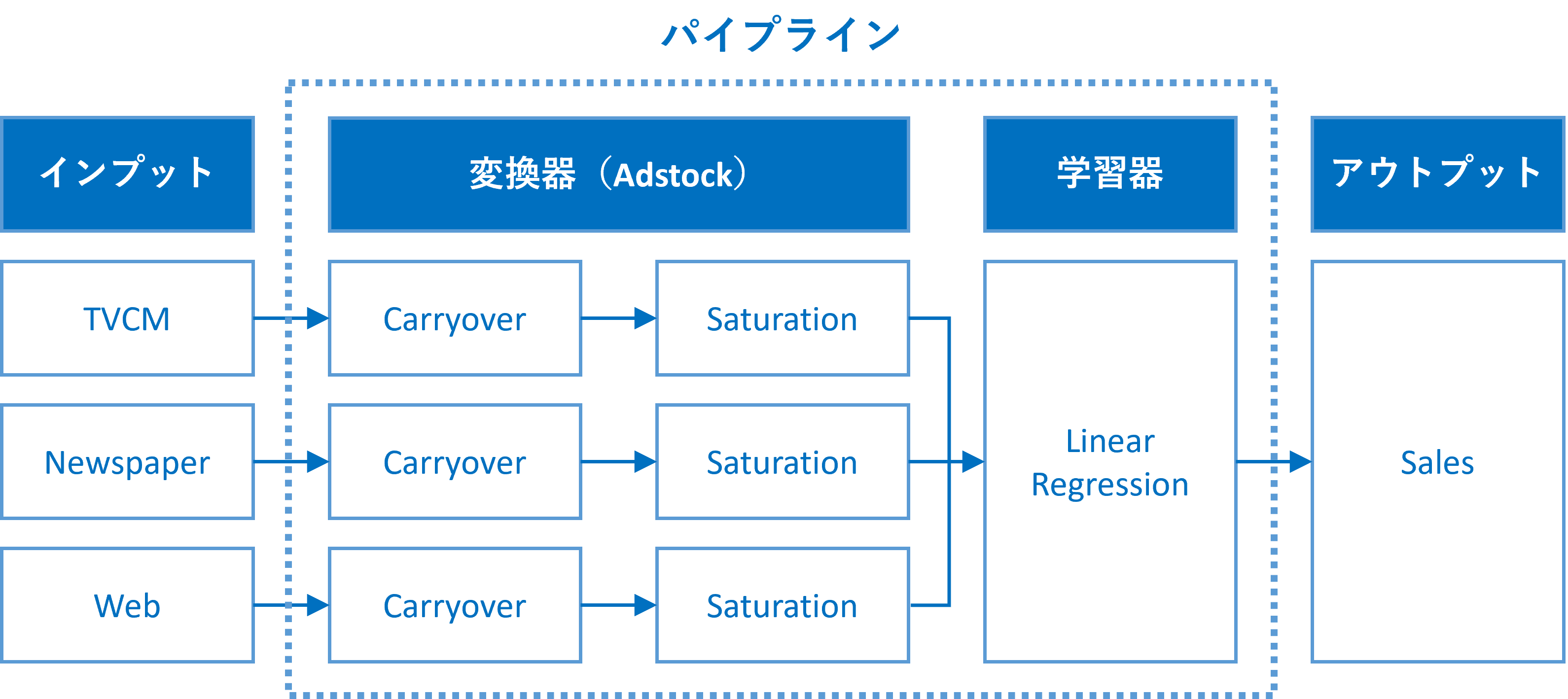
このMMMパイプラインは、少なくとも2つの変換器と1つの推定器が必要になります。

• 変換器
  • キャリーオーバー効果関数（Carryover）
  • 飽和関数（Saturation）
• 推定器
  • 線形回帰系のモデル（Linear Regression）：今回はRidge回帰を利用

 

各広告販促の投下量のデータごとに（要は、各変数ごとに）、その広告販促に応じた変換（キャリーオーバー効果関数→飽和関数）を施し、その変換結果を用い推定器である線形系のモデルを構築し、売上を表現するモデルを作り上げます。

 

　キャリーオーバー効果関数

広告販促などには通常、キャリーオーバー効果（Carryover）と呼ばれるものがあります。効果が後々まで残っているというものでラグ効果や残存効果とも言われます。

前回は、広告販促の投入時に最も効果が大きく、時間がたつにつれて徐々に薄れながらも残存して残っている、シンプルなキャリーオーバー効果を使いました。

 

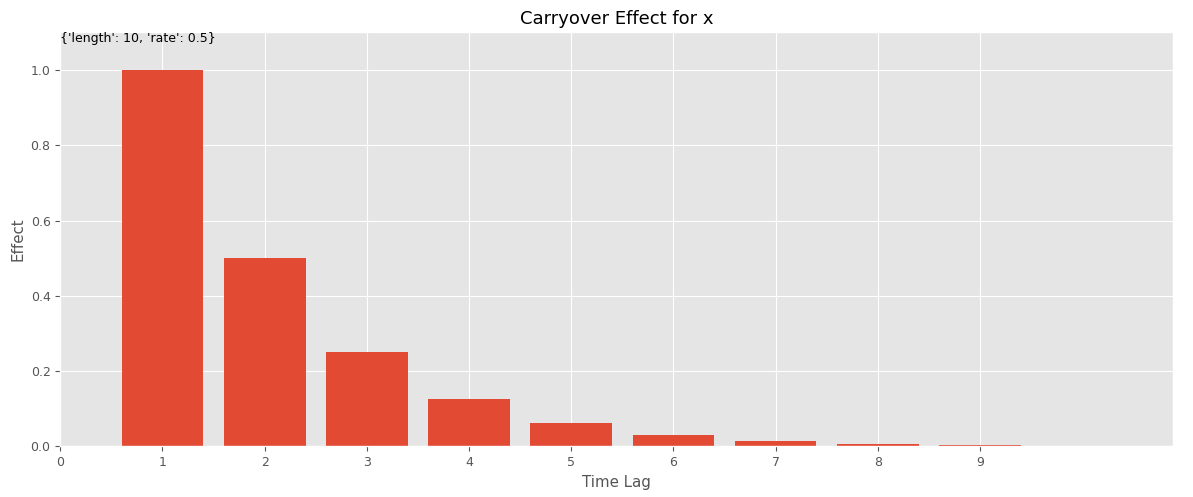
実際は、あらゆる広告や販促が、投下したときが効果のピークとは限りません。ちょっとずれることもあります。そのあたりを表現できると、より柔軟なキャリーオーバー効果関数になることでしょう。

今回は、以下のような、ピークが広告の投入時に限定するのではなく、媒体によって変化することを強要するキャリーオーバー効果関数を使います。

 

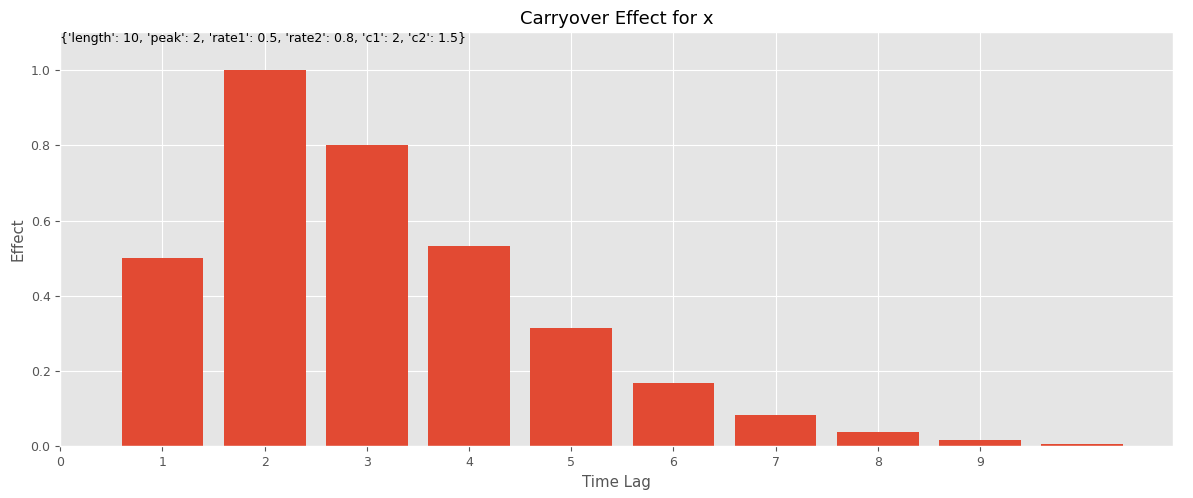
数式で表現すると、次のようになります。

ちょっと一般的なキャリーオーバー効果関数

\displaystyle x_t^* = \frac{\displaystyle \sum_{l=1}^{L} w_{t-l+1} \cdot x_{t-l+1}}{\displaystyle \sum_{l=1}^{L} w_{t-l+1}} , \quad w_{t-l+1} = \left\{ \begin{array}{cl} R_1^{|l-P|^{c_1}} & , \ l \leq P \\ R_2^{|l-P|^{c_2}} & , \ l > P \end{array} \right.

 

x_t は t 期の広告などの投入量で、x_t^* は t 期とそれ以前までの広告などの効果の累積（残存効果を足したもの）です。

このように、キャリーオーバー効果関数は、単にキャリーオーバーの現象をモデル化するだけでなく、それを足し合わせるような関数です。

\displaystyle x_t \overset{Carryover}{\Rightarrow} x_t^{*}

 

この関数には、以下の6つのハイパーパラメータがあります。

• L(length)：効果の続く期間（当期含む、そのため最小値は1）
• P(peak)：ピークの時期（広告などを打った日の場合は1、次期は2、など）
• R_1(rate1)：減衰率（ピーク時点より前）
• R_2(rate2)：減衰率（ピーク時点以降）
• c_1(c1)：減衰曲線の形状パラメータ（ピーク時点より前）
• c_1(c1)：減衰曲線の形状パラメータ（ピーク時点以降）

 

この効果の続く期間 L(length)とは、どのくらいまで考慮するか、ということです。

例えば、広告などを投下した期のみ効果がでるなら、L=1になります。7日間効果がでるなら、L=7になります。

 

このピークの時期 P(peak)とは、効果が最大となるピークの時期です。

例えば、広告などを投下した期がピークなら、P=1になります。2日間後にピークがくるなら、P=3になります。

 

2つの減衰率 R_1(rate1)とR_2(rate2)は、ピーク時期から離れているほど効果が減ることを表現したものです。c_1(c1)とc_2(c2)は、減衰曲線の形状を調整するパラメータです。

 

Pythonのコードでこの関数を表現すると以下のようになります。

# キャリオーバー効果関数
def carryover_advanced(X: np.ndarray, length, peak, rate1, rate2, c1, c2):
    X = np.append(np.zeros(length-1), X)
    
    Ws = np.zeros(length)
    
    for l in range(length):
        if l<peak-1:
            W = rate1**(abs(l-peak+1)**c1)
        else:
            W = rate2**(abs(l-peak+1)**c2)
        Ws[length-1-l] = W
    
    carryover_X = []
    
    for i in range(length-1, len(X)):
        X_array = X[i-length+1:i+1]
        Xi = sum(X_array * Ws)/sum(Ws)
        carryover_X.append(Xi)
        
    return np.array(carryover_X)

 

このコードは、キャリオーバー効果を計算するための関数carryover_advancedを定義しています。

• 入力データXの前にlength-1個のゼロを追加します。これは、計算開始時に十分なデータポイントを持つためです。
• lengthの長さを持つウェイト（重み）配列Wsをゼロで初期化します。
• ウェイト配列Wsを計算します。これは、各時点のキャリオーバー効果の強さを表します。ピーク時点より前はrate1とc1に基づいた減衰率で計算され、ピーク時点以降はrate2とc2に基づいて計算されます。
• キャリオーバー効果を考慮した時系列データcarryover_Xを計算します。これは、元のデータセットXをウェイト配列Wsで加重平均したものです。各時点でのキャリオーバー効果は、その時点を含むlength期間のデータに基づいて計算されます。
• 最終的に、計算されたキャリオーバー効果を含む時系列データcarryover_XをNumPy配列として返します。

 

この関数はパイプラインで利用するとき、クラスにして利用します。

以下、コードです。

# キャリオーバー効果を適用するカスタム変換器クラス
class CustomCarryOverTransformer(BaseEstimator, TransformerMixin):
    def __init__(self, carryover_params=None):
        self.carryover_params = carryover_params if carryover_params is not None else []

    def fit(self, X, y=None):
        return self

    def transform(self, X):
        if isinstance(X, pd.DataFrame):
            X = X.to_numpy()
        transformed_X = np.copy(X)
        for i, params in enumerate(self.carryover_params):
            transformed_X[:, i] = carryover_advanced(X[:, i], **params)
        return transformed_X

 

このコードは、キャリオーバー効果のカスタム変換器クラスCustomCarryOverTransformerを定義しています。

クラスの主要な部分は以下の通りです。

• __init__メソッド
  • このメソッドはクラスのコンストラクタ（クラスのインスタンス生成時に実行されるメソッド）です。
  • 引数carryover_paramsは、各特徴量に適用するキャリオーバー効果のパラメータを格納したリストです。
  • パラメータが指定されない場合、デフォルトで空のリストが割り当てられます。
• fitメソッド
  • このメソッドはX（特徴量）とy（目的変数）を引数として受け取り学習を実施します。
  • ただ、このメソッドは現在のインスタンスをそのまま返します。この変換器がfitによる学習をしないためです。
• transformメソッド
  • transformメソッドは、入力データXにキャリオーバー効果を適用し、変換されたデータを返します。
  • まず、入力XがpandasのDataFrameである場合、NumPy配列に変換されます。
  • 次に、Xの各特徴量（列）に対して、carryover_paramsに格納されたパラメータを使用してcarryover_advanced関数を適用します。
  • これにより、各特徴量は指定されたキャリオーバー効果に基づいて変換されます。変換プロセスは、各特徴量の列に対して個別に行われます。

このカスタム変換器クラスを使用することで、時系列データセット内の一つまたは複数の特徴量に対して、柔軟かつ効率的にキャリオーバー効果を適用することができます。キャリオーバー効果のパラメータ（例えば、効果の長さ、ピークの位置、減衰率など）は、モデルのパフォーマンスを最適化するために調整することが可能です。これは、特に広告支出の効果やその他の時間依存的な影響を分析する場合に有用です。

 

　飽和関数

広告販促の投下量を増やせば増やすほど売上などは上昇します。しかし、売上の上昇幅は鈍くなります。経済学でいうところの収穫逓減が起こります。

前回は、以下のような、ある時点を境に売上は飽和しいくら投下しても売上が伸びなくなる、最もシンプルな指数関数exp(*)で表現した飽和関数を利用しました。

 

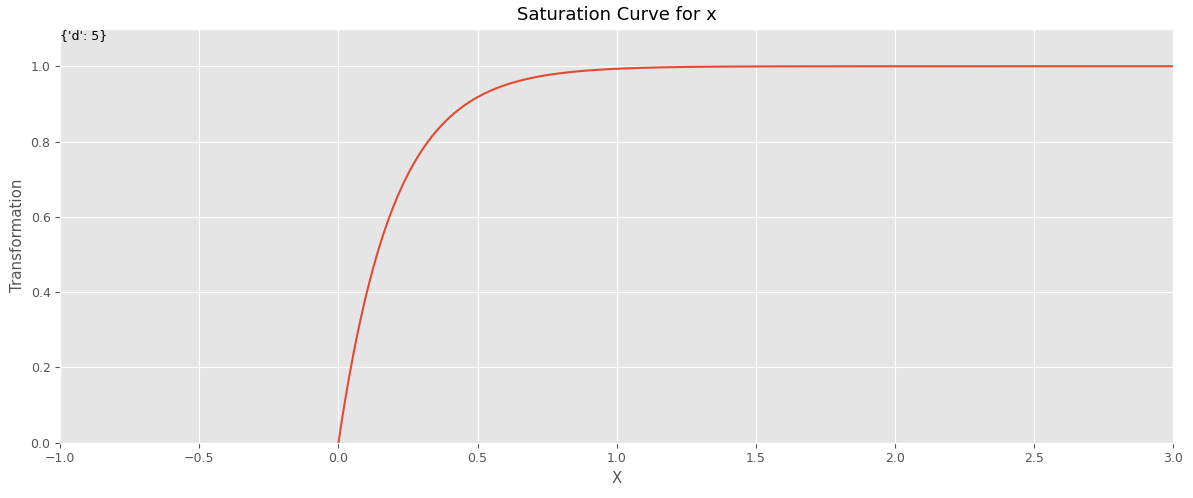
実際は、ある時点を境に売上は飽和しいくら投下しても売上が伸びなくなる、というだけではなく、効果がでるまでにある程度の投下量が必要になるケースが多いです。そうなると、S字曲線で表現できるほうがいいでしょう。

今回は、以下のような、S字曲線を表現するロジスティック曲線で表現した飽和関数を利用します。

 

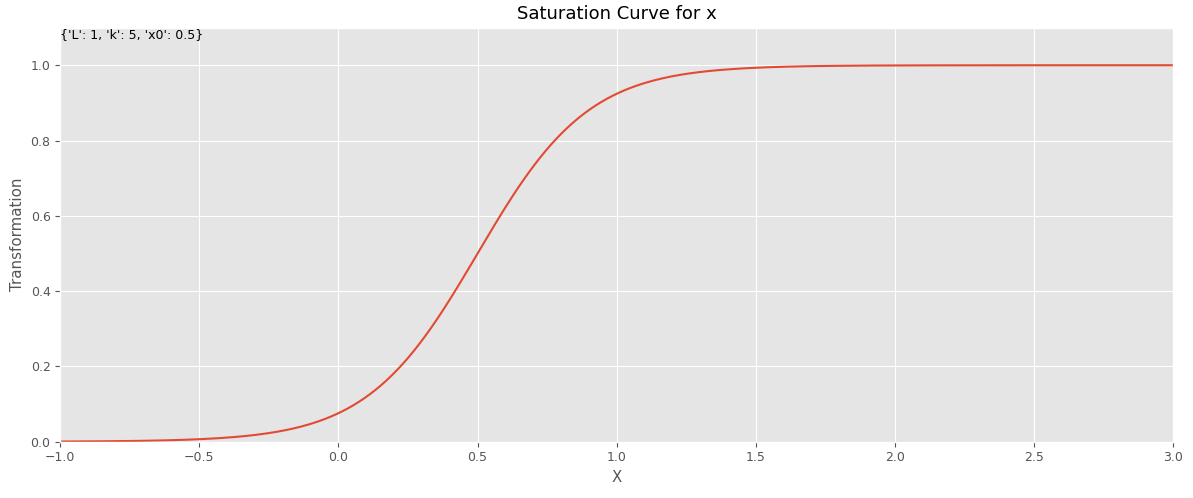
数式で表現すると、次のようになります。

飽和関数（ロジスティック型）

\displaystyle x_t^{**} = \frac{L}{1+e^{- k (x_t^*-x_0)}}

 

x_t^* は、 キャリーオーバー効果を考慮したt 期の広告などの説明変数（特徴量）の値です。つまり、キャリーオーバー効果関数で変換した後の説明変数（特徴量）の値です。x_t^{**} は、この x_t^* に対し 飽和効果を考慮した値（変換した値）です。

\displaystyle x_t \overset{Carryover}{\Rightarrow} x_t^{*} \overset{Saturation}{\Rightarrow} x_t^{**}

このx_t^{**} を利用し、推定器（今回はRidge回帰）のインプットとして利用します。

 

この関数のハイパーパラメータは、次の3つです。

• L ：上限パラメータ（曲線の最大値）
• k ：形状パラメータ（大きいほど、曲線はより急なS字形になります）
• x_0 ：位置パラメータ（曲線が最も急に成長する点）

 

Pythonのコードでこの関数を表現すると以下のようになります。

# 飽和関数（ロジスティック曲線）
def logistic_function(x, L, k, x0):
    result = L / (1+ np.exp(-k*(x-x0)))  
    return result

 

このコードは、飽和関数logistic_functionを定義しています。

• L / (1 + np.exp(-k*(x-x0)))は、xが増加するにつれて0からLに向かって漸近的に増加する値を計算します。
• np.exp(-k*(x-x0))は指数関数です。xがx0から離れるにつれて、この値は急速に増加または減少し、曲線の形状を決定します。

この関数は、入力xに対してロジスティック関数の値を計算し、その結果を返します。

 

この関数はパイプラインで利用するとき、クラスにして利用します。

以下、コードです。

# 飽和関数を適用するカスタム変換器クラス
class CustomSaturationTransformer(BaseEstimator, TransformerMixin):
    def __init__(self, curve_params=None):
        self.curve_params = curve_params if curve_params is not None else []
    def fit(self, X, y=None):
        return self
    def transform(self, X):
        if isinstance(X, pd.DataFrame):
            X = X.to_numpy()
        transformed_X = np.copy(X)
        for i, params in enumerate(self.curve_params):
            transformed_X[:, i] = logistic_function(X[:, i], **params)
        return transformed_X

 

このコードは、ロジスティック関数（飽和関数）をデータセットの特定の特徴量に適用するためのカスタム変換器クラスCustomSaturationTransformerを定義しています。

• __init__メソッド
  • クラスのコンストラクタです。
  • 引数curve_paramsは、ロジスティック関数を適用する際に使用するパラメータ（L、k、x0）のリストです。
  • パラメータが提供されない場合、デフォルトで空のリストが使用されます。
• fitメソッド
  • 現在のインスタンスをそのまま返します。
  • この変換器がfitによる学習をしないためです。
• transformメソッド
  • 入力XがpandasのDataFrameである場合、まずNumPy配列に変換されます。
  • その後、各特徴量（列）に対して、curve_paramsで指定されたロジスティック関数のパラメータを使用してlogistic_function関数を適用します。
  • これにより、元の特徴量は指定された飽和曲線に基づいて変換されます。

このカスタム変換器クラスを使用することで、データセット内の特徴量に非線形変換（ロジスティック曲線による変換）を適用します。

 

利用するデータセット

前回同様、以下のデータセットを前提に説明します。

• 目的変数：売上金額（Sales）
• 説明変数：TVCM、Newspaper、Webのコスト

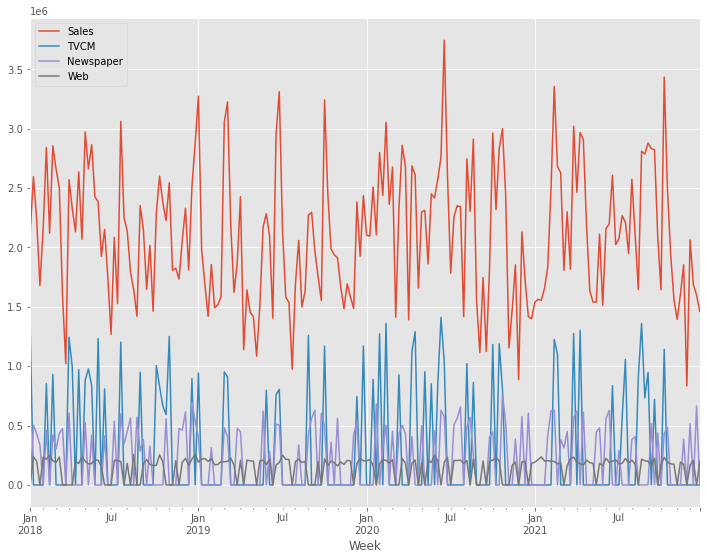
今回利用するデータセットは、以下からダウンロードできます。

MMM.csv
https://www.salesanalytics.co.jp/4zdt

 

目的変数は、売上金額である必要はありません。例えば、売上点数でも受注件数、問い合せ件数、予約件数でも構いません。要は、広告販促でより良い変化をさせたい何かです。

説明変数は、コストでなくても構いません。例えば、媒体の認知や接触、露出、広告のクリック、インプレッション、配信、開封などでも構いません。ただ、コスパという概念を持ち出すとき、少なくともコストデータは必要になります。

 

準備

今回利用するモジュールやデータセットの読み込み、先ほど述べたアドストック系関数の定義などを実施していきます。

 

　モジュールなどの読み込み

　　共通利用するモジュール

以下、コードです。

import numpy as np
import pandas as pd
import optuna

from sklearn.linear_model import Ridge

from sklearn.base import BaseEstimator, TransformerMixin
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import MinMaxScaler
from sklearn.model_selection import TimeSeriesSplit
from sklearn.model_selection import cross_val_score

from functools import partial

import warnings
warnings.simplefilter('ignore')

import matplotlib.pyplot as plt
plt.style.use('ggplot') #グラフスタイル
plt.rcParams['figure.figsize'] = [12, 7] #グラフサイズ
plt.rcParams['font.size'] = 9 #フォントサイズ

 

簡単に説明します。

• import numpy as np
  • NumPyは、数値計算を効率的に行うための基本的なライブラリ。
• import pandas as pd
  • Pandasは、データ構造とデータ分析ツールを提供するライブラリ。
• import optuna
  • Optunaは、機械学習モデルのハイパーパラメータを最適化するためのライブラリ。
• from sklearn.linear_model import Ridge
  • scikit-learnは機械学習のためのライブラリで、ここでは線形モデルの一つであるリッジ回帰（Ridge）をインポート。
• from sklearn.base import BaseEstimator, TransformerMixin
  • scikit-learnの基本クラスであるBaseEstimatorと、変換器のためのミックスインクラスであるTransformerMixin。
  • クラスを作るときに利用。
• from sklearn.pipeline import Pipeline
  • データ処理とモデルの構築を一連のステップとして管理するためのパイプライン機能。
• from sklearn.preprocessing import MinMaxScaler
  • MinMaxScalerはデータの正規化を行うためのツール。
  • 最小値が0、最大値が1になりように正規化。
• from sklearn.model_selection import TimeSeriesSplit
  • TimeSeriesSplitは時系列クロスバリデーションで利用。
• from sklearn.model_selection import cross_val_score
  • モデルの評価を行うためのcross_val_score関数をインポート。
• from functools import partial
  • 関数に事前に引数を設定するためのpartialをインポート。
• import warnings
  • Pythonの警告制御ツールをインポート。
  • warnings.simplefilter('ignore')
    • 警告を無視するように設定。
• import matplotlib.pyplot as plt
  • データの可視化を行うためのライブラリであるMatplotlibをインポートします。
  • plt.style.use('ggplot')
    • グラフのスタイルをggplot風に設定。
  • plt.rcParams['figure.figsize'] = [12, 7]
    • グラフのデフォルトサイズを設定。
  • plt.rcParams['font.size'] = 9
    • グラフのフォントサイズを設定。

 

　　前々回作った関数群（MMM構築・評価など）

さらに今回は、前々回作った以下の関数群を使います。

• MMM構築
  • train_and_evaluate_model:MMMの構築
  • plot_actual_vs_predicted:構築したMMMの予測値の時系列推移
• 後処理（結果の出力）
  • calculate_and_plot_contribution:売上貢献度の算出（時系列推移）
  • summarize_and_plot_contribution:売上貢献度構成比の算出
  • calculate_marketing_roi:マーケティングROIの算出

 

以下からダウンロードできます。

mmm_functions.py　※zipファイルを解凍してお使いください
https://www.salesanalytics.co.jp/oi17

 

興味のある方、詳細を知りたい方は、以下を参照ください。

PythonによるMMM（マーケティングミックスモデリング）とビジネス活用－ 振返り分析編（その2）：線形回帰系モデルでのMMM構築 －

 

mmm_functions.pyを利用するときは、実行するPythonファイルやNotebookと同じフォルダに入れておいてください。

以下のコードで呼び出せます。

from mmm_functions import *

 

上手くいかないときは、mmm_functions.pyをメモ帳などで開き内容をコピーし、実行するPythonファイルやNotebookにコードを張り付け、Pythonで関数を作ってからMMM構築などを行ってください。

 

　データセットの読み込み

以下、コードです。

# データセット読み込み
dataset = 'https://www.salesanalytics.co.jp/4zdt'
df = pd.read_csv(
    dataset,
    parse_dates=['Week'],
    index_col='Week',
)

# 説明変数Xと目的変数yに分解
X = df.drop(columns=['Sales'])
y = df['Sales']

 

• データセット読み込み:
  • dataset = 'https://www.salesanalytics.co.jp/4zdt': ここで、データセットのURLが指定されています。
  • df = pd.read_csv(...): この行では、Pandasライブラリのread_csv関数を使用して、指定されたURLからデータセットを読み込んでいます。この関数は、CSV形式（カンマ区切りの値）のデータを読み込むのに広く使われています。
    • parse_dates=['Week']: この引数は、’Week’列を日付型のデータとして解析するように指示しています。
    • index_col='Week': この引数は、’Week’列をデータフレームのインデックス（行のラベル）として使用するように指示しています。
• 説明変数Xと目的変数yに分解:
  • X = df.drop(columns=['Sales']): ここでは、dropメソッドを使用して’Sales’列を除外し、残りの列を説明変数Xとして保持しています。dropは指定された列をデータフレームから削除するために使われます。
  • y = df['Sales']: この行では、’Sales’列を目的変数yとして抽出しています。目的変数は、モデルによって予測されるべき変数であり、このケースでは売上データと思われます。

 

目的変数y（売上）をプロットします。

以下、コードです。

y.plot()
plt.show()

 

以下、実行結果です。

 

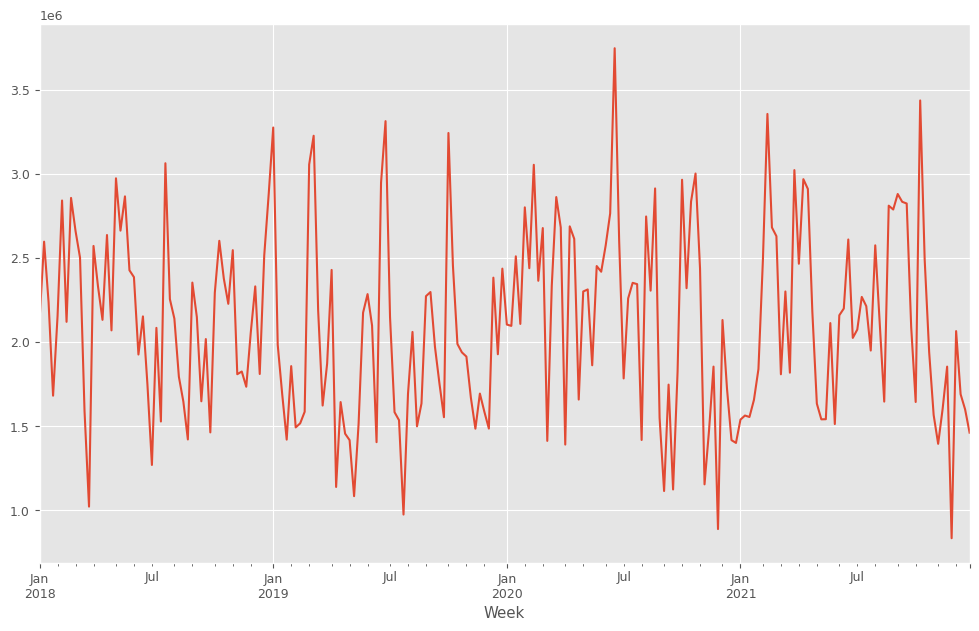
• y.plot(): y（目的変数）を折れ線グラフで表示します。plot()はPandasのデフォルトのグラフ化するためのプロット機能です。
• plt.show(): 作成されたグラフを画面に出力します。

 

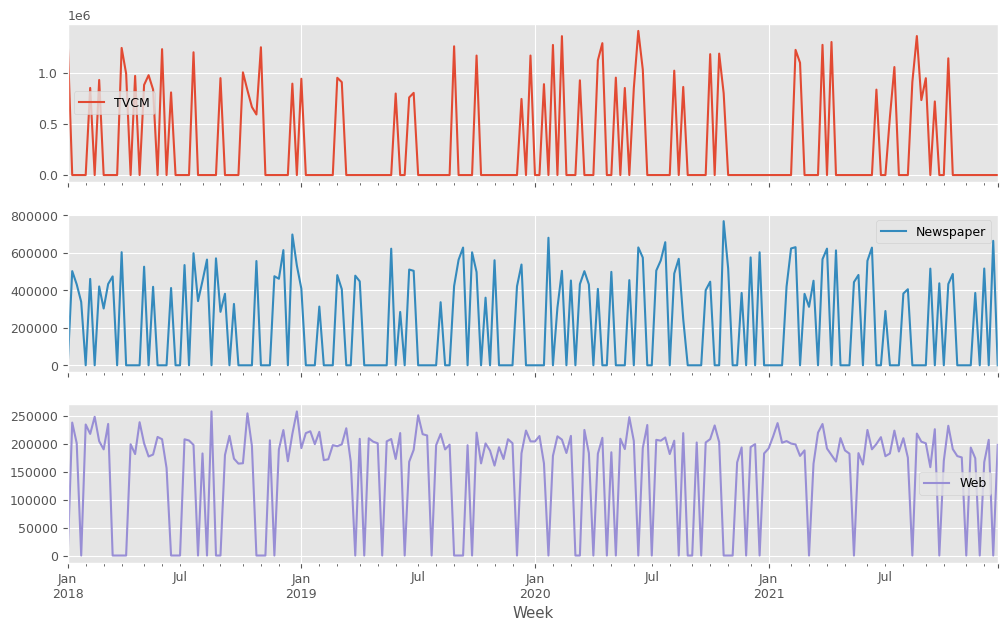
説明変数X（各メディアのコスト）をまとめてプロットします。

以下、コードです。

X.plot(subplots=True)
plt.show()

 

• X.plot(subplots=True): X（説明変数）を折れ線グラフで表示します。subplots=Trueは、Xの各列（各媒体）を別々のサブプロットとして表示することを意味します。これにより、各説明変数の動きを個別に確認できます。
• plt.show(): 作成されたグラフを画面に出力します。

 

以下、実行結果です。

 

　アドストック系の関数とクラス、そのグラフ化関数の定義

先ほどと重複しますが、アドストック系の関数である、シンプルなキャリーオーバー効果関数とそのクラス、シンプルな飽和関数とそのクラス、そしてそれらを視覚化（グラフ）する関数を作っていきます。

 

　　キャリオーバー効果関数

先ずは、シンプルなキャリーオーバー効果関数とそのクラスを作ります。

以下、コードです。

# キャリオーバー効果関数
def carryover_advanced(X: np.ndarray, length, peak, rate1, rate2, c1, c2):
    X = np.append(np.zeros(length-1), X)
    
    Ws = np.zeros(length)
    
    for l in range(length):
        if l<peak-1:
            W = rate1**(abs(l-peak+1)**c1)
        else:
            W = rate2**(abs(l-peak+1)**c2)
        Ws[length-1-l] = W
    
    carryover_X = []
    
    for i in range(length-1, len(X)):
        X_array = X[i-length+1:i+1]
        Xi = sum(X_array * Ws)/sum(Ws)
        carryover_X.append(Xi)
        
    return np.array(carryover_X)

# キャリオーバー効果を適用するカスタム変換器クラス
class CustomCarryOverTransformer(BaseEstimator, TransformerMixin):
    def __init__(self, carryover_params=None):
        self.carryover_params = carryover_params if carryover_params is not None else []

    def fit(self, X, y=None):
        return self

    def transform(self, X):
        if isinstance(X, pd.DataFrame):
            X = X.to_numpy()
        transformed_X = np.copy(X)
        for i, params in enumerate(self.carryover_params):
            transformed_X[:, i] = carryover_advanced(X[:, i], **params)
        return transformed_X

 

　　飽和関数

次に、シンプルな飽和関数とそのクラスを作ります。

以下、コードです。

# 飽和関数（ロジスティック曲線）
def logistic_function(x, L, k, x0):
    result = L / (1+ np.exp(-k*(x-x0)))  
    return result

# 飽和関数を適用するカスタム変換器クラス
class CustomSaturationTransformer(BaseEstimator, TransformerMixin):
    def __init__(self, curve_params=None):
        self.curve_params = curve_params if curve_params is not None else []
    def fit(self, X, y=None):
        return self
    def transform(self, X):
        if isinstance(X, pd.DataFrame):
            X = X.to_numpy()
        transformed_X = np.copy(X)
        for i, params in enumerate(self.curve_params):
            transformed_X[:, i] = logistic_function(X[:, i], **params)
        return transformed_X

 

　　アドストック視覚化（グラフ）関数

どのようなアドストックになっているのかを視覚的に理解するために、視覚化（グラフ）する関数を作ります。

以下、コードです。

def plot_carryover_effect(params, feature_name, fig, axes, i):
    max_length = max(10, params['length'])
    x = np.concatenate(([1], np.zeros(max_length - 1)))
    y = carryover_advanced(x, **params)
    y = y / max(y)
    axes[2*i].bar(np.arange(1, max_length + 1), y)
    axes[2*i].set_title(f'Carryover Effect for {feature_name}')
    axes[2*i].text(0, 1.1, params, ha='left',va='top')
    axes[2*i].set_xlabel('Time Lag')
    axes[2*i].set_ylabel('Effect')
    axes[2*i].set_xticks(range(len(y)))
    axes[2*i].set_ylim(0, 1.1)

def plot_saturation_curve(params, feature_name, fig, axes, i):
    x = np.linspace(-1, 3, 400)
    y = logistic_function(x, **params) 
    axes[2*i+1].plot(x, y, label=feature_name)
    axes[2*i+1].set_title(f'Saturation Curve for {feature_name}')
    axes[2*i+1].text(-1, max(y)* 1.1, params, ha='left',va='top')
    axes[2*i+1].set_xlabel('X')
    axes[2*i+1].set_ylabel('Transformation')
    axes[2*i+1].set_ylim(0, max(y) * 1.1)
    axes[2*i+1].set_xlim(-1, 3)

def plot_effects(carryover_params, curve_params, feature_names):
    fig, axes = plt.subplots(len(feature_names) * 2, 1, figsize=(12, 10*len(feature_names)))
    for i, params in enumerate(carryover_params):
        plot_carryover_effect(params, feature_names[i], fig, axes, i)
    for i, params in enumerate(curve_params):
        plot_saturation_curve(params, feature_names[i], fig, axes, i)
    plt.tight_layout()
    plt.show()

 

このコードは、キャリオーバー効果と飽和曲線をプロットするための関数plot_effectsを定義しています。広告や販促などの効果が時間の経過によってどのように変化するか（キャリオーバー効果）、また、ある入力に対する反応が一定のポイントを超えると増加が鈍化する（飽和）様子を視覚化するのに使用します。

大きく、キャリーオーバー効果のプロット部分と、飽和曲線のプロットの部分に分かれます。

このコードは、特定の特徴量に対するキャリーオーバー効果と飽和曲線を可視化するためのものです。

キャリーオーバー効果関数をグラフ化するplot_carryover_effect 関数と、飽和関数をグラフ化するplot_saturation_curve 関数、この2つの関数を統合しプロットするplot_effects 関数で構成されています。

簡単に説明します。

• plot_carryover_effect関数
  • この関数は、指定された特徴量に対するキャリオーバー効果を可視化します。
  •  以下は関数の引数：
    • params: キャリオーバー効果を計算するためのパラメータが格納された辞書。
    • feature_name: 可視化する特徴量の名前。
    • fig: matplotlibのfigureオブジェクト。
    • axes: グラフを描画するためのaxesオブジェクトの配列。
    • i: 特徴量のインデックス。これは、対応する軸を識別するために使用されます。
  • この関数は、キャリオーバー効果の強度を時間遅延に対してプロットします。効果の強度は正規化されており、最大値が1になるように調整されています。
  • プロットは棒グラフで表され、時間遅延ごとの効果の大きさを示しています。
• plot_saturation_curve関数
  • この関数は、特定の特徴量に対する飽和曲線をプロットします。
  •  以下は関数の引数：
    • params: ロジスティック関数のパラメータが格納された辞書。
    • feature_name: 可視化する特徴量の名前。
    • fig: matplotlibのfigureオブジェクト。
    • axes: グラフを描画するためのaxesオブジェクトの配列。
    • i: 特徴量のインデックス。
  • この関数は、ロジスティック関数に基づいて飽和曲線を描画します。
  • xの範囲は-1から3までとされており、曲線の形状を詳細に観察できるようにしています。
• plot_effects関数
  • この関数は、特徴量に対するキャリオーバー効果と飽和曲線をまとめて可視化します。
  •  以下は関数の引数：
    • carryover_params: 各特徴量に適用するキャリオーバー効果のパラメータのリスト。
    • curve_params: 各特徴量に適用する飽和曲線のパラメータのリスト。
    • feature_names: 可視化する特徴量の名前のリスト。
  • plot_effects関数は、各特徴量に対してplot_carryover_effect関数とplot_saturation_curve関数を順に呼び出し、それぞれの効果を可視化します。
  • これにより、特徴量ごとにキャリオーバー効果と飽和曲線を並べて比較することが可能になります。
  • 最後に、plt.tight_layout()を使用してグラフ間の配置を調整し、plt.show()でグラフを表示します。

 

この関数を利用してみます。

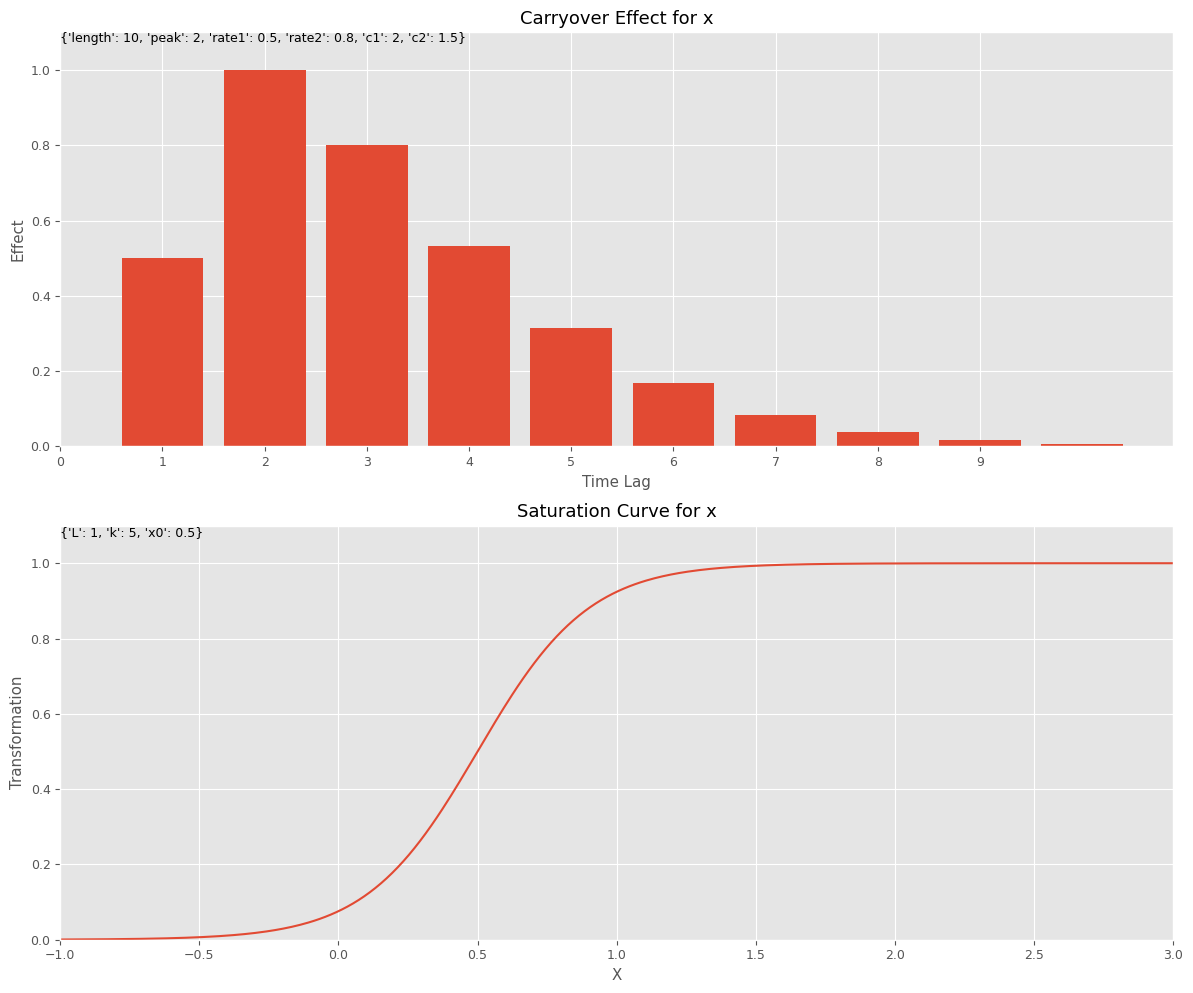
先ず、キャリーオーバー効果関数と飽和関数のハイパーパラメータを設定します。このハイパーパラメータを、今作った視覚化（グラフ）する関数にインプットしグラフを描きます。特徴量名は何を設定しても問題ございません。

以下、コードです。

# キャリーオーバー効果関数のハイパーパラメータの設定
carryover_params = [
    {'length': 10, 'peak': 2, 'rate1': 0.5, 'rate2': 0.8, 'c1': 2, 'c2': 1.5},
]

# 飽和関数のハイパーパラメータの設定
curve_params = [
    {'L': 1, 'k': 5, 'x0': 0.5},
]

# 特徴量名の設定
feature_names = ['x']

# グラフで確認
plot_effects(carryover_params, curve_params, feature_names)

 

以下、実行結果です。

 

MMMパイプライン構築（ハイパーパラメータ手動調整）

では、MMMパイプラインを構築していきます。

 

　ハイパーパラメータの設定

アドストック（キャリーオーバー効果関数と飽和関数）とRidge回帰にハイパーパラメータがあります。あらかじめ設定します。

以下、コードです。

# 各特徴量に対するキャリーオーバー効果のパラメータ設定
carryover_params = [
    {'length': 7, 'peak': 2, 'rate1': 0.7, 'rate2': 0.5, 'c1': 1, 'c2': 0.5},
    {'length': 3, 'peak': 1, 'rate1': 0.8, 'rate2': 0.3, 'c1': 0.5, 'c2': 1},
    {'length': 2, 'peak': 1, 'rate1': 1, 'rate2': 0.1, 'c1': 1, 'c2': 1},
]

# 各特徴量に対する飽和関数のパラメータ設定
curve_params = [
    {'L': 1, 'k': 10, 'x0': 0.5},
    {'L': 5, 'k': 10, 'x0': 0.5},
    {'L': 1, 'k': 10, 'x0': 0.7}
]

# 特徴量名の設定
feature_names = X.columns

# グラフで確認
plot_effects(carryover_params, curve_params, feature_names)

 

以下、実行結果です。

 

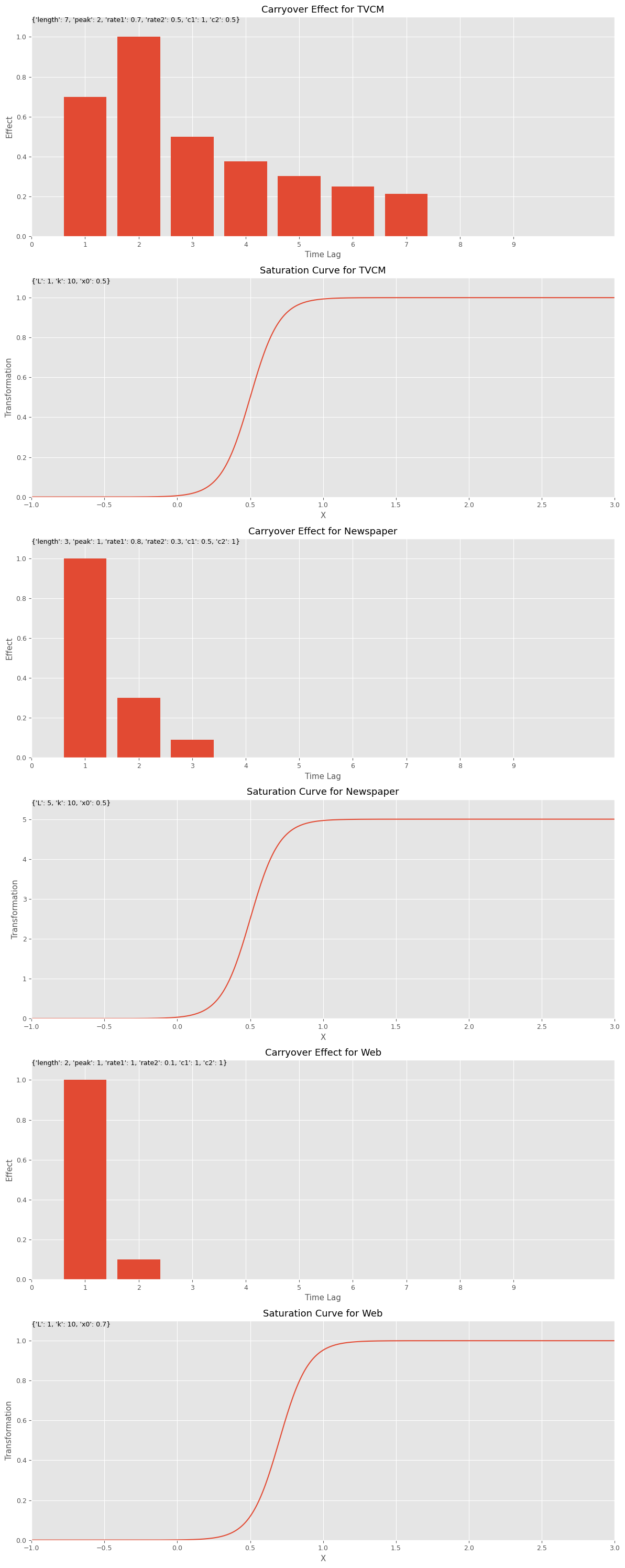
　MMM構築

この設定でMMMパイプラインを構築していきます。

以下、コードです。

# パイプラインの構築
MMM_pipeline = Pipeline([
    ('scaler', MinMaxScaler()),
    ('carryover_transformer', CustomCarryOverTransformer(carryover_params=carryover_params)),
    ('saturation_transformer', CustomSaturationTransformer(curve_params=curve_params)),
    ('ridge', Ridge(alpha=1))
])

# パイプラインを表示
print(MMM_pipeline)

 

このコードは、Scikit-LearnのPipelineクラスを用い、複数の変換処理（キャリーオーバー効果関数→飽和関数）と最終的な予測モデル（Ridge回帰）を一連のステップとして組み込んだMMMパイプラインを構築するものです。

パイプラインの各ステップを簡単に説明します。

• MinMaxScaler:
  • このステップでは、MinMaxScalerを使用して特徴量のスケーリングを行います。
  • これは、すべての特徴量を0と1の間に正規化することによって、異なるスケールの特徴量間のバランスを取り、モデルの性能を向上させるのに役立ちます。
• CustomCarryOverTransformer:
  • カスタム変換器CustomCarryOverTransformerを使用して、特定の特徴量に対するキャリオーバー効果をデータに適用します。
  • このステップでは、carryover_paramsに基づいて各特徴量に対してキャリオーバー効果が計算されます。
• CustomSaturationTransformer:
  • カスタム変換器CustomSaturationTransformerを使用して、データに飽和効果を適用します。
  • curve_paramsに基づいて各特徴量に対する飽和曲線が適用されます。
• Ridge:
  • 最終的なステップとして、リッジ回帰モデル（Ridge）が使用されます。
  • リッジ回帰は線形回帰の一種で、重みの大きさにペナルティを課す（L2正則化）ことでモデルの過学習を防ぎます。
  • alpha=1は正則化の強さを制御します。

 

以下、実行結果です。

Pipeline(steps=[('scaler', MinMaxScaler()),
                ('carryover_transformer',
                 CustomCarryOverTransformer(carryover_params=[{'c1': 1,
                                                               'c2': 0.5,
                                                               'length': 7,
                                                               'peak': 2,
                                                               'rate1': 0.7,
                                                               'rate2': 0.5},
                                                              {'c1': 0.5,
                                                               'c2': 1,
                                                               'length': 3,
                                                               'peak': 1,
                                                               'rate1': 0.8,
                                                               'rate2': 0.3},
                                                              {'c1': 1, 'c2': 1,
                                                               'length': 2,
                                                               'peak': 1,
                                                               'rate1': 1,
                                                               'rate2': 0.1}])),
                ('saturation_transformer',
                 CustomSaturationTransformer(curve_params=[{'L': 1, 'k': 10,
                                                            'x0': 0.5},
                                                           {'L': 5, 'k': 10,
                                                            'x0': 0.5},
                                                           {'L': 1, 'k': 10,
                                                            'x0': 0.7}])),
                ('ridge', Ridge(alpha=1))])

 

このMMMパイプラインを学習し、実測と予測の散布図を描いてみます。

以下、コードです。

# パイプラインを使って学習
MMM_pipeline.fit(X, y)

# 学習したモデルを使って予測
predictions = MMM_pipeline.predict(X)

# 予測結果の表示
plt.figure(figsize=(10, 6))
plt.scatter(y, predictions)
plt.plot([y.min(), y.max()], [y.min(), y.max()], 'k--', lw=3)
plt.xlabel('actual')
plt.ylabel('predicted')
plt.title('Actual vs Predicted Values')
plt.show()

 

このコードは、MMMパイプラインを学習（MMM_pipeline.fit(X, y)）し予測（predictions = MMM_pipeline.predict(X)）を行った後、実際の値（y）と予測値（predictions）を比較するためのグラフを描画しています。目的は、モデルの予測精度を視覚的に評価することです。

 

以下、実行結果です。

 

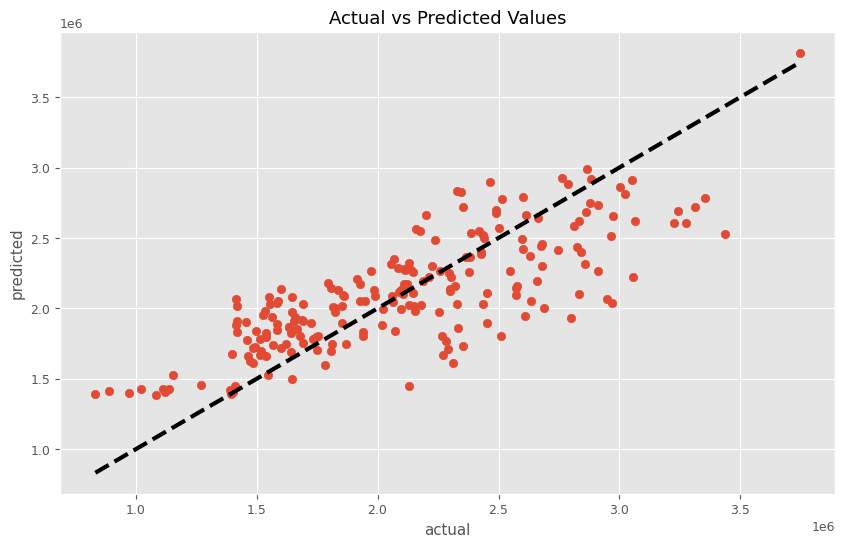
前々回作った以下の関数群を使い、MMMモデル構築から貢献度算出、マーケティングROIの計算をしていきます。

• MMM構築
  • train_and_evaluate_model:MMMの構築
  • plot_actual_vs_predicted:構築したMMMの予測値の時系列推移
• 後処理（結果の出力）
  • calculate_and_plot_contribution:売上貢献度の算出（時系列推移）
  • summarize_and_plot_contribution:売上貢献度構成比の算出
  • calculate_marketing_roi:マーケティングROIの算出

 

繰り返しの説明になります。

以下からダウンロードできます。

mmm_functions.py　※zipファイルを解凍してお使いください
https://www.salesanalytics.co.jp/oi17

 

mmm_functions.pyを利用するときは、実行するPythonファイルやNotebookと同じフォルダに入れておいてください。

以下のコードで呼び出せます。

from mmm_functions import *

 

上手くいかないときは、mmm_functions.pyをメモ帳などで開き内容をコピーし、実行するPythonファイルやNotebookにコードを張り付け、Pythonで関数を作ってからMMM構築などを行ってください。

 

関数train_and_evaluate_modelを使い、MMMを構築します。

以下、コードです。

# MMMの構築
trained_model, pred = train_and_evaluate_model(MMM_pipeline, X, y)

 

以下、実行結果です。

RMSE: 344075.4292652078
MAE: 275210.9825168048
MAPE: 0.138659898257034
R2: 0.620215473526532

 

ちなみに、以下は前回（シンプルなアドストックを考慮したMMM）の結果です。

RMSE: 175244.63286004536
MAE: 141136.68030802492
MAPE: 0.07014970643405759
R2: 0.9014811355562776

 

いい加減にアドストックを設定すると、結果は悪化するようです。

とは言え、結果を見ていきます。

 

関数plot_actual_vs_predictedを使い、関数train_and_evaluate_modelで構築したMMMの予測値と実測値をプロットします。

以下、コードです。

# 実測値と予測値の時系列推移
plot_actual_vs_predicted(y.index, y.values, pred.y.values, (0, 4e6))

 

以下、実行結果です。

 

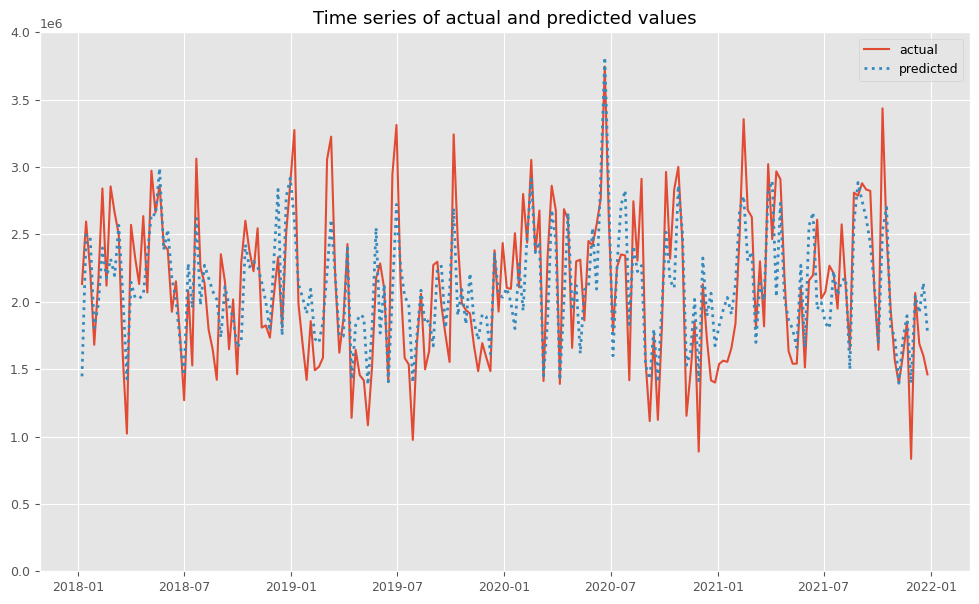
　後処理（結果の出力）

MMMを構築したら、貢献度やマーケティングROIなどを計算していきます。

先ずは、貢献度を計算します。

以下、コードです。

# 貢献度の算出
contribution = calculate_and_plot_contribution(y, X, trained_model,(0, 4e6))

 

以下、実行結果です。

                    Base           TVCM      Newspaper            Web
Week                                                                 
2018-01-07  2.039240e+06   92760.432443       0.000000       0.000000
2018-01-14  1.439387e+06  155990.999485  395597.019160  605125.127001
2018-01-21  1.245492e+06   28999.779417  493163.999397  468544.304804
2018-01-28  1.287747e+06   18413.004212  374104.412924     635.352780
2018-02-04  1.505418e+06   15380.750414   17503.158557  617097.629782
...                  ...            ...            ...            ...
2021-11-28  8.266129e+05       0.000000    6952.068767     335.074662
2021-12-05  1.396079e+06       0.000000  487021.690580  181599.490549
2021-12-12  1.218927e+06       0.000000   16947.468463  453625.156695
2021-12-19  1.034745e+06       0.000000  564323.280845     532.044602
2021-12-26  1.138998e+06       0.000000   26091.491744  296010.333143

[208 rows x 4 columns]

 

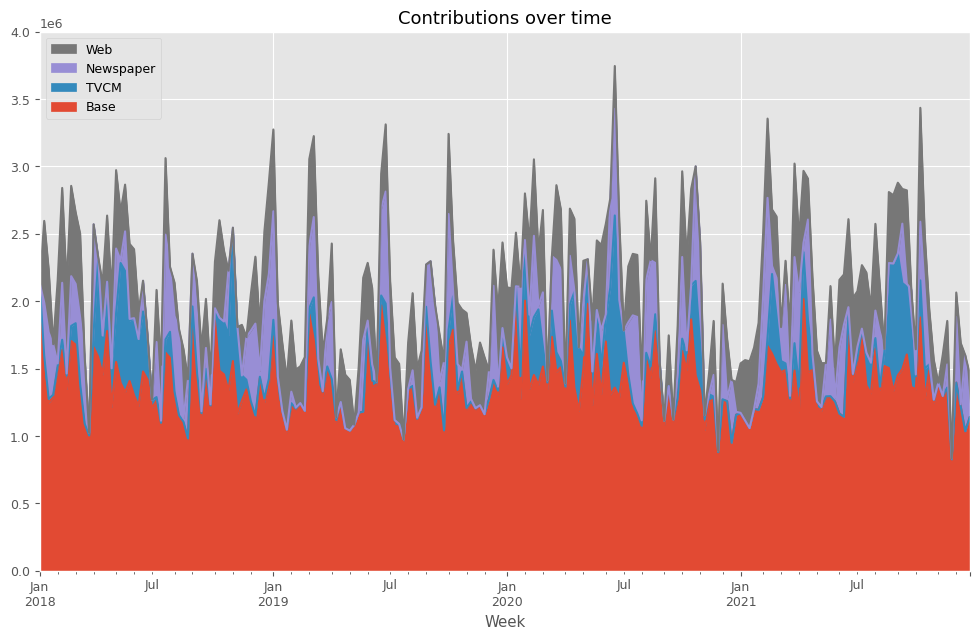
次に、貢献度の割合を計算します。

以下、コードです。

# 貢献度構成比の算出
contribution_results = summarize_and_plot_contribution(contribution)

 

以下、実行結果です。

           contribution     ratio
Base       2.865689e+08  0.653437
TVCM       3.259302e+07  0.074319
Newspaper  4.818772e+07  0.109878
Web        7.120648e+07  0.162366

 

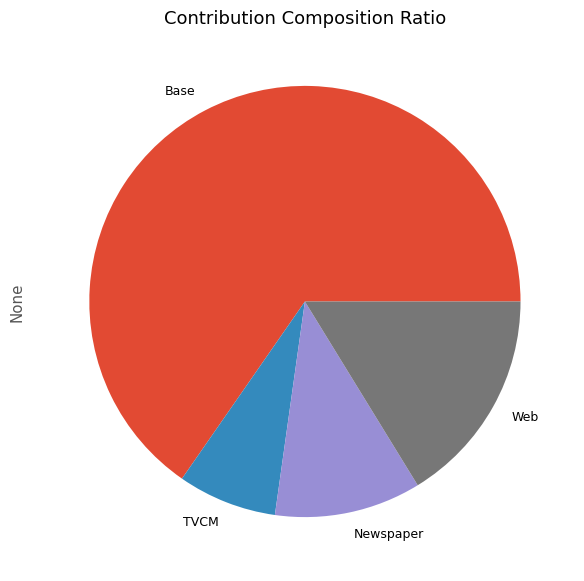
最後に、各メディアのマーケティングROIを計算します。

以下、コードです。

# マーケティングROIの算出
ROI = calculate_marketing_roi(X, contribution)

 

以下、実行結果です。

TVCM        -0.439477
Newspaper    0.047873
Web          1.272840
dtype: float64

 

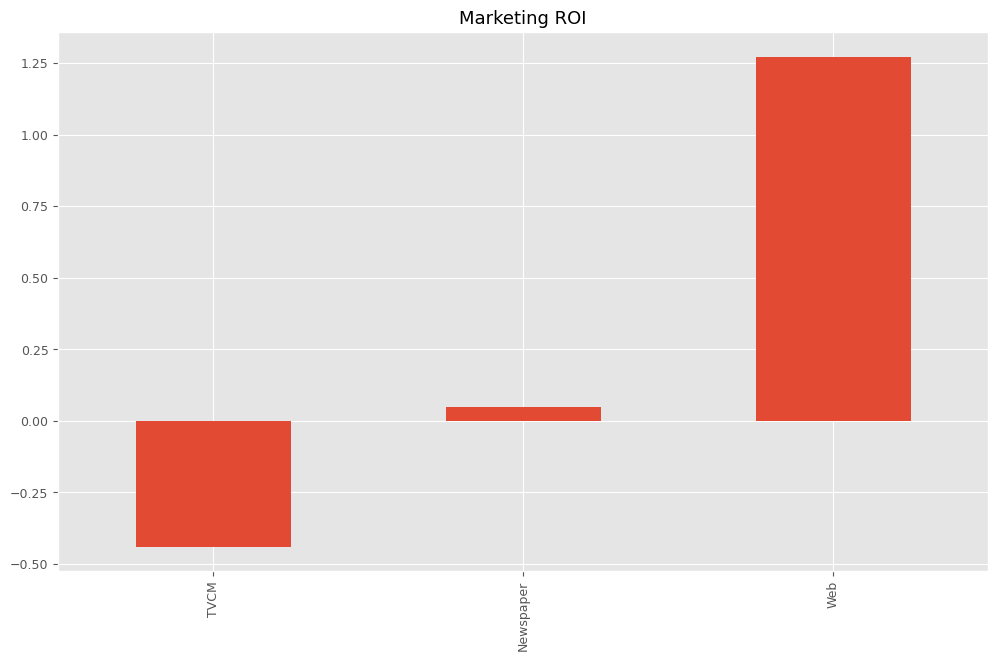
MMMパイプライン構築（ハイパーパラメータ自動調整）

　ハイパーパラメータ自動調整

ハイパーパラメータを自動チューニングするため、Optunaの目的関数を定義します。

以下、コードです。

def objective(trial, X, y):

    carryover_params = []
    curve_params = []
    n_features = X.shape[1]

    for i in X.columns:
        carryover_length = trial.suggest_int(f'carryover_length_{i}', 1, 10)
        carryover_peak = trial.suggest_int(f'carryover_peak_{i}', 1, carryover_length)
        carryover_rate1 = trial.suggest_float(f'carryover_rate1_{i}', 0, 1)
        carryover_rate2 = trial.suggest_float(f'carryover_rate2_{i}', 0, 1)
        carryover_c1 = trial.suggest_float(f'carryover_c1_{i}', 0, 2)
        carryover_c2 = trial.suggest_float(f'carryover_c2_{i}', 0, 2)
        carryover_params.append({
            'length': carryover_length, 
            'peak': carryover_peak, 
            'rate1': carryover_rate1, 
            'rate2': carryover_rate2, 
            'c1': carryover_c1, 
            'c2': carryover_c2,
        })

        curve_param_L = trial.suggest_float(f'curve_param_L_{i}', 0, 10)
        curve_param_k = trial.suggest_float(f'curve_param_k_{i}', 0, 10)
        curve_param_x0 = trial.suggest_float(f'curve_param_x0_{i}', 0, 2)
        curve_params.append({
            'L': curve_param_L,
            'k': curve_param_k,
            'x0': curve_param_x0,
        })

    alpha = trial.suggest_float('alpha', 1e-3, 1e+3)

    pipeline = Pipeline(steps=[
        ('scaler', MinMaxScaler()),
        ('carryover', CustomCarryOverTransformer(carryover_params=carryover_params)),
        ('saturation', CustomSaturationTransformer(curve_params=curve_params)),
        ('ridge', Ridge(alpha=alpha))
    ])

    tscv = TimeSeriesSplit(n_splits=5)
    scores = cross_val_score(pipeline, X, y, cv=tscv, scoring='neg_mean_squared_error')
    rmse = np.mean([np.sqrt(-score) for score in scores])

    return rmse

 

このコードは、機械学習モデルのハイパーパラメータ最適化に使用される関数objectiveを定義しています。

この関数は、提案されたハイパーパラメータセットを使用して構築されたパイプラインが、与えられたデータセットに対してどれだけよくフィットするかを評価し、RMSEを最小化する最適なハイパーパラメータセットを見つけます。

以下、引数です。

• trial: Optunaのトライアルオブジェクト。このオブジェクトを使用して、特定のトライアルで試すハイパーパラメータの値を提案します。
• X: モデルにフィットさせる特徴量（説明変数）のデータセット。
• y: モデルにフィットさせる目的変数。

以下、関数の中の処理の流れです。

• キャリオーバー効果パラメータの提案: 各特徴量について、キャリオーバー効果のパラメータ（長さ、ピーク、減衰率、曲線の形状パラメータ）を提案します。
• 飽和効果パラメータの提案: 同じく各特徴量について、飽和曲線（ロジスティック関数）のパラメータ（上限L、成長率k、中点x0）を提案します。
• リッジ回帰の正則化パラメータの提案: リッジ回帰モデルのalphaパラメータを提案します。このパラメータは、モデルの重みに対するL2正則化の強さを制御します。
• パイプラインの構築: MinMaxScaler、CustomCarryOverTransformer、CustomSaturationTransformer、そしてRidge回帰を含むパイプラインを構築します。
• クロスバリデーションの実行: 時系列データの分割を考慮したTimeSeriesSplitを使用してクロスバリデーションを実施し、ネガティブ平均二乗誤差をスコアリングメトリクスとして使用します。
• RMSEの計算: スコア（ネガティブ平均二乗誤差）の平方根を取ることで、クロスバリデーションの各スプリットから得られるRMSE（平均二乗誤差の平方根）を計算します。これは、モデルの予測精度を測る指標です。

Optunaを使用することで、このプロセスは自動的に多くの異なるハイパーパラメータの組み合わせを試し、最も性能が良い組み合わせを効率的に特定できます。これにより、手動でハイパーパラメータを調整する必要がなくなり、モデリングプロセスが大幅に加速します。

 

目的関数を最適化し、最適なハイパーパラメータを探索します。

以下、コードです。

# Optunaのスタディの作成と最適化の実行
study = optuna.create_study(direction='minimize')
objective_with_data = partial(objective, X=X, y=y)
study.optimize(objective_with_data, n_trials=5000)

print("Best trial:")
trial = study.best_trial

print(f"Value: {trial.value}")
print("Params: ")
for key, value in trial.params.items():
    print(f"{key}: {value}")

 

このコードは、目的関数（objective）に対する最適なハイパーパラメータセットを見つけるプロセスを示しています。

• スタディの作成:
  • optuna.create_study(direction='minimize')は、新しい最適化スタディを作成します。
  • direction='minimize'は、目的関数を最小化することを目標としています。
• 目的関数の準備:
  • objective_with_data = partial(objective, X=X, y=y)は、objective関数にデータセットXとターゲットyを予め組み込んだ部分適用（partial application）を作成します。
  • これにより、study.optimize()メソッドを呼び出す際に、毎回データセットを引数として渡す必要がなくなります。
• 最適化の実行:
  • study.optimize(objective_with_data, n_trials=5000)は、最適化プロセスを実行します。
  • ここで、n_trials=5000は、試行するハイパーパラメータのセットの数を指定しています。
  • Optunaはこれらの試行を通じて、目的関数が最小となるハイパーパラメータの組み合わせを探索します。
• 最適な試行の結果の表示:
  • スタディの最適化後、study.best_trialを使用して最良の試行（トライアル）を取得し、その試行の評価値（目的関数の最小値）と最適なハイパーパラメータのセットを表示します。
  • print(f"Value: {trial.value}")は、最適な試行の目的関数の値（例えば、最小のRMSE）を表示します。
  • その後、最適な試行で使用されたハイパーパラメータの各値をループして表示します。

 

以下、実行結果です。

Best trial:
Value: 172129.63296538804
Params: 
carryover_length_TVCM: 7
carryover_peak_TVCM: 1
carryover_rate1_TVCM: 0.5595718207601297
carryover_rate2_TVCM: 0.47968181853727276
carryover_c1_TVCM: 0.624117136238986
carryover_c2_TVCM: 0.9329166934441974
curve_param_L_TVCM: 2.616402720553469
curve_param_k_TVCM: 3.5547064268148594
curve_param_x0_TVCM: 0.009767632292007274
carryover_length_Newspaper: 2
carryover_peak_Newspaper: 1
carryover_rate1_Newspaper: 0.5335819616270121
carryover_rate2_Newspaper: 0.2903100600262293
carryover_c1_Newspaper: 1.9917224028084937
carryover_c2_Newspaper: 0.702828120189415
curve_param_L_Newspaper: 8.941607979346262
curve_param_k_Newspaper: 1.3671991272442934
curve_param_x0_Newspaper: 0.2998588329825045
carryover_length_Web: 1
carryover_peak_Web: 1
carryover_rate1_Web: 0.19610405654550517
carryover_rate2_Web: 0.6054493558532492
carryover_c1_Web: 0.9295203470571761
carryover_c2_Web: 1.9714922369045829
curve_param_L_Web: 7.25914552157673
curve_param_k_Web: 9.8178888298225
curve_param_x0_Web: 0.035387832529805874
alpha: 0.026684346105728035

 

最適なハイパーパラメータを使いMMMを構築するため、ハイパーパラメータの値を抽出し、以下のリストなどを作成します。

• best_carryover_params：キャリーオーバー効果関数のハイパーパラメータのリスト
• best_curve_params：飽和関数のハイパーパラメータのリスト
• best_alpha：Ridge回帰の正則化パラメータ

以下、コードです。

best_trial = study.best_trial

best_carryover_params = []
best_curve_params = []
n_features = X.shape[1]

for i in X.columns:
    best_carryover_params.append({
        'length': best_trial.params[f'carryover_length_{i}'],
        'peak': best_trial.params[f'carryover_peak_{i}'],
        'rate1': best_trial.params[f'carryover_rate1_{i}'],
        'rate2': best_trial.params[f'carryover_rate2_{i}'],
        'c1': best_trial.params[f'carryover_c1_{i}'],
        'c2': best_trial.params[f'carryover_c2_{i}']
    })
    
    best_curve_params.append({
        'L': best_trial.params[f'curve_param_L_{i}'],
        'k': best_trial.params[f'curve_param_k_{i}'],
        'x0': best_trial.params[f'curve_param_x0_{i}']
    })

best_alpha = best_trial.params['alpha']

 

このコードは、Optunaによる最適化プロセスの後、最適な試行（トライアル）からハイパーパラメータの最良のセットを抽出します。

• 最適な試行の取得:
  • best_trial = study.best_trialで、Optunaのスタディから最適な試行を取得します。
  • study.best_trialは、目的関数（objective）に対して最良の結果をもたらしたハイパーパラメータのセットです。
• キャリオーバー効果パラメータの抽出:
  • 各特徴量に対して、最適な試行からキャリオーバー効果に関連するハイパーパラメータ（長さ、ピーク、減衰率1と2、形状パラメータc1とc2）を抽出し、best_carryover_paramsリストに追加します。
• 飽和効果パラメータの抽出:
  • 同様に、各特徴量に対して、最適な試行から飽和効果をモデル化するためのロジスティック関数のパラメータ（L、k、x0）を抽出し、best_curve_paramsリストに追加します。
• リッジ回帰の正則化パラメータの抽出:
  • best_alpha = best_trial.params['alpha']で、最適な試行からリッジ回帰モデルの正則化強度alphaを取得します。

 

キャリーオーバー効果関数のハイパーパラメータのリストであるbest_carryover_paramsと、飽和関数のハイパーパラメータのリストであるbest_curve_paramsから、どのようなアドストック（キャリーオーバー効果関数と飽和関数）になったのかをグラフで確認してみます。

以下、コードです。

# グラフで確認
plot_effects(best_carryover_params, best_curve_params, X.columns)

 

以下、実行結果です。

 

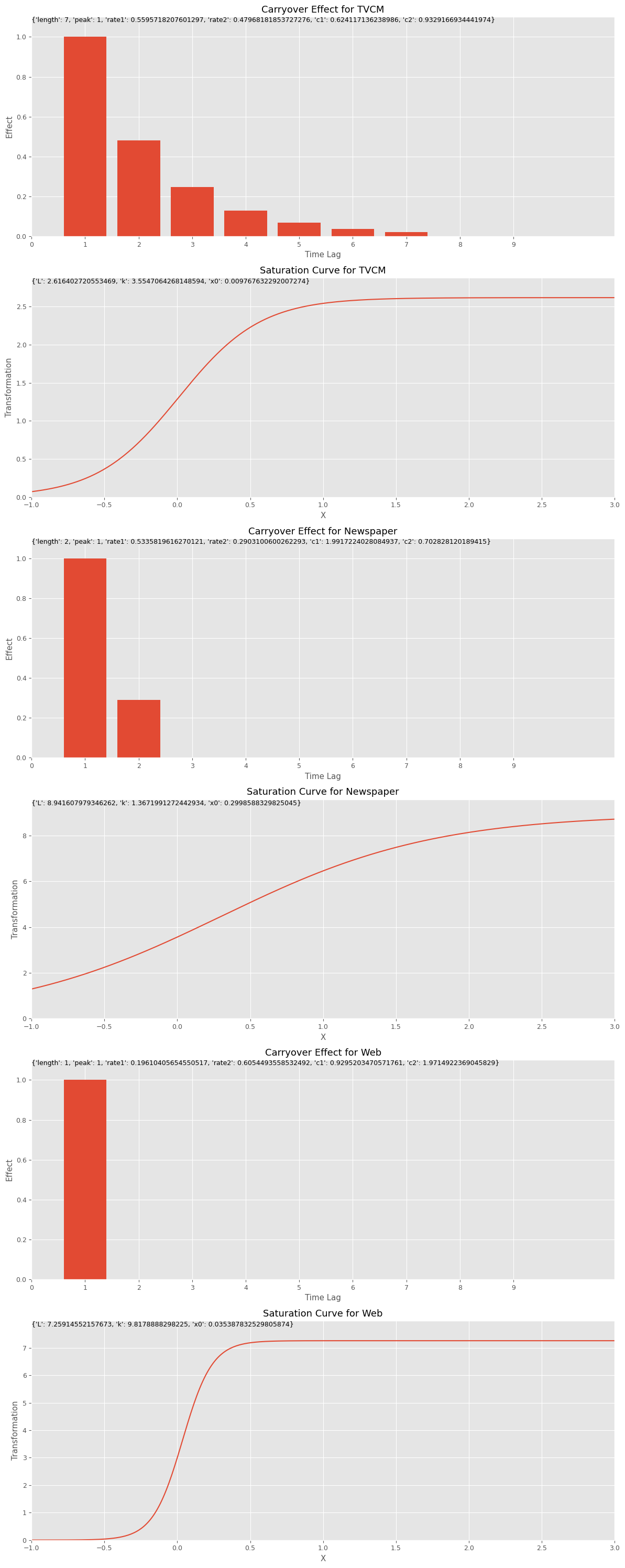
　MMM構築

このハイパーパラメータでMMMパイプラインを構築していきます。

以下、コードです。

# 最適なパイプラインの構築
MMM_pipeline = Pipeline(steps=[
    ('scaler', MinMaxScaler()),
    ('carryover', CustomCarryOverTransformer(carryover_params=best_carryover_params)),
    ('saturation', CustomSaturationTransformer(curve_params=best_curve_params)),
    ('ridge', Ridge(alpha=best_alpha))
])

 

このMMMパイプラインを学習し、実測と予測の散布図を描いてみます。

以下、コードです。

# パイプラインを使って学習
MMM_pipeline.fit(X, y)

# 学習したモデルを使って予測
predictions = MMM_pipeline.predict(X)

# 予測結果の表示
plt.figure(figsize=(10, 6))
plt.scatter(y, predictions)
plt.plot([y.min(), y.max()], [y.min(), y.max()], 'k--', lw=3)
plt.xlabel('actual')
plt.ylabel('predicted')
plt.title('Actual vs Predicted Values')
plt.show()

 

以下、実行結果です。

 

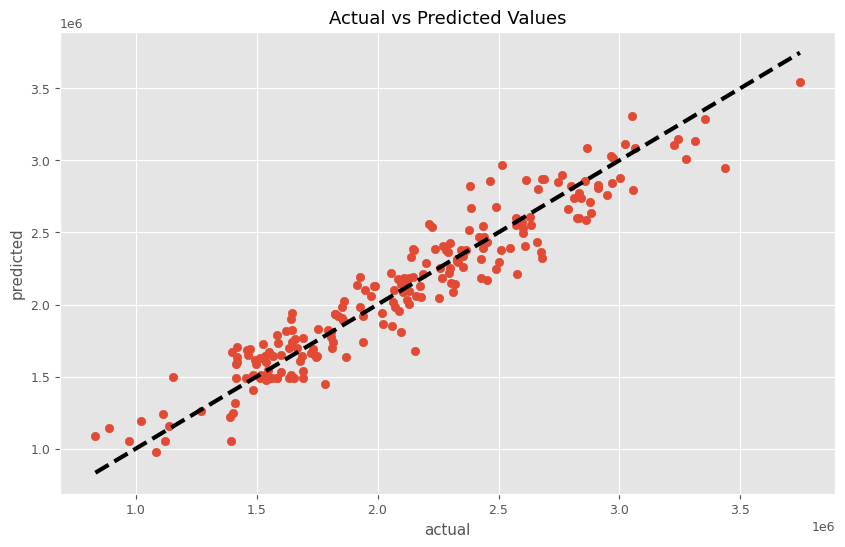
前回作った以下の関数群を使い、MMMモデル構築から貢献度算出、マーケティングROIの計算をしていきます。

関数train_and_evaluate_modelを使い、MMMを評価します。

以下、コードです。

# MMMの構築
trained_model, pred = train_and_evaluate_model(MMM_pipeline, X, y)

 

以下、実行結果です。

RMSE: 167411.59382956097
MAE: 134921.85480990302
MAPE: 0.06843416021526776
R2: 0.9100914470731689

 

ちなみに、以下は前回（シンプルなアドストックを考慮したMMM）の結果です。

RMSE: 175244.63286004536
MAE: 141136.68030802492
MAPE: 0.07014970643405759
R2: 0.9014811355562776

 

チューニングすることで、より良いMMMが構築できていることが分かります。

 

関数plot_actual_vs_predictedを使い、関数train_and_evaluate_modelで構築したMMMの予測値と実測値をプロットします。

以下、コードです。

# 実測値と予測値の時系列推移
plot_actual_vs_predicted(y.index, y.values, pred.y.values, (0, 4e6))

 

以下、実行結果です。

 

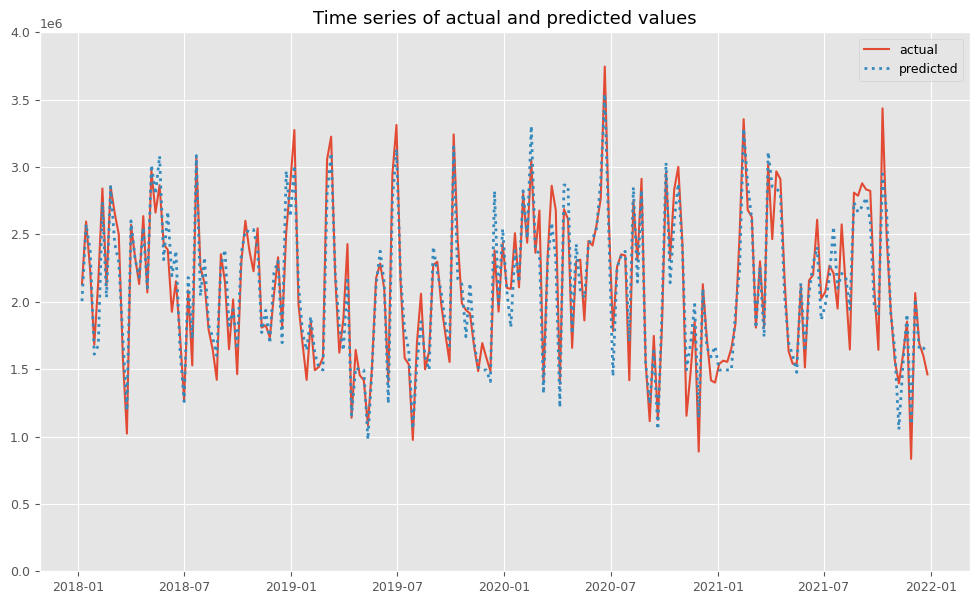
　後処理（結果の出力）

MMMを構築したら、貢献度やマーケティングROIなどを計算していきます。

先ずは、貢献度を計算します。

以下、コードです。

# 貢献度の算出
contribution = calculate_and_plot_contribution(y, X, trained_model,(0, 4e6))

 

以下、実行結果です。

                    Base          TVCM      Newspaper            Web
Week                                                                
2018-01-07  1.040070e+06  1.091930e+06       0.000000       0.000000
2018-01-14  9.860173e+05  5.733197e+05  516614.079327  520148.950818
2018-01-21  9.177332e+05  2.832417e+05  551516.817483  483708.300407
2018-01-28  1.020710e+06  1.667078e+05  493482.259539       0.000000
2018-02-04  1.256722e+06  1.094952e+05  126256.526144  662926.495846
...                  ...           ...            ...            ...
2021-11-28  7.479883e+05  0.000000e+00   85911.664756       0.000000
2021-12-05  1.000509e+06  0.000000e+00  538443.656408  525747.435447
2021-12-12  1.004818e+06  0.000000e+00  154950.004134  529732.232710
2021-12-19  9.478720e+05  0.000000e+00  651727.994075       0.000000
2021-12-26  8.464981e+05  0.000000e+00  168501.429481  446100.449586

[208 rows x 4 columns]

 

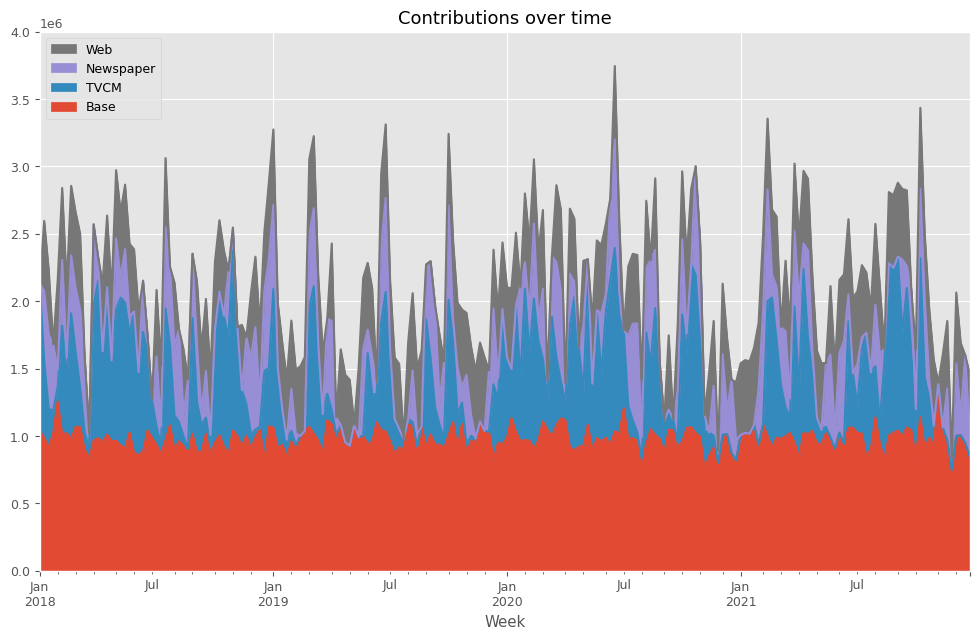
次に、貢献度の割合を計算します。

以下、コードです。

# 貢献度構成比の算出
contribution_results = summarize_and_plot_contribution(contribution)

 

以下、実行結果です。

           contribution     ratio
Base       2.034548e+08  0.463920
TVCM       9.417380e+07  0.214736
Newspaper  6.005176e+07  0.136931
Web        8.087571e+07  0.184414

 

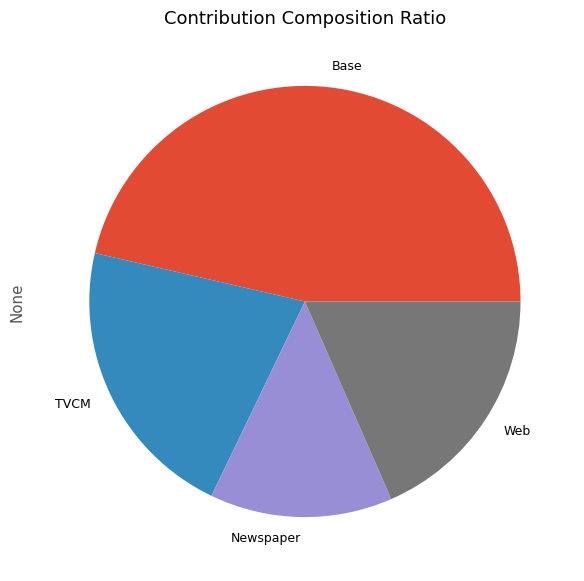
最後に、各メディアのマーケティングROIを計算します。

以下、コードです。

# マーケティングROIの算出
ROI = calculate_marketing_roi(X, contribution)

 

以下、実行結果です。

TVCM         0.619567
Newspaper    0.305865
Web          1.581472
dtype: float64

 

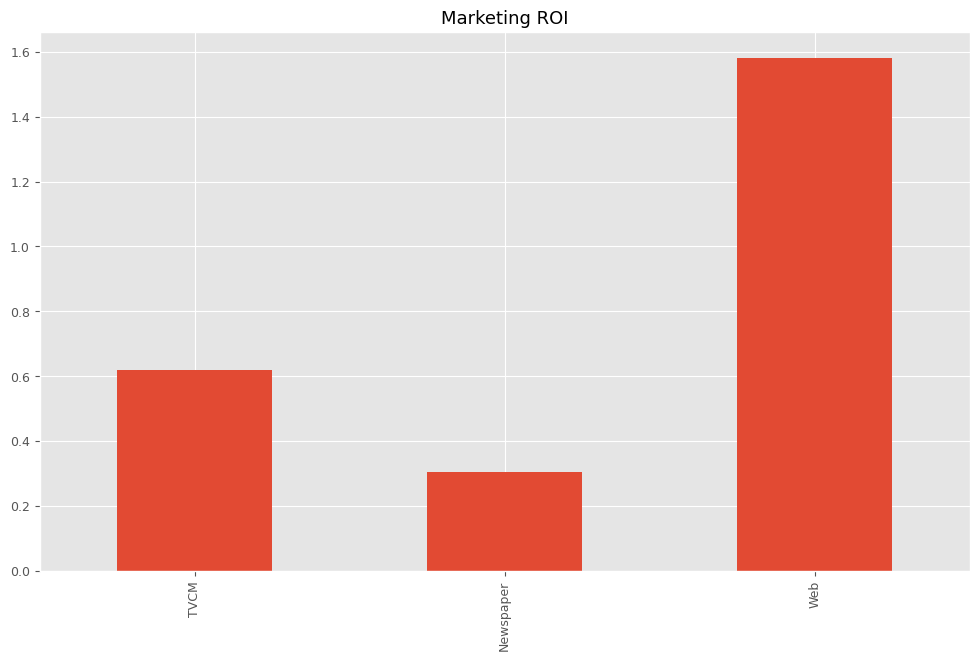
まとめ

今回は、以下のようなピークが広告販促媒体によって変化するなど、やや一般的なアドストック（上がキャリオーバー効果関数、下が飽和関数）で、MMMを構築するお話しをしました。

アドストックを表現するキャリーオーバー効果関数や飽和関数を、柔軟に表現できる関数にすることで、より良いMMMを構築できます。

ただ、柔軟に表現できる関数ほどハイパーパラメータが増え、それだけOptunaのトライアル回数を増やす必要があります。トライアル回数を増やすと、それだけ時間が掛かります。

 

今回のキャリーオーバー効果関数は、前回のキャリーオーバー効果関数を一般化したものなので、要は前回のキャリーオーバー効果関数を包含しています。

一方、飽和関数に関しては、そうではありません。前回の飽和関数（指数型）と、今回の飽和関数（ロジスティック型）は別物です。どちらがいいでしょうか。

 

次回は、アドストックの飽和関数を自動選択し構築するMMMというお話しをします。

要するに、アドストックのハイパーパラメータに、飽和関数の選択も含めます。

このように、色々な飽和関数やキャリオーバー関数を定義し、その中から選択するということができます。

PythonによるMMM（マーケティングミックスモデリング）とビジネス活用－ 振返り分析編（その5）：アドストック線形回帰系MMM（飽和関数自動選択） －