データを活用したマーケティング戦略は、ビジネスの成功に不可欠です。その中心に位置するのが、マーケティングミックスモデリング（MMM）です。

マーケティングミックスモデリング（MMM）は、過去のデータを分析する「振り返り分析」と未来のトレンドを予測する「近未来分析」の両方で有効に活用される強力なツールです。

 

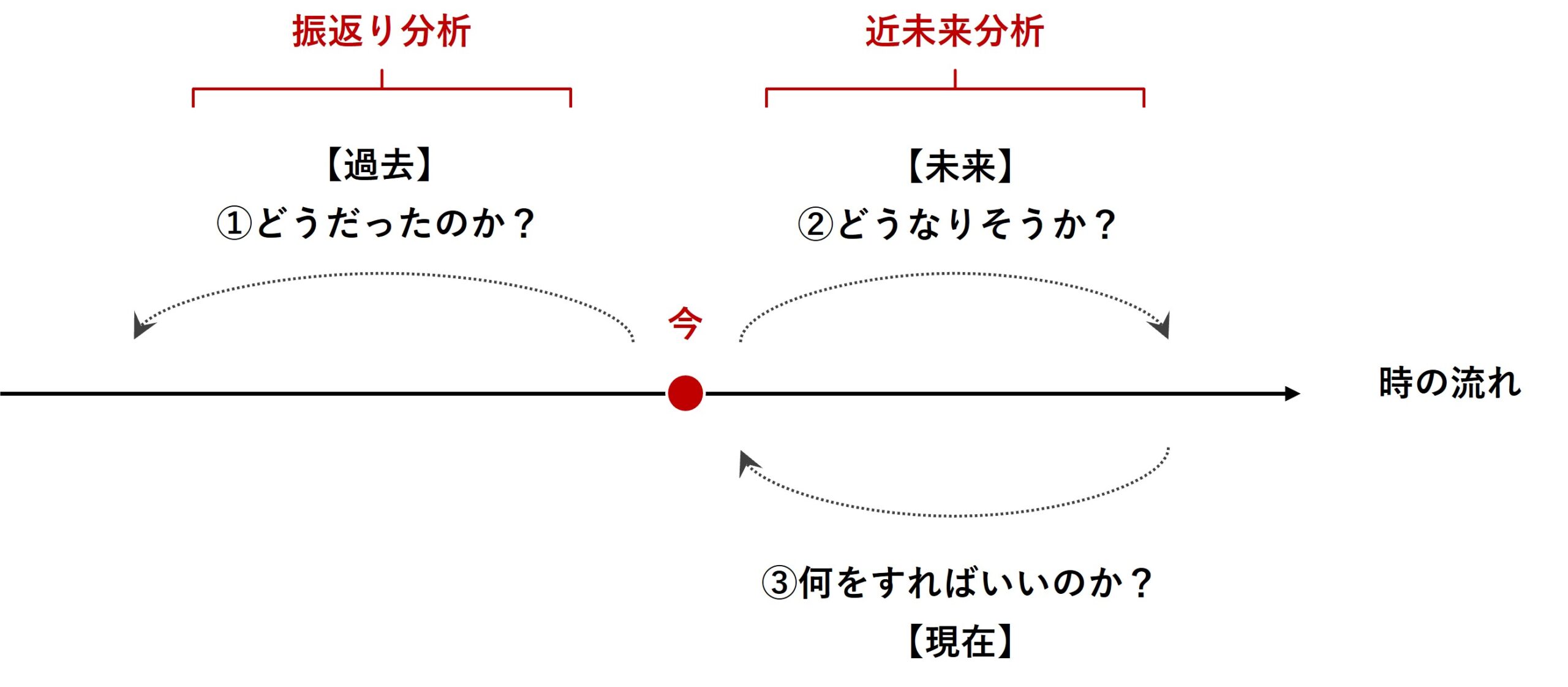
通常のMMMは、アドストック（Ad Stock）が考慮されます。ここで言うアドストック（Ad Stock）とは、キャリーオーバー効果や飽和効果のことです。

MMMにアドストック（Ad Stock）を組み込むには、パイプラインを構築するといいでしょう。このようなパイプラインを、ここではMMMパイプラインと表現することにします。

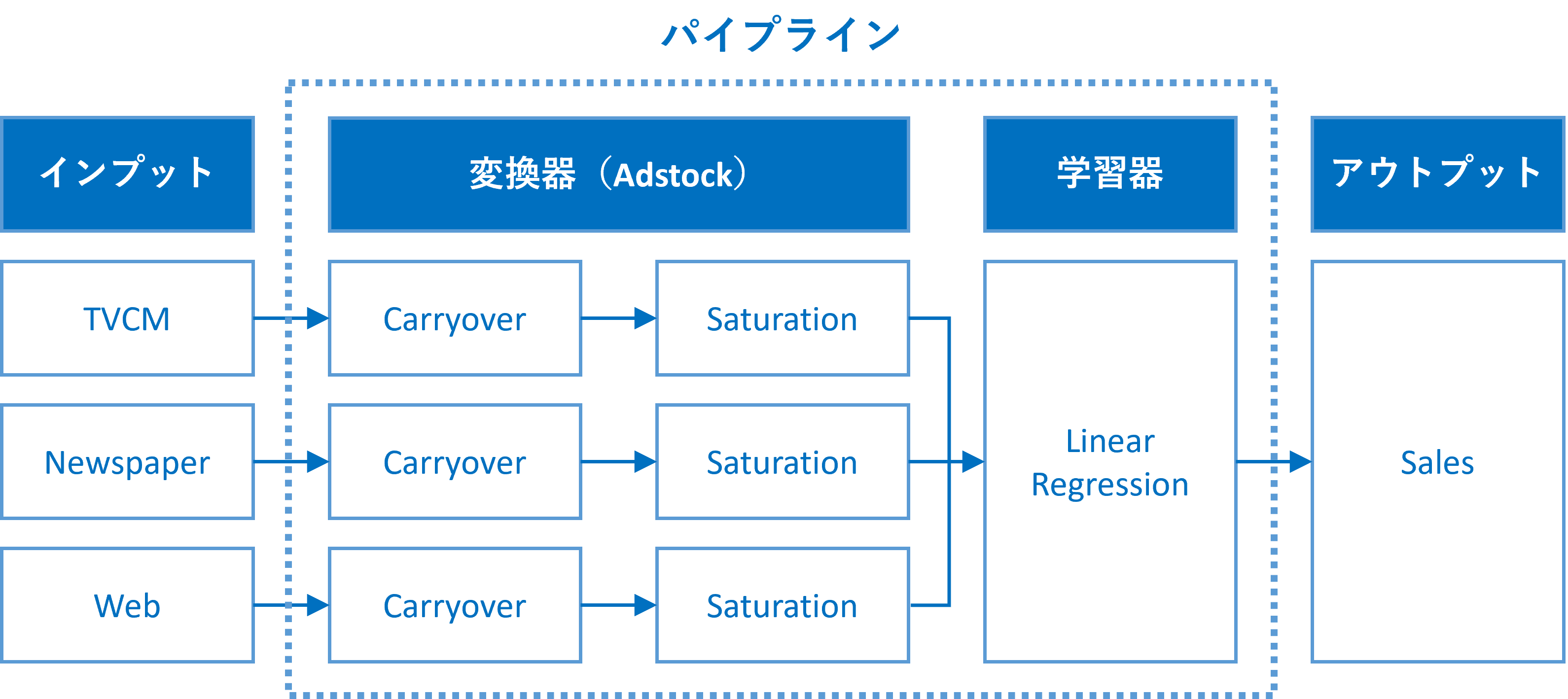
このMMMパイプラインは、少なくとも2つの変換器と1つの推定器が必要になります。

• 変換器
  • キャリーオーバー効果関数（Carryover）
  • 飽和関数（Saturation）
• 推定器
  • 線形回帰系のモデル（Linear Regression）：今回はRidge回帰を利用

 

飽和関数やキャリーオーバー効果関数には色々なものがあります。

前回は、アドストックの飽和関数を自動選択し構築するMMMというお話ししました。

PythonによるMMM（マーケティングミックスモデリング）とビジネス活用－ 振返り分析・線形回帰系モデル編（その4）－アドストック線形回帰系MMM（飽和関数自動選択）

具体的には、飽和関数（指数型）と飽和関数（ロジスティック型）のどちらかを自動選択できるように、アドストックのハイパーパラメータに、飽和関数の選択も含めました。

興味のある方は、前回の記事を参考に、色々な飽和関数やキャリーオーバー効果関数をPython上で定義し、各クラスに追加し遊んでみてください。

 

ただ、これだけだと変換器の自動選択・調整だけになってしまいます。

そこで今回は、ここに推定器の自動選択を含めたいと思います。

要するに、推定器自動選択を含めたMMMハイパーパラメータ自動調整です。

 

今回は、キャリーオーバー効果関数や飽和関数の説明はしません。気になる方は、前々回と前前々回の記事を一読ください。

また、コードの説明も、前回とほぼ同じコードについては説明をほぼ省きます。ただ、前回までに登場していないコードのみ説明を加えます。

今回利用する線形系モデル

MMMの推定器として、Pythonのscikit-learn（sklearn）の線形系のモデルでを利用します。

以下は、scikit-learn（sklearn）の線形回帰系のモデルの一部です（2024年1月24日現在）。

クラス名	特徴
LinearRegression	基本的な線形回帰モデル。最小二乗法を使用してパラメータを推定します。
Ridge	L2正則化を加えた線形回帰（リッジ回帰）。多重共線性を扱うのに適しています。
Lasso	L1正則化を加えた線形回帰。不要な特徴量の係数を0にし、スパースなモデルを作成します。
ElasticNet	L1とL2の両方の正則化を組み合わせたモデル。正則化のバランスが調整可能です。
Lars	最小角回帰。計算効率が良く、高次元データに適しています。
LassoLars	L1正則化を使用した最小角回帰。小さいデータセットに適しています。
OrthogonalMatchingPursuit	事前に定められた非ゼロ係数の数に基づいてモデルを作成します。
BayesianRidge	ベイジアンリッジ回帰。事前分布を用いて正則化されます。
ARDRegression	自動関連決定法（ARD）を使用したベイジアンリッジ回帰。
SGDRegressor	確率的勾配降下法を使用した線形モデル。大規模なデータセットに適しています。
PassiveAggressiveRegressor	オンライン学習に適したパッシブアグレッシブアルゴリズムを使用します。
RANSACRegressor	外れ値に強いモデルを作成するためのRANSACアルゴリズムを使用します。
TheilSenRegressor	外れ値に強く、中央値に基づく回帰を提供します。
HuberRegressor	外れ値に対して頑健な回帰モデル。Huber損失を使用します。
QuantileRegressor	分位数回帰を行います。データの特定の分位数に基づくモデルを作成します。
PLSRegression	部分的最小２乗回帰（Partial Least Squares Regression）。高次元データの次元削減や多重共線性問題に有効です。

 

使い分けなどに関しては、以下の記事を参考にしてください。

今回は、以下のscikit-learn（sklearn）の5つの線形系のモデルを使い、MMMを構築します。

• LinearRegression：一般的な線形回帰モデル
• Ridge：L2正則化を加えた線形回帰（リッジ回帰）
• BayesianRidge：ベイズ統計に基づいたリッジ回帰
• PLSRegression：部分的最小２乗回帰（Partial Least Squares Regression）
• 主成分回帰：PCAとLinearRegressionの組み合わせ

MMMのハイパーパラメータチューニングでは、この5つの推定器を選択し、さらに選択した推定器のハイパーパラメータ調整を含みます。

 

準備

今回利用するモジュールやデータセットの読み込み、先ほど述べたアドストック系関数の定義などを実施していきます。

 

　モジュールの読み込みや推定器リスト設定

　　モジュール

以下、コードです。

import numpy as np
import pandas as pd
import optuna

from sklearn.linear_model import Ridge

from sklearn.base import BaseEstimator, TransformerMixin
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import MinMaxScaler
from sklearn.model_selection import TimeSeriesSplit
from sklearn.model_selection import cross_val_score

from functools import partial

import warnings
warnings.simplefilter('ignore')

import matplotlib.pyplot as plt
plt.style.use('ggplot') #グラフスタイル
plt.rcParams['figure.figsize'] = [12, 7] #グラフサイズ
plt.rcParams['font.size'] = 9 #フォントサイズ

 

　　MMM推定器（およびパイプライン）のリスト

MMMとして利用するモデル（もしくはパイプライン）をリスト化します。

利用する

以下、コードです。

from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
from sklearn.linear_model import LinearRegression
from sklearn.linear_model import Ridge
from sklearn.linear_model import BayesianRidge
from sklearn.cross_decomposition import PLSRegression

estimators = [
    ("LR", LinearRegression()),
    ("Ridge", Ridge()), 
    ("BayesianRidge", BayesianRidge()),
    ("PLS", Pipeline([('scaler', StandardScaler()),
                      ("Reg", PLSRegression())
                    ])),
    ("PCR", Pipeline([('scaler', StandardScaler()),
                      ("PCA", PCA()), 
                      ("Reg", LinearRegression())
                    ]))
]

 

このリストは、MMM構築に利用する複数の異なる推定器（estimators）・パイプラインの一覧です。

• 線形回帰 (Linear Regression):
  • "LR", LinearRegression(): 標準的な線形回帰モデルです。特徴量とターゲット変数との間の線形関係をモデリングします。
• Ridge回帰:
  • "Ridge", Ridge(): Ridge回帰は線形回帰の一種で、正則化を含みます。正則化はモデルの複雑さを抑制し、過学習を防ぐのに役立ちます。
• ベイジアンRidge回帰:
  • "BayesianRidge", BayesianRidge(): ベイジアンアプローチを用いたRidge回帰です。モデルの重みに確率分布を使用し、不確実性をモデル化します。
• 部分最小二乗回帰 (PLS Regression):
  • "PLS", Pipeline([...]): 特徴量を標準化（StandardScaler）した後、PLSRegressionを適用するパイプラインです。PLSは、特徴量間の相関が高い場合に有用な手法です。
• 主成分回帰 (PCR: Principal Component Regression):
  • "PCR", Pipeline([...]): こちらもパイプラインで、特徴量を標準化した後、PCA（主成分分析）を適用し、その後線形回帰を行います。PCAは次元削減を行い、データの主要なパターンを抽出します。

 

　　以前作った関数群（MMM構築・評価など）

さらに今回は、以前作った以下の関数群を使います。

• MMM構築
  • train_and_evaluate_model:MMMの構築
  • plot_actual_vs_predicted:構築したMMMの予測値の時系列推移
• 後処理（結果の出力）
  • calculate_and_plot_contribution:売上貢献度の算出（時系列推移）
  • summarize_and_plot_contribution:売上貢献度構成比の算出
  • calculate_marketing_roi:マーケティングROIの算出

 

興味のある方、詳細を知りたい方は、以下を参照ください。

 

以下からダウンロードできます。

mmm_functions.py　※zipファイルを解凍してお使いください
https://www.salesanalytics.co.jp/oi17

 

mmm_functions.pyを利用するときは、実行するPythonファイルやNotebookと同じフォルダに入れておいてください。

以下のコードで呼び出せます。

from mmm_functions import *

 

上手くいかないときは、mmm_functions.pyをメモ帳などで開き内容をコピーし、実行するPythonファイルやNotebookにコードを張り付け、Pythonで関数を作ってからMMM構築などを行ってください。

 

　データセットの読み込み

以下、コードです。

# データセット読み込み
dataset = 'https://www.salesanalytics.co.jp/4zdt'
df = pd.read_csv(
    dataset,
    parse_dates=['Week'],
    index_col='Week',
)

# 説明変数Xと目的変数yに分解
X = df.drop(columns=['Sales'])
y = df['Sales']

 

目的変数y（売上）をプロットします。

以下、コードです。

y.plot()
plt.show()

 

以下、実行結果です。

 

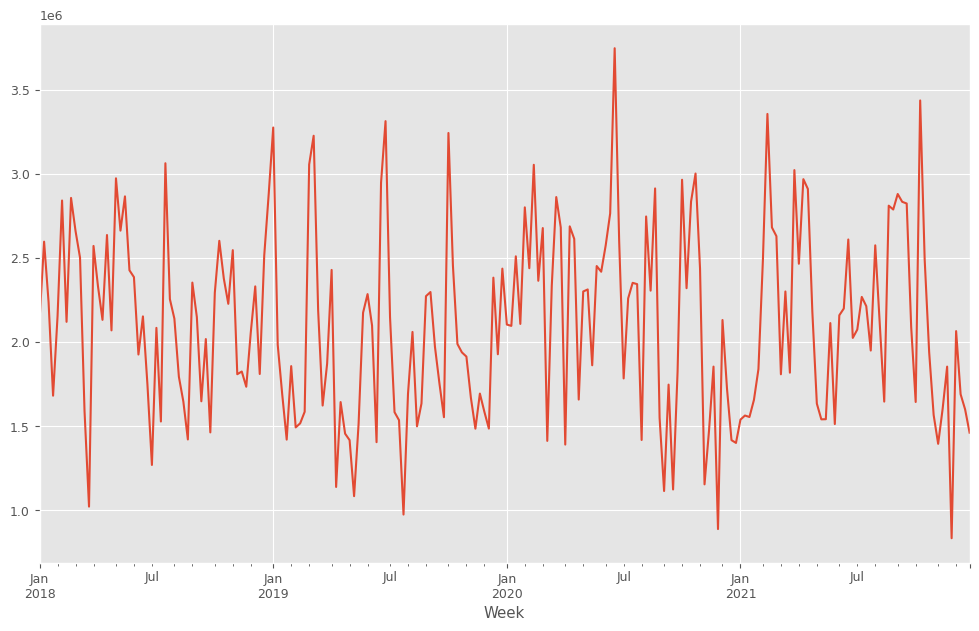
• y.plot(): y（目的変数）を折れ線グラフで表示します。plot()はPandasのデフォルトのグラフ化するためのプロット機能です。
• plt.show(): 作成されたグラフを画面に出力します。

 

説明変数X（各メディアのコスト）をまとめてプロットします。

以下、コードです。

X.plot(subplots=True)
plt.show()

 

以下、実行結果です。

 

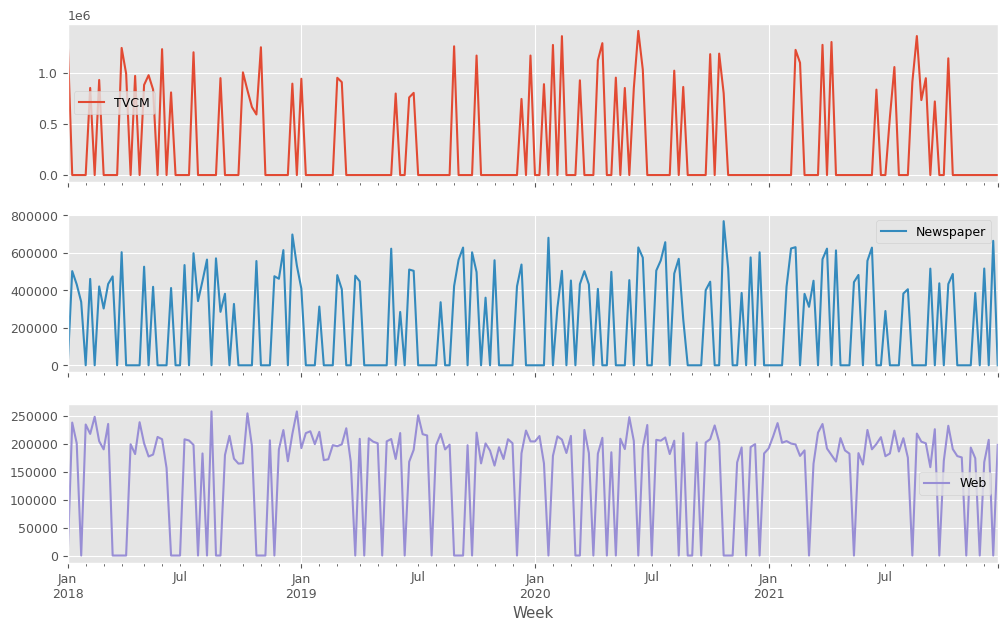
　アドストック系の関数とクラス、そのグラフ化関数の定義

アドストック系の関数である、シンプルなキャリーオーバー効果関数とそのクラス、シンプルな飽和関数とそのクラス、そしてそれらを視覚化（グラフ）する関数を作っていきます。

 

　　キャリオーバー効果関数

先ずは、キャリーオーバー効果関数とそのクラスを作ります。

以下、コードです。

# キャリオーバー効果関数
def carryover_advanced(X: np.ndarray, length, peak, rate1, rate2, c1, c2):
    X = np.append(np.zeros(length-1), X)
    
    Ws = np.zeros(length)
    
    for l in range(length):
        if l<peak-1:
            W = rate1**(abs(l-peak+1)**c1)
        else:
            W = rate2**(abs(l-peak+1)**c2)
        Ws[length-1-l] = W
    
    carryover_X = []
    
    for i in range(length-1, len(X)):
        X_array = X[i-length+1:i+1]
        Xi = sum(X_array * Ws)/sum(Ws)
        carryover_X.append(Xi)
        
    return np.array(carryover_X)

# キャリオーバー効果を適用するカスタム変換器クラス
class CustomCarryOverTransformer(BaseEstimator, TransformerMixin):
    def __init__(self, carryover_params=None):
        self.carryover_params = carryover_params if carryover_params is not None else []

    def fit(self, X, y=None):
        return self

    def transform(self, X):
        if isinstance(X, pd.DataFrame):
            X = X.to_numpy()
        transformed_X = np.copy(X)
        for i, params in enumerate(self.carryover_params):
            transformed_X[:, i] = carryover_advanced(X[:, i], **params)
        return transformed_X

 

　　飽和関数

次に、2つの飽和関数とそのクラスを作ります。

以下、コードです。

# 飽和関数（指数型）
def exponential_function(x, d):
    result = 1 - np.exp(-d * x)
    return result
    
# 飽和関数（ロジスティック曲線）
def logistic_function(x, L, k, x0):
    result = L / (1+ np.exp(-k*(x-x0)))  
    return result

# 飽和関数を適用するカスタム変換器クラス
class CustomSaturationTransformer(BaseEstimator, TransformerMixin):
    def __init__(self, curve_params=None):
        self.curve_params = curve_params if curve_params is not None else []
    def fit(self, X, y=None):
        return self
    def transform(self, X):
        if isinstance(X, pd.DataFrame):
            X = X.to_numpy()
        transformed_X = np.copy(X)
        for i, params in enumerate(self.curve_params):
            saturation_function = params.pop('saturation_function') 
            if saturation_function == 'logistic':
                transformed_X[:, i] = logistic_function(X[:, i], **params)
            elif saturation_function == 'exponential':
                transformed_X[:, i] = exponential_function(X[:, i], **params)
            params['saturation_function'] = saturation_function # Returning the saturation_function back to params
        return transformed_X

 

　　アドストック視覚化（グラフ）関数

どのようなアドストックになっているのかを視覚的に理解するために、視覚化（グラフ）する関数を作ります。

以下、コードです。

def plot_carryover_effect(params, feature_name, fig, axes, i):
    max_length = max(10, params['length'])
    x = np.concatenate(([1], np.zeros(max_length - 1)))
    y = carryover_advanced(x, **params)
    y = y / max(y) # Fixed line: y normalization moved here
    axes[2*i].bar(np.arange(1, max_length + 1), y)
    axes[2*i].set_title(f'Carryover Effect for {feature_name}')
    axes[2*i].text(0, 1.1, params, ha='left',va='top')
    axes[2*i].set_xlabel('Time Lag')
    axes[2*i].set_ylabel('Effect')
    axes[2*i].set_xticks(range(len(y)))
    axes[2*i].set_ylim(0, 1.1)

def plot_saturation_curve(params, feature_name, fig, axes, i):
    x = np.linspace(-1, 3, 400)
    saturation_function = params.pop('saturation_function') 
    if saturation_function == 'logistic':
        y = logistic_function(x, **params)
    elif saturation_function == 'exponential':
        y = exponential_function(x, **params)
    axes[2*i+1].plot(x, y, label=feature_name)
    axes[2*i+1].set_title(f'Saturation Curve for {feature_name}')
    params['saturation_function'] = saturation_function 
    axes[2*i+1].text(-1, max(y)* 1.1, params, ha='left',va='top')
    axes[2*i+1].set_xlabel('X')
    axes[2*i+1].set_ylabel('Transformation')
    axes[2*i+1].set_ylim(0, max(y) * 1.1)
    axes[2*i+1].set_xlim(-1, 3)

def plot_effects(carryover_params, curve_params, feature_names):
    fig, axes = plt.subplots(len(feature_names) * 2, 1, figsize=(12, 10*len(feature_names)))
    for i, params in enumerate(carryover_params):
        plot_carryover_effect(params, feature_names[i], fig, axes, i)
    for i, params in enumerate(curve_params):
        plot_saturation_curve(params, feature_names[i], fig, axes, i)
    plt.tight_layout()
    plt.show()

 

この関数を利用してみます。

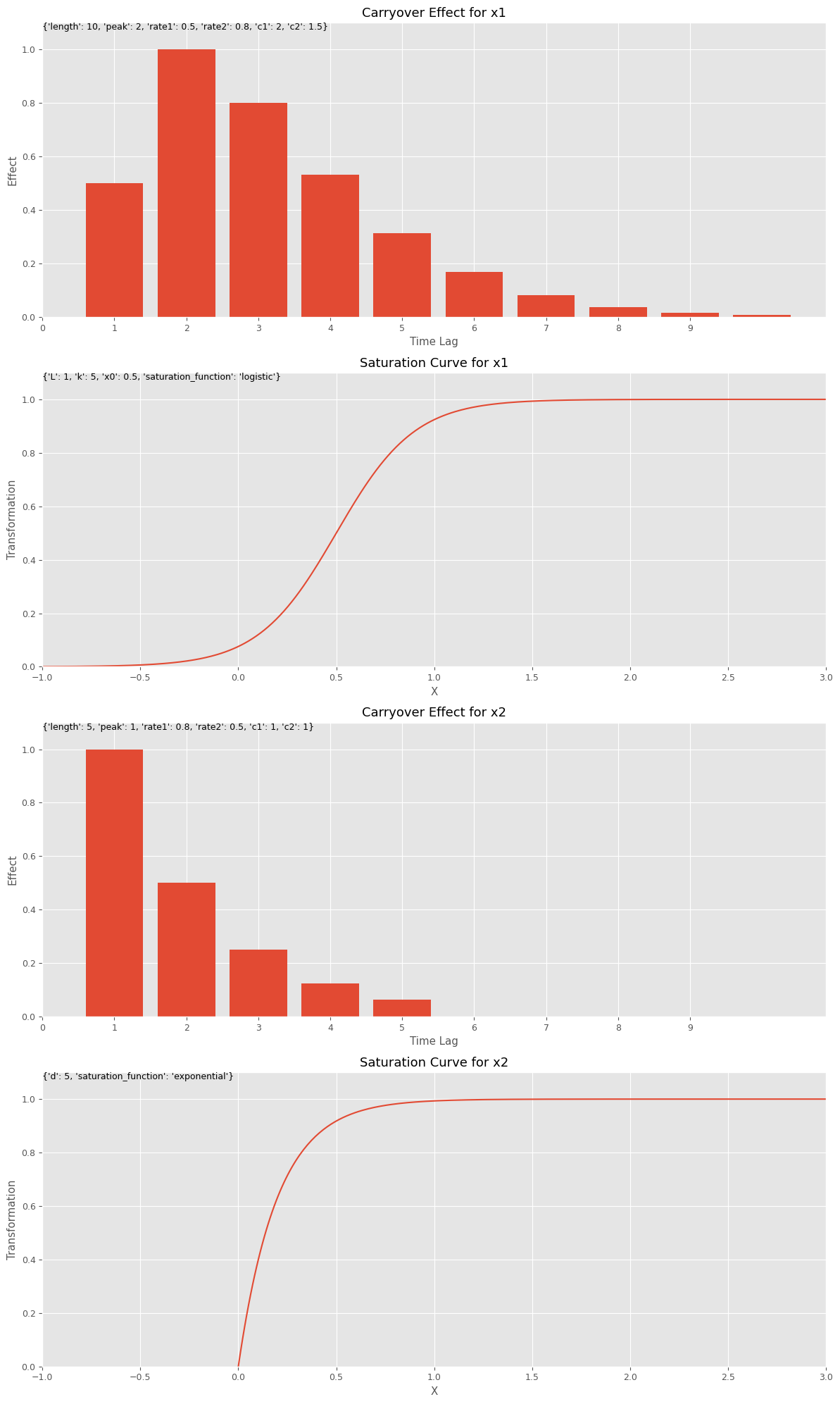
先ず、キャリーオーバー効果関数と飽和関数のハイパーパラメータを設定します。このハイパーパラメータを、今作った視覚化（グラフ）する関数にインプットしグラフを描きます。特徴量名は何を設定しても問題ございません。

以下、コードです。

# キャリーオーバー効果関数のハイパーパラメータの設定
carryover_params = [
    {'length': 10, 'peak': 2, 'rate1': 0.5, 'rate2': 0.8, 'c1': 2, 'c2': 1.5},
    {'length': 5, 'peak': 1, 'rate1': 0.8, 'rate2': 0.5, 'c1': 1, 'c2': 1}
]

# 飽和関数のハイパーパラメータの設定
curve_params = [
    {'saturation_function': 'logistic', 'L': 1, 'k': 5, 'x0': 0.5},
    {'saturation_function': 'exponential', 'd': 5}
]

# 特徴量名の設定
feature_names = ['x1', 'x2']

# グラフで確認
plot_effects(carryover_params, curve_params, feature_names)

 

以下、実行結果です。

 

MMMパイプライン構築（ハイパラ自動調整および推定器自動選択）

　ハイパーパラメータ自動調整

ハイパーパラメータを自動チューニングするため、Optunaの目的関数を定義します。

以下、コードです。

def objective(trial, X, y):

    carryover_params = []
    curve_params = []
    n_features = X.shape[1]

    # 推定器（もしくはパイプライン）の選択
    estimator_name = trial.suggest_categorical("estimator", [name for name, _ in estimators])
    estimator = next((est for name, est in estimators if name == estimator_name), None)

    if estimator_name == "LR":
        pass

    if estimator_name == "Ridge":
        alpha = trial.suggest_float("alpha_" + estimator_name, 0.01, 10) 
        estimator.set_params(alpha=alpha)

    if estimator_name == "BayesianRidge":
        alpha_1 = trial.suggest_float("alpha_1_" + estimator_name, 1e-6, 1e-3)
        alpha_2 = trial.suggest_float("alpha_2_" + estimator_name, 1e-6, 1e-3)
        lambda_1 = trial.suggest_float("lambda_1_" + estimator_name, 1e-6, 1e-3)
        lambda_2 = trial.suggest_float("lambda_2_" + estimator_name, 1e-6, 1e-3)
        estimator.set_params(
            alpha_1=alpha_1, alpha_2=alpha_2, lambda_1=lambda_1, lambda_2=lambda_2)

    if estimator_name == "PLS":
        n_comp = trial.suggest_int("n_comp_" + estimator_name, 1, X.shape[1])
        estimator.set_params(Reg__n_components=n_comp)

    if estimator_name == "PCR":
        n_comp = trial.suggest_int("n_comp_" + estimator_name, 1, X.shape[1])
        estimator.set_params(PCA__n_components=n_comp)

    # アドストック（キャリーオーバー効果関数・飽和関数）の選択
    for i in X.columns:
        carryover_length = trial.suggest_int(f'carryover_length_{i}', 1, 10)
        carryover_peak = trial.suggest_int(f'carryover_peak_{i}', 1, carryover_length)
        carryover_rate1 = trial.suggest_float(f'carryover_rate1_{i}', 0, 1)
        carryover_rate2 = trial.suggest_float(f'carryover_rate2_{i}', 0, 1)
        carryover_c1 = trial.suggest_float(f'carryover_c1_{i}', 0, 2)
        carryover_c2 = trial.suggest_float(f'carryover_c2_{i}', 0, 2)
        carryover_params.append({
            'length': carryover_length, 
            'peak': carryover_peak, 
            'rate1': carryover_rate1, 
            'rate2': carryover_rate2, 
            'c1': carryover_c1, 
            'c2': carryover_c2,
        })

        saturation_function = trial.suggest_categorical(f'saturation_function_{i}', ['logistic', 'exponential'])
        if saturation_function == 'logistic':
            curve_param_L = trial.suggest_float(f'curve_param_L_{i}', 0, 10)
            curve_param_k = trial.suggest_float(f'curve_param_k_{i}', 0, 10)
            curve_param_x0 = trial.suggest_float(f'curve_param_x0_{i}', 0, 2)
            curve_params.append({
                'saturation_function': saturation_function,
                'L': curve_param_L,
                'k': curve_param_k,
                'x0': curve_param_x0,
            })
        elif saturation_function == 'exponential':
            curve_param_d = trial.suggest_float(f'curve_param_d_{i}', 0, 10)
            curve_params.append({
                'saturation_function': saturation_function,
                'd': curve_param_d,
            })

    pipeline = Pipeline(steps=[
        ('scaler', MinMaxScaler()),
        ('carryover', CustomCarryOverTransformer(carryover_params=carryover_params)),
        ('saturation', CustomSaturationTransformer(curve_params=curve_params)),
        ('estimator', estimator)
    ])

    tscv = TimeSeriesSplit(n_splits=5)
    scores = cross_val_score(pipeline, X, y, cv=tscv, scoring='neg_mean_squared_error')
    rmse = np.mean([np.sqrt(-score) for score in scores])

    return rmse

 

このコードは、機械学習モデルのハイパーパラメータ最適化に使用される関数objectiveを定義しています。

以下、関数objectiveの概要です。

• 目的関数の定義
  • def objective(trial, X, y): この関数は、Optunaの試行（trial）と、特徴量（X）およびターゲット変数（y）を引数として受け取ります。
• 推定器の選択
  • estimator_name = trial.suggest_categorical("estimator", [name for name, _ in estimators]): ここでは、試行で使用する推定器（機械学習モデル）をカテゴリカル変数として選択します。estimatorsは、名前と推定器オブジェクトのペアのリストです。
  • estimator = next((est for name, est in estimators if name == estimator_name), None): 選択された名前に基づいて、estimatorsリストから対応する推定器を取得します。
• 推定器のハイパーパラメータの設定
  • このコードでは、選択された推定器に応じて、異なるハイパーパラメータを最適化します。
  • 例えば、Ridge回帰ではalphaパラメータ、BayesianRidgeではalpha_1、alpha_2、lambda_1、lambda_2が最適化されます。
• キャリーオーバー効果と飽和関数のモデリング
  • 各特徴量について、キャリーオーバー効果の長さ、ピーク、レート、および係数を最適化します。
  • 飽和関数としてlogisticまたはexponentialを選択し、それぞれのパラメータを最適化します。
• パイプラインの構築
  • MinMaxScalerを使用して特徴量をスケーリングし、CustomCarryOverTransformerとCustomSaturationTransformerを使用してキャリーオーバー効果と飽和効果をモデルに組み込み、最後に選択された推定器を適用します。
• モデル評価
  • TimeSeriesSplitを使用して時系列データのクロスバリデーションを行い、cross_val_scoreを用いてモデルのRMSEを計算します。
• 戻り値
  • 最終的に、この関数はRMSEの平均値を返します。Optunaはこの戻り値を使用して、ハイパーパラメータのセットを最適化します。

 

目的関数を最適化し、最適なハイパーパラメータを探索します。

以下、コードです。

# Optunaのスタディの作成と最適化の実行
study = optuna.create_study(direction='minimize')
objective_with_data = partial(objective, X=X, y=y)
study.optimize(objective_with_data, n_trials=10000)

print("Best trial:")
trial = study.best_trial

print(f"Value: {trial.value}")
print("Params: ")
for key, value in trial.params.items():
    print(f"{key}: {value}")

 

以下、実行結果です。

Best trial:
Value: 169725.97702363675
Params: 
estimator: LR
carryover_length_0: 5
carryover_peak_0: 1
carryover_rate1_0: 0.10589048336223184
carryover_rate2_0: 0.49132159234310613
carryover_c1_0: 0.3952755118981127
carryover_c2_0: 0.8849866225732939
saturation_function_0: logistic
curve_param_L_0: 8.901647599715456
curve_param_k_0: 4.688747656035356
curve_param_x0_0: 0.1615714911813316
carryover_length_1: 5
carryover_peak_1: 1
carryover_rate1_1: 0.732292954394962
carryover_rate2_1: 0.3000526454389536
carryover_c1_1: 0.5572980909313391
carryover_c2_1: 1.9987051639172833
saturation_function_1: logistic
curve_param_L_1: 9.580747152121312
curve_param_k_1: 0.30391622082462966
curve_param_x0_1: 1.8159637581580392
carryover_length_2: 1
carryover_peak_2: 1
carryover_rate1_2: 0.1626886492939998
carryover_rate2_2: 0.7354172971869495
carryover_c1_2: 0.18022645379815744
carryover_c2_2: 0.44563250019929823
saturation_function_2: exponential
curve_param_d_2: 1.5987276387335245

 

　MMM構築

最適なハイパーパラメータを使いMMMを構築します。

先ず、そのための関数を定義します。

以下、コードです。

def create_model_from_trial(trial, estimators):
    carryover_params = []
    curve_params = []
    n_features = X.shape[1]

    carryover_keys = ['length', 'peak', 'rate1', 'rate2', 'c1', 'c2']
    curve_keys_logistic = ['L', 'k', 'x0']
    curve_keys_exponential = ['d']

    # ハイパーパラメータを抽出しキーと値の辞書を作成する関数
    def fetch_params(prefix, index, params, trial_params):
        return {key: trial_params[f'{prefix}_{key}_{index}'] for key in params}

    # キャリーオーバー関数ハイパーパラメーターを取得
    carryover_params = [fetch_params('carryover', i, carryover_keys, trial.params) for i in X.columns]

    # 飽和関数ハイパーパラメーターを取得
    for i in X.columns:
        saturation_function = trial.params[f'saturation_function_{i}']
        curve_param = {'saturation_function': saturation_function}
        
        if saturation_function == 'logistic':
            curve_param.update(fetch_params('curve_param', i, curve_keys_logistic, trial.params))
        elif saturation_function == 'exponential':
            curve_param.update(fetch_params('curve_param', i, curve_keys_exponential, trial.params))
        
        curve_params.append(curve_param)

    # 推定器ハイパーパラメーターを取得
    best_estimator_name = trial.params['estimator']
    best_estimator = next((est for name, est in estimators if name == best_estimator_name), None)

    if best_estimator_name == "Ridge":
        alpha = trial.params.get('alpha_Ridge', 1.0)
        best_estimator.set_params(alpha=alpha)

    elif best_estimator_name == "BayesianRidge":
        best_estimator.set_params(
            alpha_1=trial.params['alpha_1_BayesianRidge'],
            alpha_2=trial.params['alpha_2_BayesianRidge'],
            lambda_1=trial.params['lambda_1_BayesianRidge'],
            lambda_2=trial.params['lambda_2_BayesianRidge']
        )

    elif best_estimator_name == "PLS":
        n_comp = trial.params['n_comp_PLS']
        best_estimator.set_params(Reg__n_components=n_comp)

    elif best_estimator_name == "PCR":
        n_comp = trial.params['n_comp_PCR']
        best_estimator.set_params(PCA__n_components=n_comp)

    # パイプラインを作成
    MMM_pipeline = Pipeline(steps=[
        ('scaler', MinMaxScaler()),
        ('carryover', CustomCarryOverTransformer(carryover_params=carryover_params)),
        ('saturation', CustomSaturationTransformer(curve_params=curve_params)),
        ('estimator', best_estimator)
    ])

    return MMM_pipeline,carryover_params,curve_params

 

このコードは、Optunaによる試行結果（trial）と推定器のリスト（estimators）を使用して、機械学習モデルのパイプラインを生成する関数create_model_from_trialを定義しています。

以下、関数create_model_from_trialの概要です。

• ハイパーパラメータ抽出関数
  • fetch_params関数は、特定のハイパーパラメータ群に対して、試行からキーと値のペアを抽出して辞書を作成するために使用されます。
  • これにより、キャリーオーバー効果と飽和効果のパラメータを効率的に取得できます。
• キャリーオーバー効果パラメータの取得
  • 試行結果（trial）からキャリーオーバー効果のパラメータを取得しcarryover_paramsリストを作成する。
  • これらはfetch_params関数を使用して取得されます。
• 飽和効果パラメータの取得
  • 試行結果（trial）から飽和効果のパラメータを取得しcurve_paramsリストを作成する。
  • これらはfetch_params関数を使用して取得されます。
• 推定器の選択と設定
  • 試行結果（trial）から最適な推定器を取得しbest_estimator_nameに設定する。
  • best_estimator_nameに対応するハイパーパラメータを試行結果（trial）から取得し推定器を構成します。
• パイプラインの構築
  • 最終的に、MinMaxScaler、CustomCarryOverTransformer、CustomSaturationTransformer、および最適化された推定器を含むパイプラインMMM_pipelineが作成されます。
  • このパイプラインはMMMパイプラインです。
• 戻り値
  • 最適なハイパーパラメータで設定したMMMパイプラインMMM_pipeline
  • キャリオーバー効果に関連するハイパーパラメータのリストcarryover_params
  • 飽和関数に関連するハイパーパラメータのリストcurve_params

 

では、この関数を実行します。

以下、コードです。

MMM_pipeline,best_carryover_params,best_curve_params = create_model_from_trial(study.best_trial, estimators)

 

以下が出力されます。

• 最適なハイパーパラメータで設定したMMMパイプラインMMM_pipeline
• キャリオーバー効果に関連するハイパーパラメータのリストcarryover_params
• 飽和関数に関連するハイパーパラメータのリストcurve_params

 

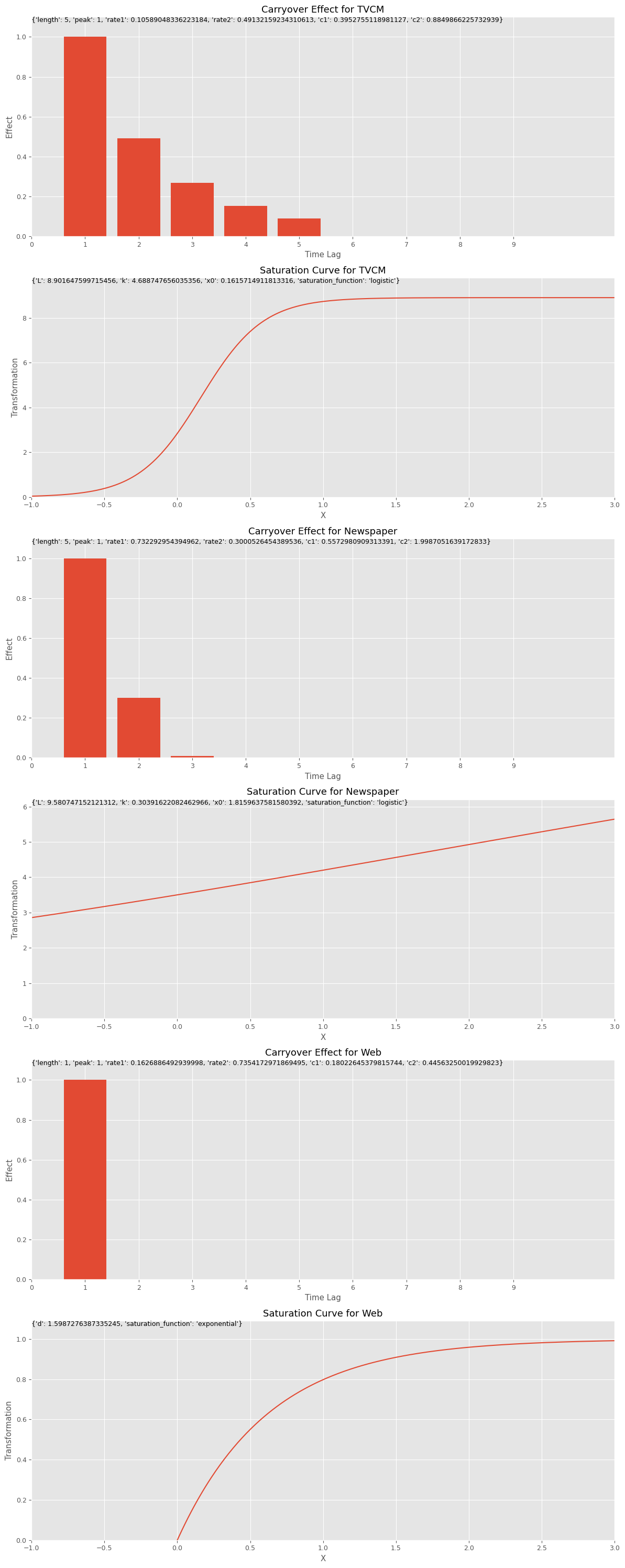
キャリーオーバー効果関数のハイパーパラメータのリストであるbest_carryover_paramsと、飽和関数のハイパーパラメータのリストであるbest_curve_paramsから、どのようなアドストック（キャリーオーバー効果関数と飽和関数）になったのかをグラフで確認してみます。

以下、コードです。

# グラフで確認
plot_effects(best_carryover_params, best_curve_params, X.columns)

 

以下、実行結果です。

 

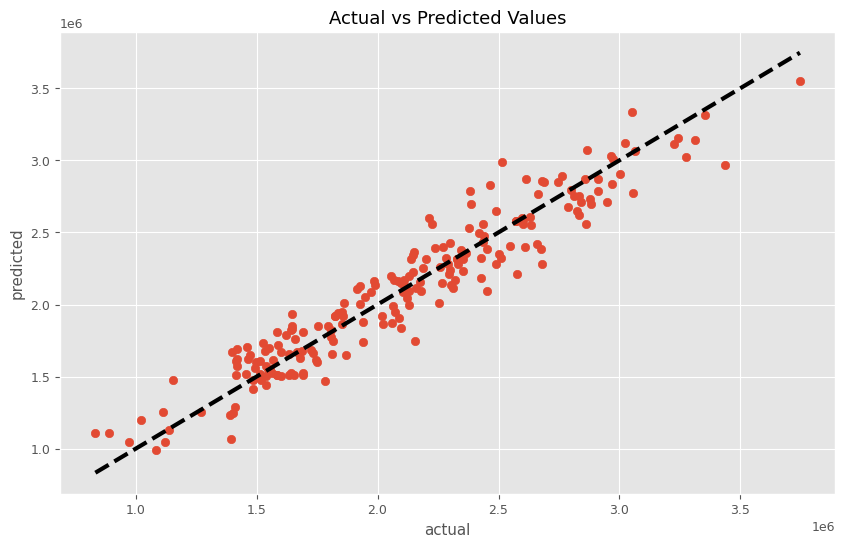
関数create_model_from_trialの出力である、MMMパイプラインMMM_pipelineを学習し、実測と予測の散布図を描いてみます。

以下、コードです。

# パイプラインを使って学習
MMM_pipeline.fit(X, y)

# 学習したモデルを使って予測
predictions = MMM_pipeline.predict(X)

# 予測結果の表示
plt.figure(figsize=(10, 6))
plt.scatter(y, predictions)
plt.plot([y.min(), y.max()], [y.min(), y.max()], 'k--', lw=3)
plt.xlabel('actual')
plt.ylabel('predicted')
plt.title('Actual vs Predicted Values')
plt.show()

 

以下、実行結果です。

 

以前作った以下の関数群を使い、MMMモデル構築から貢献度算出、マーケティングROIの計算をしていきます。

• MMM構築
  • train_and_evaluate_model:MMMの構築
  • plot_actual_vs_predicted:構築したMMMの予測値の時系列推移
• 後処理（結果の出力）
  • calculate_and_plot_contribution:売上貢献度の算出（時系列推移）
  • summarize_and_plot_contribution:売上貢献度構成比の算出
  • calculate_marketing_roi:マーケティングROIの算出

 

繰り返しの説明になります。

以下からダウンロードできます。

mmm_functions.py　※zipファイルを解凍してお使いください
https://www.salesanalytics.co.jp/oi17

 

mmm_functions.pyを利用するときは、実行するPythonファイルやNotebookと同じフォルダに入れておいてください。

以下のコードで呼び出せます。

from mmm_functions import *

 

上手くいかないときは、mmm_functions.pyをメモ帳などで開き内容をコピーし、実行するPythonファイルやNotebookにコードを張り付け、Pythonで関数を作ってからMMM構築などを行ってください。

 

関数train_and_evaluate_modelを使い、MMMを評価します。

以下、コードです。

# MMMの構築
trained_model, pred = train_and_evaluate_model(MMM_pipeline, X, y)

 

以下、実行結果です。

RMSE: 164512.17181288122
MAE: 131670.9125887425
MAPE: 0.06675659805783914
R2: 0.9131787534280218

 

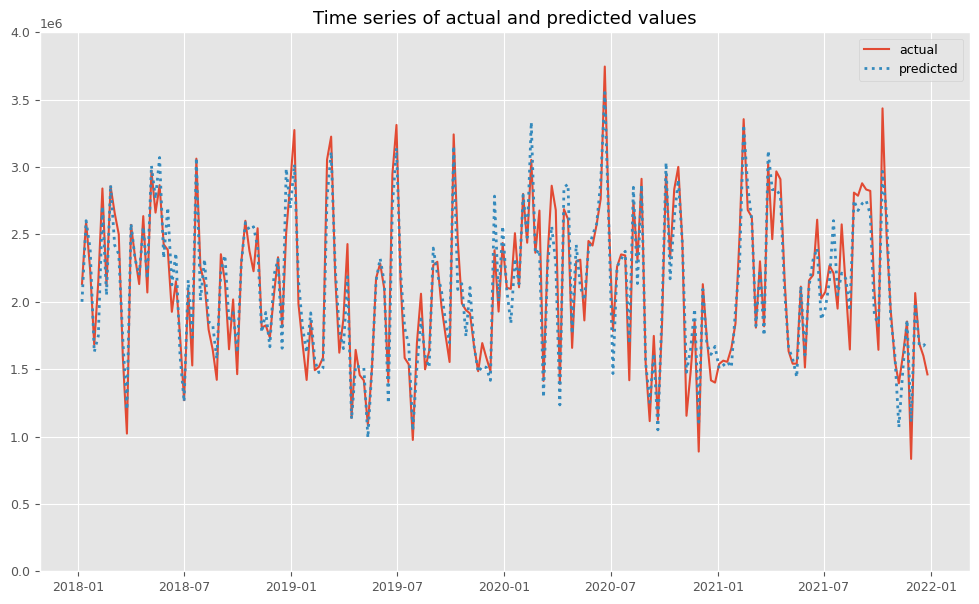
関数plot_actual_vs_predictedを使い、関数train_and_evaluate_modelで構築したMMMの予測値と実測値をプロットします。

以下、コードです。

# 実測値と予測値の時系列推移
plot_actual_vs_predicted(y.index, y.values, pred.y.values, (0, 4e6))

 

以下、実行結果です。

 

　後処理（結果の出力）

MMMを構築したら、貢献度やマーケティングROIなどを計算していきます。

先ずは、貢献度を計算します。

以下、コードです。

# 貢献度の算出
contribution = calculate_and_plot_contribution(y, X, trained_model,(0, 4e6))

 

以下、実行結果です。

                    Base          TVCM      Newspaper            Web
Week                                                                
2018-01-07  1.056189e+06  1.075811e+06       0.000000       0.000000
2018-01-14  9.885539e+05  5.349900e+05  508476.810590  564079.292136
2018-01-21  9.262309e+05  2.679765e+05  553762.603615  488230.067639
2018-01-28  1.023691e+06  1.633728e+05  493836.381702       0.000000
2018-02-04  1.222133e+06  1.108809e+05  129441.871342  692944.164139
...                  ...           ...            ...            ...
2021-11-28  7.466223e+05  0.000000e+00   87277.729371       0.000000
2021-12-05  1.027528e+06  0.000000e+00  546641.949073  490530.096815
2021-12-12  9.988154e+05  0.000000e+00  156416.352358  534268.238256
2021-12-19  9.478341e+05  0.000000e+00  651765.863348       0.000000
2021-12-26  8.470880e+05  0.000000e+00  170890.762809  443121.227157

[208 rows x 4 columns]

 

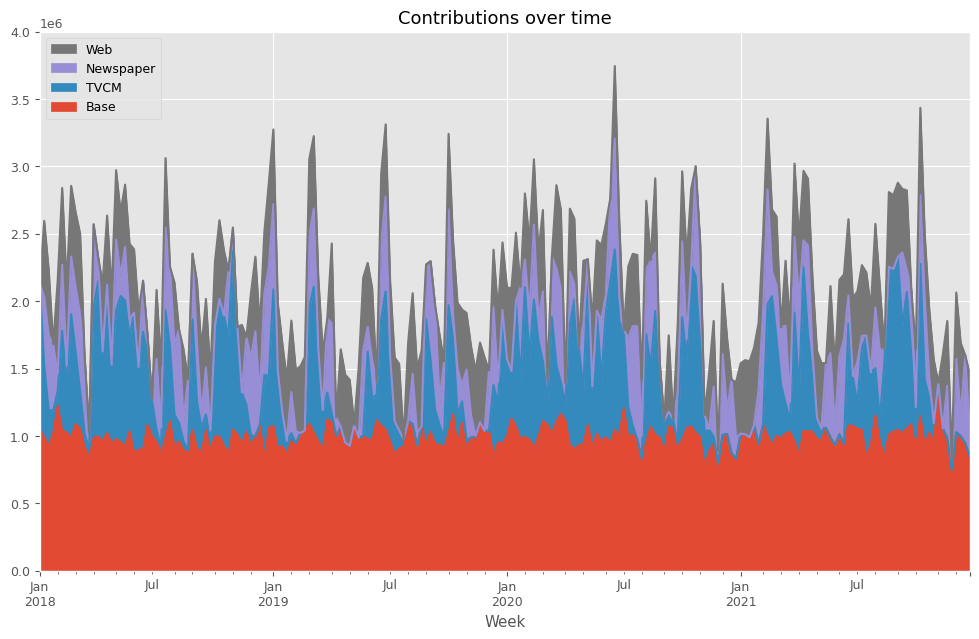
次に、貢献度の割合を計算します。

以下、コードです。

# 貢献度構成比の算出
contribution_results = summarize_and_plot_contribution(contribution)

 

以下、実行結果です。

           contribution     ratio
Base       2.060909e+08  0.469930
TVCM       9.009612e+07  0.205438
Newspaper  6.091943e+07  0.138909
Web        8.144970e+07  0.185722

 

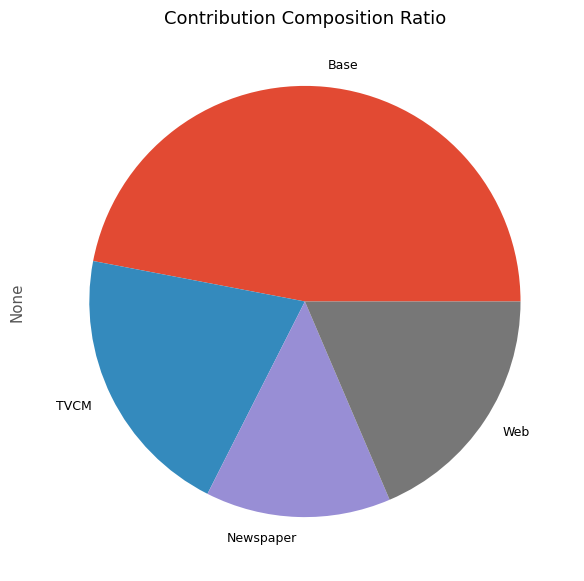
最後に、各メディアのマーケティングROIを計算します。

以下、コードです。

# マーケティングROIの算出
ROI = calculate_marketing_roi(X, contribution)

 

以下、実行結果です。

TVCM         0.549441
Newspaper    0.324733
Web          1.599793
dtype: float64 

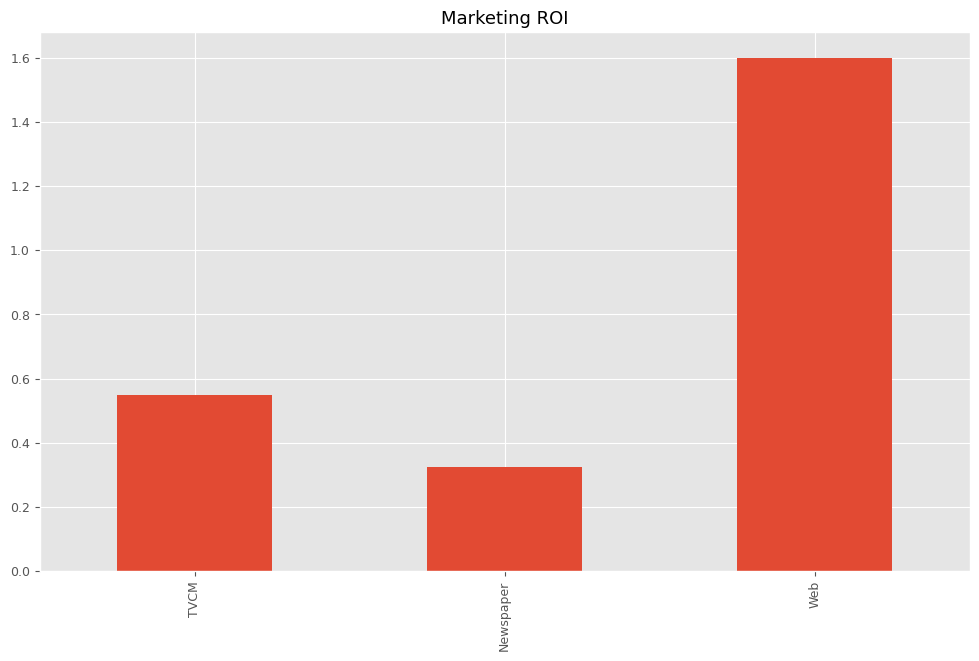
今まで構築したMMMの精度まとめ

今回の記事までに、いくつかの線形系のMMMが登場しました。詳細は以下の記事を一読ください。

以下は、アドストックなしMMMです。

以下は、シンプルなアドストック付きMMMです。

以下は、ちょっと一般的なアドストック付きMMMです。

以下は、アドストック線形回帰系MMM（飽和関数自動選択）です。

で今回は、アドストック線形回帰系MMM（推定器自動選択）です。

以下で登場した線形系のMMMを含めた、MMMの精度の一覧表を最後提示します。

	精度	売上貢献度（構成比）
アドストックなしMMM	RMSE: 284668 MAE: 237679 MAPE: 0.12 R2: 0.74	Base: 0.62 TVCM: 0.10 Newspaper: 0.10 Web: 0.18
シンプルなアドストック付きMMM	RMSE: 175245 MAE: 141137 MAPE: 0.07 R2: 0.90	Base: 0.43 TVCM: 0.22 Newspaper: 0.14 Web: 0.21
ちょっと一般的なアドストック付きMMM	RMSE: 167412 MAE: 134921 MAPE: 0.07 R2: 0.91	Base: 0.46 TVCM: 0.21 Newspaper: 0.14 Web: 0.18
アドストック線形回帰系MMM（飽和関数自動選択）	RMSE: 164833 MAE: 132411 MAPE: 0.07 R2: 0.91	Base: 0.47 TVCM: 0.21 Newspaper: 0.14 Web: 0.18
アドストック線形回帰系MMM（推定器自動選択）	RMSE: 164512 MAE: 131671 MAPE: 0.07 R2: 0.91	Base: 0.47 TVCM: 0.21 Newspaper: 0.14 Web: 0.19

何かしらアドストックを適切に考慮した場合（要は、ハイパーパラメータチューニング実施）あたりから、それほど精度や結果に差異はありません。

まとめ

今回は、アドストックの飽和関数を自動選択し構築するMMMというお話しをしました。

今までは、すべての特徴量（説明変数）が、すべてアドストックを考慮すべき変数として扱っていました。

現実のMMMでは、すべての特徴量（説明変数）がアドストックを考慮すべき変数とは限りません。考慮すべきでない変数もあります。

例えば、メディア関連とは関係のないカレンダー情報を元にした特徴量（例：クリスマス変数、初売り初日変数などの○○の日）や、季節性を表現する三角関数特徴量（SinとCosで表現）などは、アドストックを考慮すべきでない変数かもしれません。

ただ、某ファストフードのチキンなどのように、クリスマスイブに急激に跳ね上がり、次の日のクリスマスまで売上が高い場合には、キャリーオーバー効果（期間が2日間でピークが1日目）を考慮した方がいい場合もあります。

要するに、各特徴量（説明変数）の特性に応じて、ＭＭＭを構築するときに「アドストックを考慮すべき or アドストックを考慮すべきでない」を選べるといいでしょう。

ということで、次回は「アドストックを考慮すべき特徴量を指定し構築する線形回帰系ＭＭＭ」というお話しをします。

ＭＭＭパイプラインを、「アドストックを考慮すべき or アドストックを考慮すべきでない」で分岐する感じになります。

PythonによるMMM（マーケティングミックスモデリング）とビジネス活用－ 振返り分析・線形回帰系モデル編（その6）－線形回帰系ＭＭＭ（アドストック対象の特徴量を指定）