データを活用したマーケティング戦略は、ビジネスの成功に不可欠です。その中心に位置するのが、マーケティングミックスモデリング(MMM)です。
マーケティングミックスモデリング(MMM)は、過去のデータを分析する「振り返り分析」と未来のトレンドを予測する「近未来分析」の両方で有効に活用される強力なツールです。
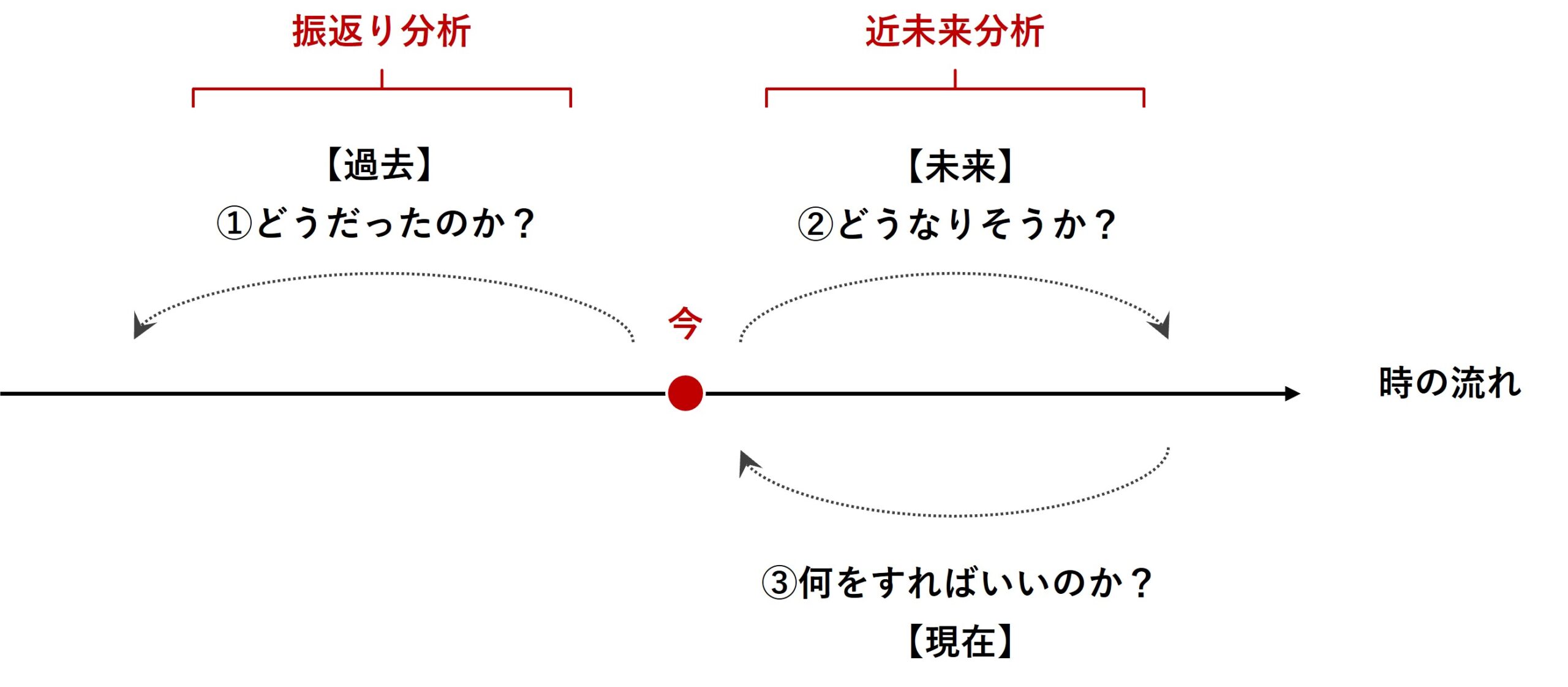
振返り分析のためのMMMは、各広告・販促の手段が、どのくらいの売上などに貢献し、それが効率的だったのかどうかを、明らかにすることでした。
さらに一歩先に話しを進め、どの広告・販促の手段に、どの程度のコストをかけて投資をするのが効率的なのか? を明らかにする振返り分析もあります。
要するに、広告・販促の手段にかけるコストの最適投資配分です。
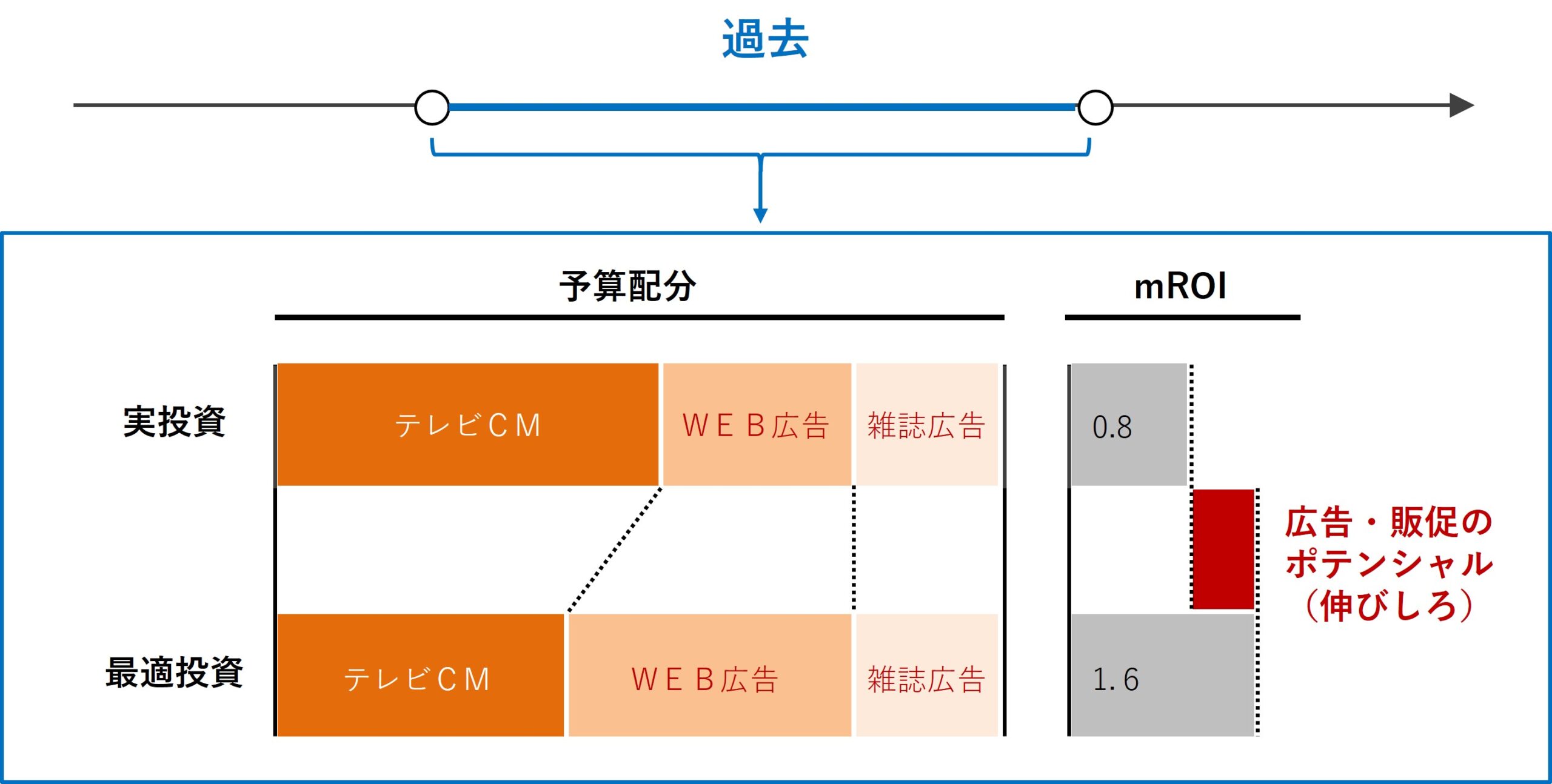
色々なアプローチがありますが、ストレートなのは非線形計画問題(非線形最適化)を定式化しソルバーで解くことです。具体的に言うと、PythonのScyPyである程度は実現することができます。
前回は、以下のRidge回帰ベースのアドストック付きMMM(Ridge MMMパイプライン)で、最適投資配分を求める方法をお話ししました。
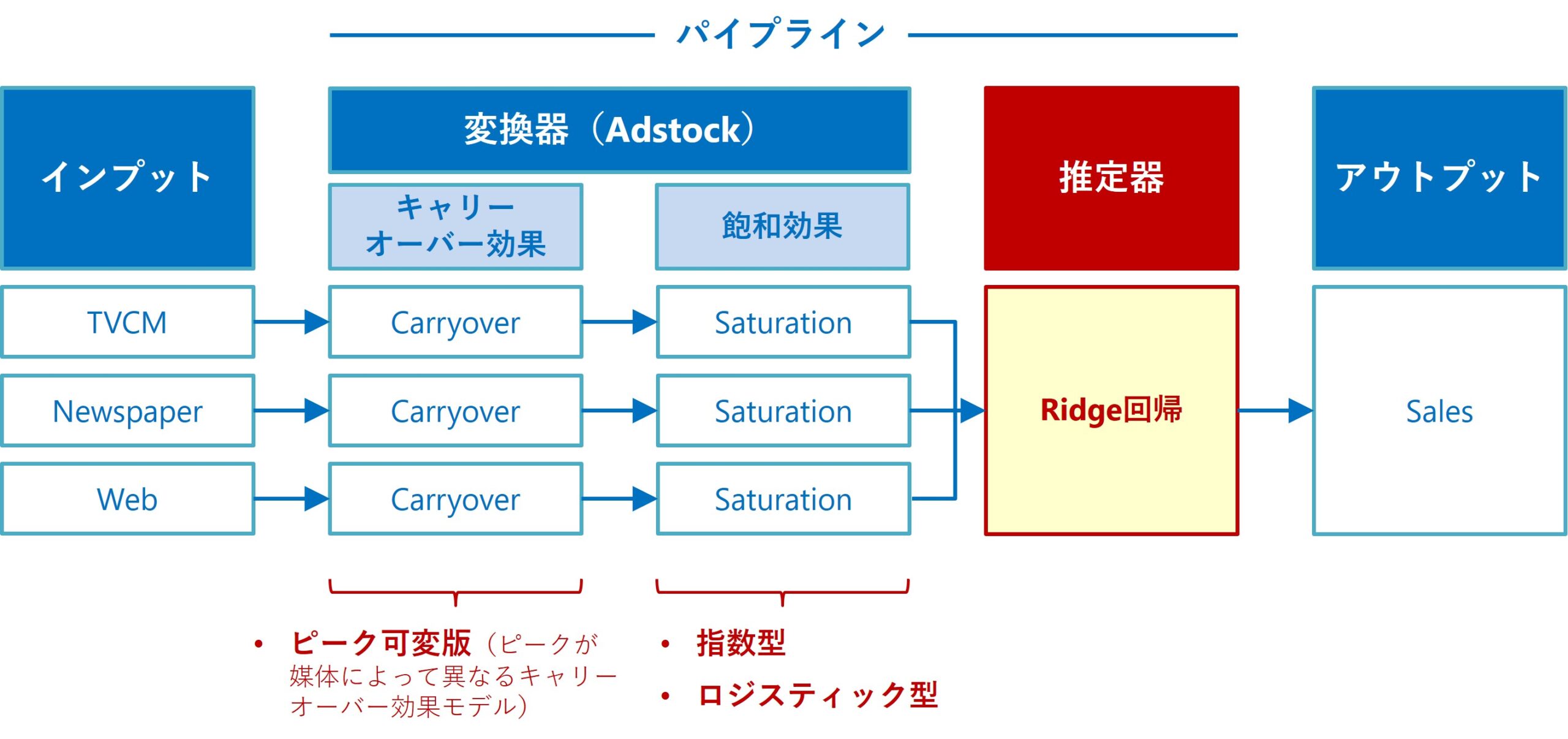
具体的には、全体コスト一定のもとで売上を最大化する非線形計画問題を解きました。
興味のある方は、前回の記事をご覧ください。
前回の記事では、特徴量(説明変数)Xのすべてが、アドストックを考慮し最適化すべきデータとしました。
しかし現実は、特徴量(説明変数)Xのすべてが、アドストックを考慮し最適化すべき広告・販促コストのデータでないかもしれません。
例えば、カレンダー情報を元にした特徴量(例:クリスマス変数、初売り初日変数などの○○の日)や、季節性を表現する三角関数特徴量(SinとCosで表現)などは、アドストックを考慮すべきでないかもしれませんし、最適化対象となるコストデータでもありません。
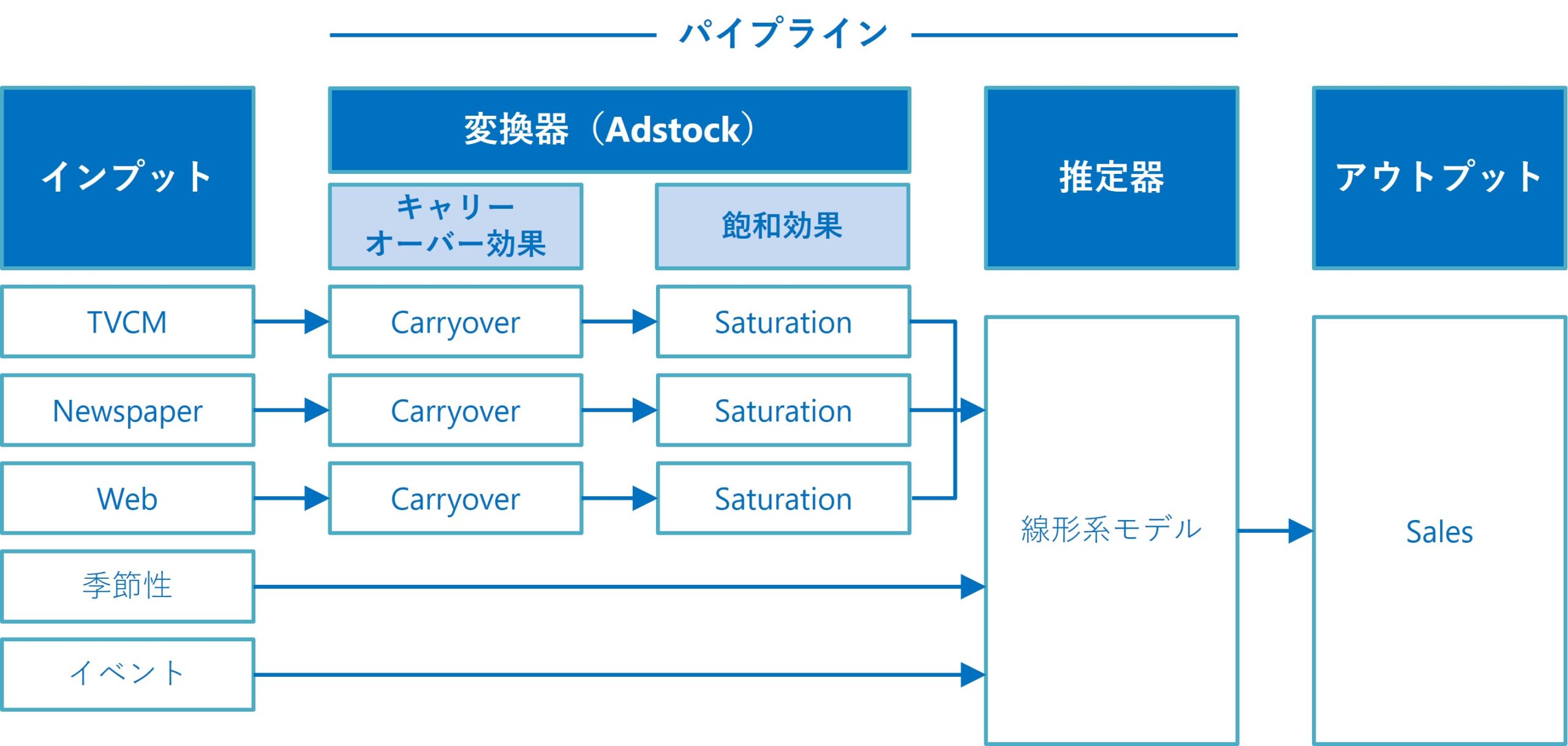
要するに、各特徴量(説明変数)の特性に応じて、MMMを構築するときに「アドストックを考慮すべき or アドストックを考慮すべきでない」、「最適化対象となるコストデータ or そうではない」を選べるといいでしょう。
ということで、今回は「アドストックを考慮すべきどうか、コスト最適化の対象かどうか、特徴量を指定し構築する線形回帰系MMM」というお話しをします。
Contents [hide]
利用するデータセット
以下のデータセットを利用します。
- 目的変数:売上金額(Sales)
- 説明変数:
- メディア:TVCM、Newspaper、Webのコスト
- イベント:XMas(クリスマス)フラグ(1: 12月25日、0: その他)
今回利用するデータセットは、以下からダウンロードできます。
MMM_xmas.csv
https://www.salesanalytics.co.jp/dcbd
今回は、以下のように設定しました。
- アドストックを考慮する:TVCM、Newspaper、Webのコスト
- アドストックを考慮しない:XMas(クリスマス)フラグ(1: 12月25日、0: その他)
今回構築するMMMと最適化
今回のMMM(マーケティングミックスモデリング)の予算最適化問題は、全体コスト一定の下で売上を最大化する、広告・販促の手段に対するコストの最適配分を求める問題になります。

MMMそのものが目的関数、MMMの出力である売上が目的変数になります。
今回構築するMMMは、人がハイパーパラメータを付与するRidge MMMパイプラインです。
特徴量は2つの視点で分けていきます。
- アドストックを考慮すべき特徴量 or そうでない特徴量
- アドストックを考慮する:TVCM、Newspaper、Webのコスト
- アドストックを考慮しない:XMas(クリスマス)フラグ(1: 12月25日、0: その他)
- 最適化対象となる特徴量 or そうではない特徴量
今回のケースですと、アドストックを考慮すべき特徴量=最適化対象となる特徴量ですが、必ずしもそうではありません。
そこで今回は、最適化対象となる特徴量を以下の3パターンを想定します。
- パターン1:TVCM、Newspaper、Webのコストを最適化
- パターン2:Newspaper、Webのコストを最適化
- パターン3:TVCMのコストのみ最適化
準備
モジュールの読み込み
先ず、必要なモジュールを読み込みます。
以下、コードです。
from mmm_functions5 import *
Pythonファイル(mmm_functions5.py)そのものは、以下からダウンロードできます。
mmm_functions5.py ※zipファイルを解凍してお使いください
https://www.salesanalytics.co.jp/uno8
mmm_functions5.pyには、MMMで共通して利用する処理を関数化したものや、クラス、モジュール類などを記載しています。
mmm_functions5.pyを利用するときは、実行するPythonファイルやNotebookと同じフォルダに入れておいてください。
上手くいかないときは、mmm_functions5.pyをメモ帳などで開き内容をコピーし、実行するPythonファイルやNotebookにコードを張り付け、Pythonで関数を作ってからMMM構築などを行ってください。
データセットの読み込み
以下、コードです。
# データセット読み込み
dataset = 'https://www.salesanalytics.co.jp/dcbd'
df = pd.read_csv(
dataset,
parse_dates=['Week'],
index_col='Week',
)
# 説明変数Xと目的変数yに分解
X = df.drop(columns=['Sales'])
y = df['Sales']
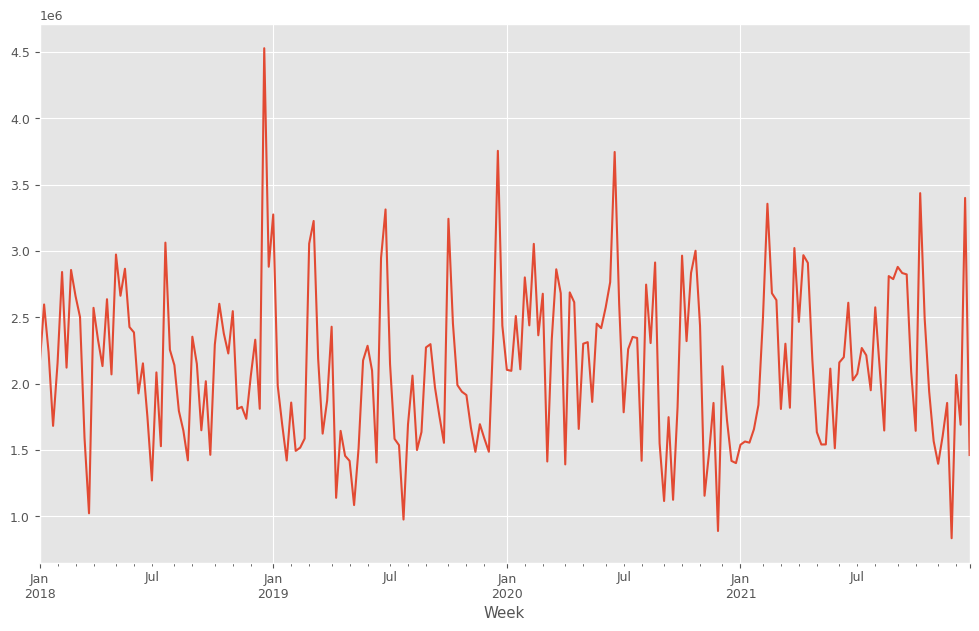
目的変数y(売上)をプロットします。
以下、コードです。
y.plot() plt.show()
以下、実行結果です。

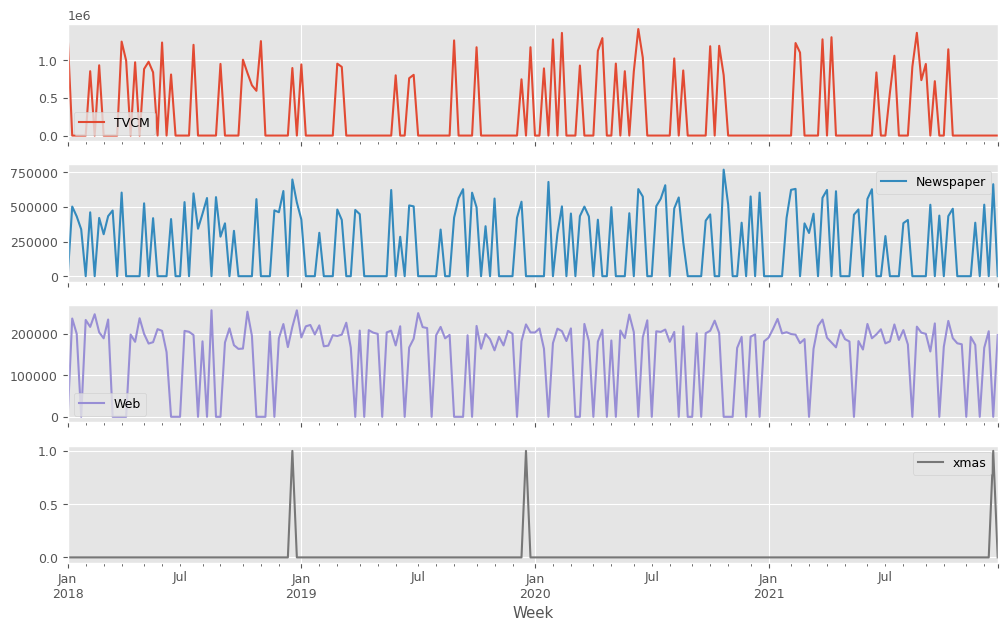
説明変数X(各メディアのコスト)をまとめてプロットします。
以下、コードです。
X.plot(subplots=True,figsize=(12,X.shape[1]*3)) plt.show()
以下、実行結果です。XMas変数は0-1変数(12月25日に1、その他の日は0)で、他の変数はコストデータです。

目的関数作り
今回の最適投資配分問題の目的関数は、Ridge MMMMパイプラインそのものになります。
ハイパーパラメータの設定
Ridge MMMパイプラインのハイパーパラメータを設定します。
以下、コードです。
# 各特徴量に対するキャリーオーバー効果のパラメータ設定
carryover_params = [
{'length': 6,'peak': 1,'rate1': 0.3,'rate2': 0.5,'c1': 0.4,'c2': 0.5},
{'length': 3,'peak': 1,'rate1': 0.6,'rate2': 0.5,'c1': 1.1,'c2':1.6},
{'length': 4,'peak': 2,'rate1': 0.9,'rate2': 0.2,'c1': 1.7,'c2': 1.1},
]
# 各特徴量に対する飽和関数のパラメータ設定
curve_params = [
{'saturation_function': 'logistic','L': 9.8,'k': 9.1,'x0': 0.14},
{'saturation_function': 'exponential', 'd': 5},
{'saturation_function': 'logistic','L': 3.6,'k': 4,'x0': 0.6},
]
# 特徴量名の設定
feature_names = apply_effects_features
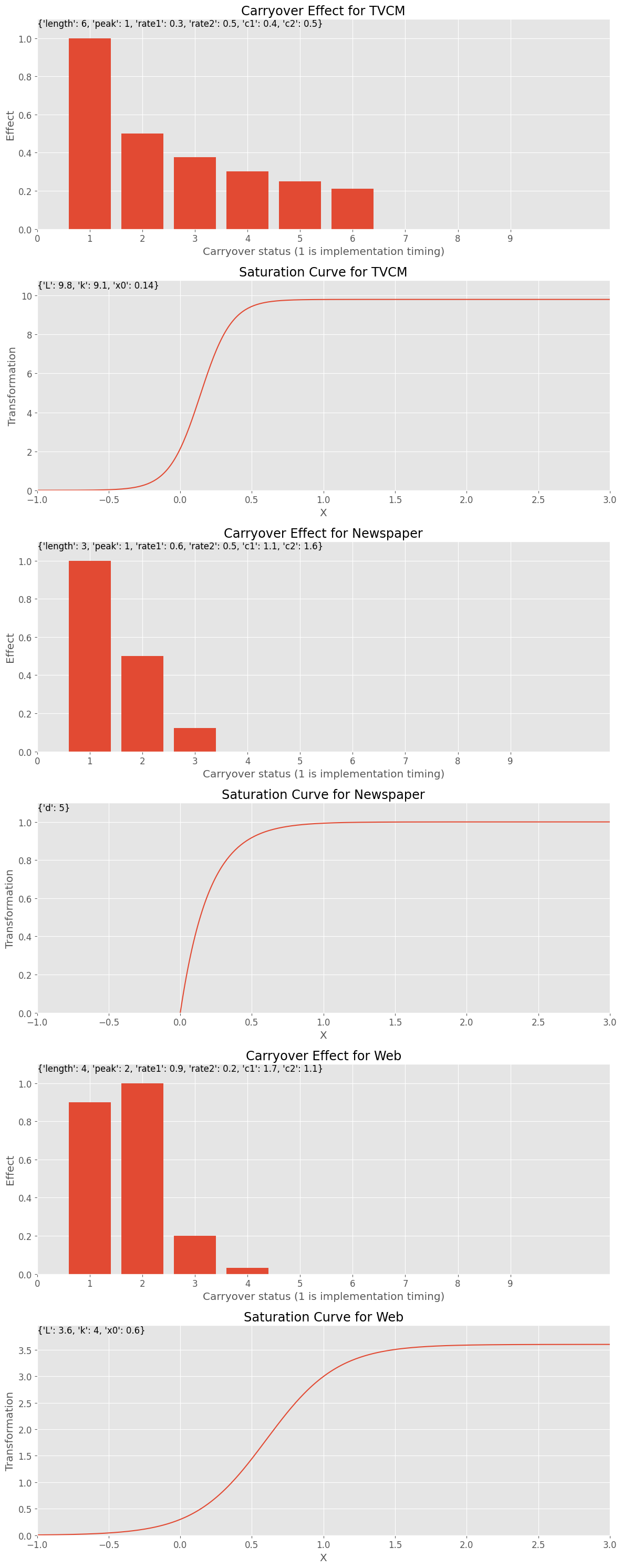
# グラフで確認
plot_effects(carryover_params, curve_params, feature_names)
以下、実行結果です。
MMMパイプラインの構築
先ず、アドストックを考慮する特徴量のリストを作ります。
以下、コードです。
# アドストックを考慮する特徴量のリストを作成 apply_effects_features = ['TVCM', 'Newspaper', 'Web']
MMMパイプラインを構築します。
以下、コードです。
# 列名リストからインデックスのリストを作成
apply_effects_indices = [X.columns.get_loc(column) for column in apply_effects_features]
no_effects_indices = list(set(range(X.shape[1])) - set(apply_effects_indices))
# ColumnTransformerを使って特定の列にのみアドストックの変換を適用する
preprocessor = ColumnTransformer(
transformers=[
('effects', Pipeline([
('carryover_transformer', CustomCarryOverTransformer(carryover_params=carryover_params)),
('saturation_transformer', CustomSaturationTransformer(curve_params=curve_params))
]), apply_effects_indices),
('no_effects', 'passthrough', no_effects_indices)
],
remainder='drop' # 効果適用外の特徴量は処理しない
)
# パイプラインの構築
MMM_pipeline = Pipeline([
('scaler', MinMaxScaler()),
('preprocessor', preprocessor),
('estimator', Ridge())
])
# パイプラインを使って学習
trained_model, pred = train_and_evaluate_model(MMM_pipeline, X, y)
以下、実行結果です。
RMSE: 296340.3031890805 MAE: 238849.91174925564 MAPE: 0.12512848085904074 R2: 0.7546773035954673
RMSE (Root Mean Squared Error): 296340
この値は平均二乗誤差の平方根を表しており、予測値と実際値の差の大きさを示します。値が小さいほど良いモデルということになります。
MAE (Mean Absolute Error): 238850
これは絶対誤差の平均値で、予測値と実際値の差の絶対値の平均を表します。値が小さいほど良いモデルです。
MAPE (Mean Absolute Percentage Error): 0.1251(12.51%)
この指標はパーセンテージで表された絶対誤差の平均値です。100%に近づくほど予測精度が低くなります。
R2 (R-squared): 0.7547 (75.47%)
決定係数と呼ばれ、モデルの当てはまり具合を0から1の範囲で表します。1に近いほど当てはまりが良いことを意味します。
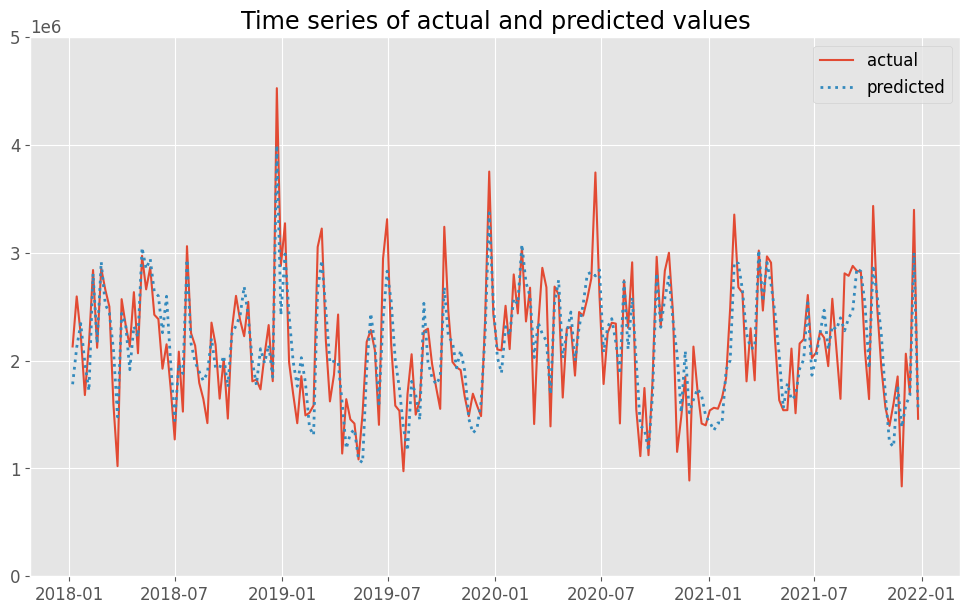
実測値と予測値の時系列推移を比較してみます。
以下、コードです。
# 実測値と予測値の時系列推移 plot_actual_vs_predicted(y.index, y.values, pred.y.values, (0, 5e6))
以下、実行結果です。actualが実測値で、predictedが予測値です。
(必要があれば)学習済みモデルの保存と読み込み
必要があれば、学習済みのMMMパイプラインを外部ファイル(joblib形式)として保存しておくといいでしょう。
以下、コードです。
# 学習済みモデルtrained_modelを外部ファイルとして保存する model_path = 'ridgeMMM_trained_model.joblib' joblib.dump(trained_model, model_path)
外部ファイル(joblib形式)として保存した学習済みのMMMパイプラインを読み込むとき、以下のコードで実施します。
以下、コードです。
# 外部ファイル(学習済みモデル)を読み込む model_path = 'ridgeMMM_trained_model.joblib' trained_model = joblib.load(model_path)
売上貢献度とマーケティングROI
このMMMパイプラインから、売上貢献度やマーケティングROIなどを求めていきます。
先ずは、貢献度の推移です。
以下、コードです。
# 貢献度の算出 contribution = calculate_and_plot_contribution(y, X, trained_model,(0, 5e6)) print(contribution)
以下、実行結果です。
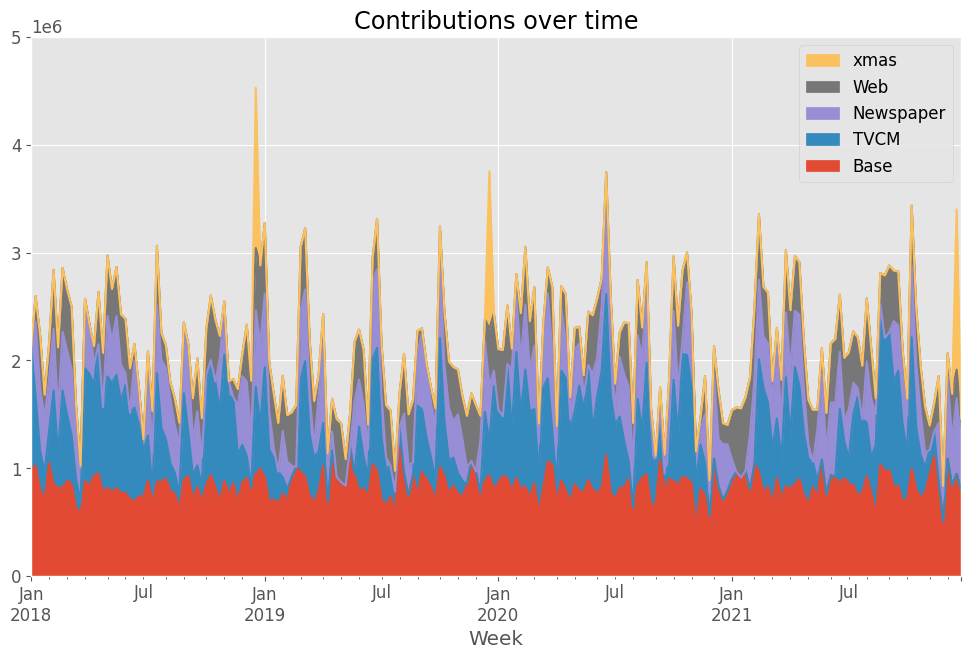
Base TVCM Newspaper Web \
Week
2018-01-07 1.000697e+06 1.131303e+06 0.000000 0.000000
2018-01-14 1.022413e+06 6.407488e+05 693227.728751 239710.358369
2018-01-21 7.975337e+05 3.631155e+05 583636.510512 491914.299864
2018-01-28 7.111474e+05 2.515021e+05 509220.782804 209029.693254
2018-02-04 1.046806e+06 2.990721e+05 482464.229379 327057.885593
... ... ... ... ...
2021-11-28 5.042975e+05 0.000000e+00 212530.277864 117072.212187
2021-12-05 1.087274e+06 0.000000e+00 761830.249135 215595.459216
2021-12-12 8.406574e+05 0.000000e+00 424028.209569 424814.410744
2021-12-19 9.472107e+05 0.000000e+00 700945.247936 264697.671783
2021-12-26 7.992093e+05 0.000000e+00 460049.827620 201840.887008
xmas
Week
2018-01-07 0.000000e+00
2018-01-14 0.000000e+00
2018-01-21 0.000000e+00
2018-01-28 0.000000e+00
2018-02-04 0.000000e+00
... ...
2021-11-28 0.000000e+00
2021-12-05 0.000000e+00
2021-12-12 0.000000e+00
2021-12-19 1.486346e+06
2021-12-26 0.000000e+00
[208 rows x 5 columns]
次に、貢献度の構成比を求めます。
以下、コードです。
# 貢献度構成比の算出 contribution_results = summarize_and_plot_contribution(contribution) print(contribution_results)
以下、実行結果です。
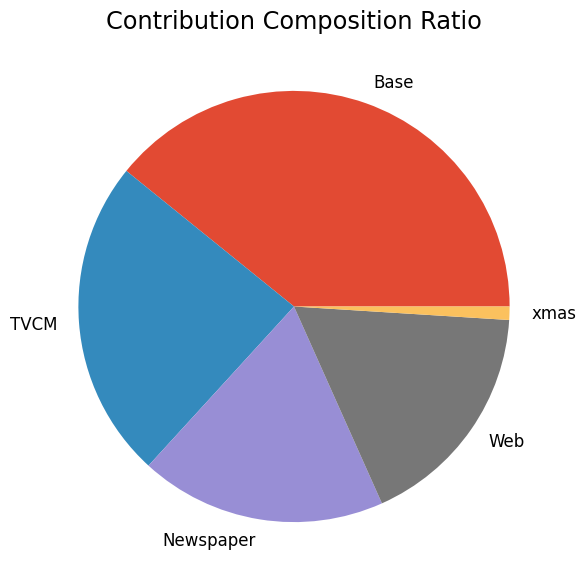
contribution ratio Base 1.740112e+08 0.391744 TVCM 1.067782e+08 0.240385 Newspaper 8.206516e+07 0.184750 Web 7.690863e+07 0.173141 xmas 4.433500e+06 0.009981
売上貢献度とコストから、マーケティングROIを求めます。
以下、コードです。
# マーケティングROIの算出
ROI = calculate_marketing_roi(
X[apply_effects_features],
contribution[apply_effects_features]
)
# 数値を表示
print(ROI)
以下、実行結果です。
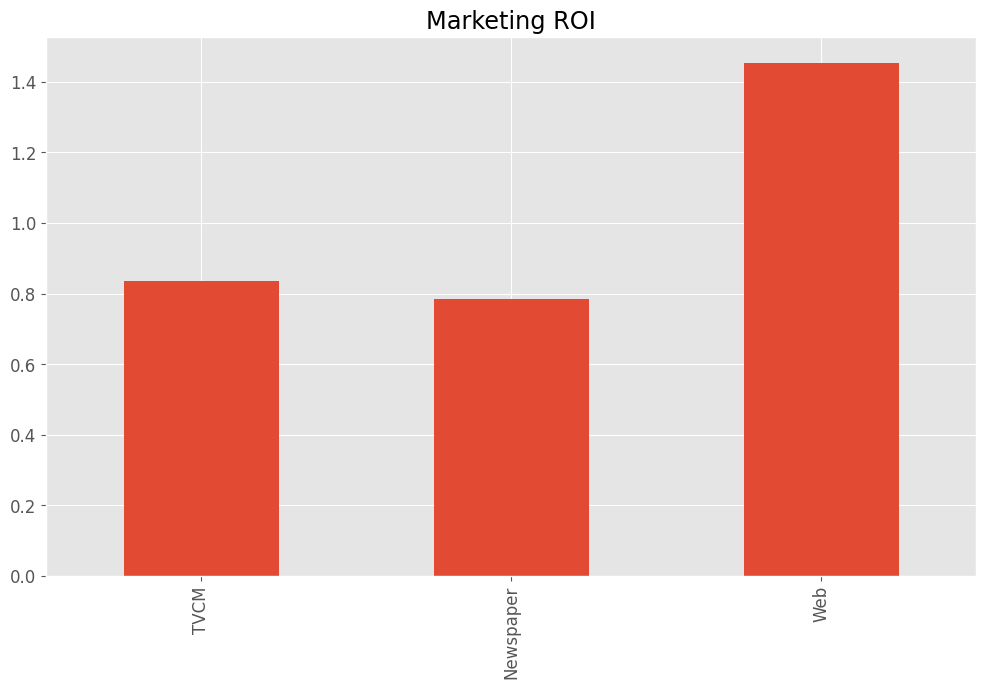
TVCM 0.836334 Newspaper 0.784561 Web 1.454847 dtype: float64
売上貢献度(横軸)×マーケティングROI(縦軸)のマップを描きます。円の大きさはコストを表します。
以下、コードです。
# 散布図作成(売上貢献度×マーケティングROI)
data_to_plot = plot_scatter_of_contribution_and_roi(
X[apply_effects_features],
contribution[apply_effects_features]
)
# 散布図の数値を表示
print(data_to_plot)
以下、実行結果です。
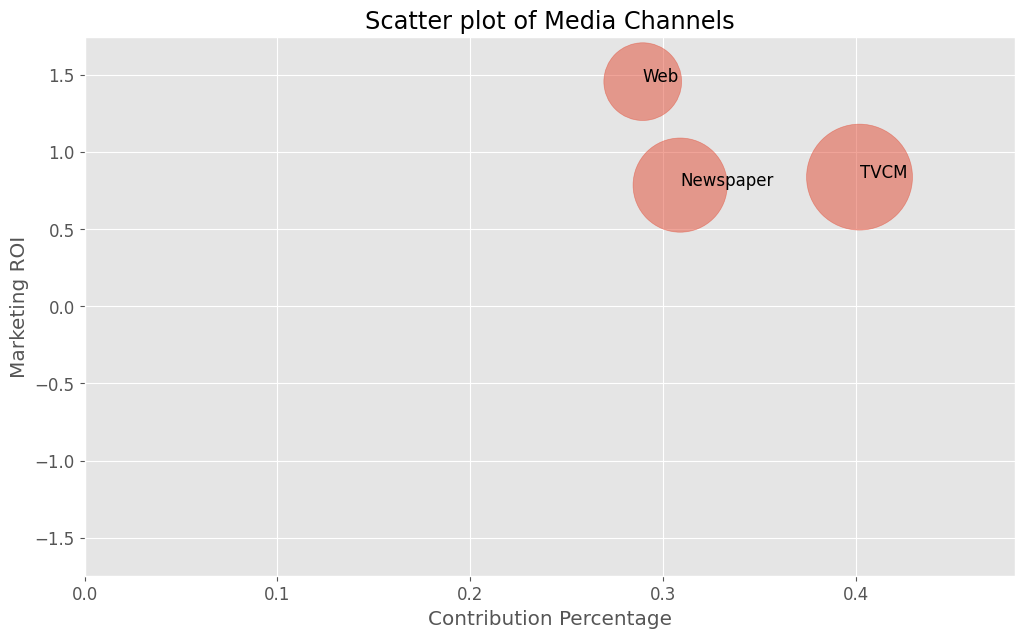
contribution_percentage ROI cost TVCM 0.401796 0.836334 58147500 Newspaper 0.308804 0.784561 45986200 Web 0.289400 1.454847 31329300
最適投資配分
構築したRidge MMMMパイプラインを最大化する最適投資配分問題を解き、広告・販促のコストの最適投資配分を求めます。
最後に、現状と最適化後の結果を比較し、どのような変化が起こるかを出力します。
関数の定義
最適投資配分を求める関数を作ります。
この関数でScyPyで、MMMパイプラインの出力である売上を全体コスト一定(現在のコストを合計した値)のもとで最大化する、非線形最適問題を定義し、最適解を求めます。
以下、コードです。
#
# 最適投資配分
#
def optimize_investment(trained_model, X_actual, optimized_features, niter = 100):
"""
与えられた機械学習モデルと特徴量のデータフレームを受け取り、最適な広告出稿配分を算出する。
引数:
- trained_model: 学習済みの機械学習モデル
- X_actual: 特徴量のデータフレーム
- optimized_features: 最適化対象の特徴量(アドストックを考慮しない特徴量)
- niter: int, 最適化プロセスにおける反復回数。デフォルトは100
戻り値:
- opt_results: {
'optimizeResult': 最適化の結果
'X_optimized': 最適化期間における対象特徴量のデータフレーム
}
"""
# 最適化する期間
term = X_actual.shape[0]
# プログレスバーを表示するための関数
def callback(xk, f, accept):
progression.update(1)
# プログレスバーを表示するためのインスタンス
progression = tqdm.tqdm(
total=niter, position=0, leave=True)
# 最適化期間における対象特徴量のデータを抽出
X_before = X_actual[optimized_features].copy()
# 最適化期間における対象外特徴量のデータを抽出
X_no_effects = X_actual.drop(optimized_features, axis=1).copy()
# 目的関数の定義
def objective_function(x):
# xをデータフレームに変換
x_pd = pd.DataFrame(
x.reshape(term, len(X_before.columns)),
index=X_before.index,
columns=X_before.columns)
# 最適化対象外の特徴量との結合
x_combined = pd.concat(
[x_pd, X_no_effects],
axis=1)
x_combined = x_combined[X_actual.columns]
# 予測値の計算
pred_value = trained_model.predict(x_combined)
# 目的関数の値(予測値の和の負値)を返す
return -1 * pred_value.sum()
# 元の総投資額の計算
cost_all = X_before.values.ravel().sum()
# 制約条件の定義:総投資額が同じになるように
constraint = {"type":"eq","fun": lambda x: cost_all-x.sum()}
# 投資額の上限と下限の定義
lower = [0] * X_before.size
upper = [np.inf] * X_before.size
# minimizer_kwargsの設定
minimizer_kwargs = dict(
method="SLSQP",
bounds=Bounds(lower, upper),
constraints=(constraint))
# 初期解の設定
x_0 = X_before.values.ravel()
# 初期解の目的関数値の合計の負値
init_obj_value = -1 * objective_function(x_0)
# 目的関数の再定義(初期解より改善)
def revised_objective_function(x):
obj_value = objective_function(x)
return obj_value if obj_value < init_obj_value else 0
# 最適化の実行
optimizeResult = basinhopping(
revised_objective_function,
x_0,
minimizer_kwargs=minimizer_kwargs,
niter=niter,
T=10,
stepsize=100000,
seed=0,
callback=callback)
# プログレスバーを閉じる
progression.close()
# 最適解と最適化対象外の特徴量を結合
x_pd = pd.DataFrame(
optimizeResult.x.reshape(term, len(X_before.columns)),
index=X_before.index,
columns=X_before.columns)
X_optimized = pd.concat(
[x_pd, X_no_effects],
axis=1)
X_optimized = X_optimized[X_actual.columns]
# 最適化の結果を返す
opt_results = {
'optimizeResult':optimizeResult,
'X_optimized':X_optimized
}
return opt_results
得た最適解から、最適化前後の目的変数yとマーケティングROIを比較するグラフを作成する関数を作ります。
以下、コードです。
def compare_y_and_marketing_roi(X_optimized, X_actual, y_actual, trained_model, apply_effects_features):
"""
現状と最適配分時のyおよびマーケティングROIを比較し、結果をグラフとして表示します。
戻り値として、実測値と最適配分時のパラメータ(yの合計とマーケティングROI)を含む辞書を返します。
引数:
- X_optimized (pd.DataFrame): 最適化後の特徴量
- X_actual (pd.DataFrame): 実測値の特徴量
- y_actual (pd.Series): 実測値のターゲット変数
- trained_model: 学習済みの機械学習モデル
- apply_effects_features (list): 適用する特徴量のリスト
戻り値:
- dict: {
'y_actual': 実測値のyの合計,
'y_optimized': 最適配分時のyの合計,
'y_change_percent': yの変化率(パーセント),
'roi_actual': 実測値のマーケティングROI,
'roi_optimized': 最適配分時のマーケティングROI,
'roi_change_point': ROIの変化ポイント
}
"""
# 元の総投資額の計算
cost_all = X_actual[apply_effects_features].sum().sum()
# yの実測値の合計
y_actual_sum = round(y_actual.sum())
# 修正比率の計算(実測のyと予測の比)
correction_ratio = y_actual.sum()/trained_model.predict(X_actual).sum()
# 最適配分時のyの合計
pred = trained_model.predict(X_optimized)
y_optimized_sum = round(pred.sum()*correction_ratio)
# yの変化率の計算
y_change_percent = ((y_optimized_sum - y_actual_sum) / y_actual_sum) * 100
# yの変化率の符号
sign_y = '+' if y_change_percent >= 0 else '-'
# 現状のマーケティングROI
roi_actual = ((y_actual_sum - cost_all) / cost_all)
# 最適配分時のマーケティングROI
roi_optimized = ((y_optimized_sum - cost_all) / cost_all)
# roiの変化ポイントの計算
roi_change_point = roi_optimized - roi_actual
# roiの変化の符号
sign_roi = '+' if roi_change_point >= 0 else '-'
# グラフのFigure
fig, axs = plt.subplots(2, 1, figsize=(12,14))
labels = ['Actual', 'Optimized']
y_values = [y_actual_sum, y_optimized_sum]
roi_values = [roi_actual, roi_optimized]
axs[0].bar(labels, y_values, color=['blue', 'orange'])
axs[0].set_title('Comparison of y: Actual vs. Optimized')
axs[0].set_ylabel('y')
for i, value in enumerate(y_values):
axs[0].text(i, value, f'{int(value)}', ha='center', va='bottom')
axs[1].bar(labels, roi_values, color=['blue', 'orange'])
axs[1].set_title('Comparison of Marketing ROI: Actual vs. Optimized')
axs[1].set_ylabel('ROI')
for i, value in enumerate(roi_values):
axs[1].text(i, value, f'{value:.2f}', ha='center', va='bottom')
plt.tight_layout()
plt.show()
return {
'y_actual_sum': f"{y_actual_sum}",
'y_optimized_sum': f"{y_optimized_sum}",
'y_change_percent': f"{sign_y}{abs(y_change_percent):.2f} %",
'roi_actual': f"{roi_actual:.2f}",
'roi_optimized': f"{roi_optimized:.2f}",
'roi_change_point': f"{sign_roi}{abs(roi_change_point):.2f} points"
}
さらに、最適化前後の投資配分構成比を比較するグラフを作成する関数を作ります。
以下、コードです。
#
# 投資配分構成比の比較
#
def plot_comparative_allocation(X_actual, X_optimized, apply_effects_features):
"""
最適化前と最適化後のメディアコスト配分の構成比を比較し、グラフで表示する関数。
引数:
- X_actual (pd.DataFrame): 実測値の特徴量
- X_optimized (pd.DataFrame): 最適化後の特徴量
- apply_effects_features (list): 適用する特徴量のリスト(コストデータの特徴量)
戻り値:
- comparison_df (pd.DataFrame): 最適化前と最適化後のメディアコストの割合を比較したDataFrame
"""
# 最適化前(実投資)の構成比
X_before = X_actual[apply_effects_features]
X_before_ratio = X_before.sum()/X_before.sum().sum()
# 最適投資の構成比
X_after = X_optimized[apply_effects_features]
X_after_ratio = X_after.sum()/X_after.sum().sum()
# 構成比の表示
comparison_df = pd.DataFrame({
'Actual Allocation': X_before_ratio,
'Optimized Allocation': X_after_ratio})
# グラフ化
fig, ax = plt.subplots()
bottom = np.zeros(2)
for value, feature in zip(comparison_df.values, apply_effects_features):
ax.bar(['Actual', 'Optimized'], value, bottom=bottom, label=feature)
bottom += value
ax.set_title('Media Cost Allocation')
ax.set_ylabel('% of Total Investment')
handles, labels = ax.get_legend_handles_labels()
ax.legend(handles[::-1], labels[::-1])
ax.set_ylim([0, 1])
plt.show()
return comparison_df
最適化する期間の設定
最適化する期間は、直近1年間(52週間)です。
以下、コードです。
# 最適化期間を表す変数、ここでは直近1年間(52週間)を指定 term = 52 # 最適化期間における対象特徴量Xのデータを抽出 X_actual = X[-term:] # 最適化期間における目的変数yのデータを抽出 y_actual = y[-term:]
今回は、最適化対象となる特徴量を以下の3パターンを想定します。
- パターン1:TVCM、Newspaper、Webのコストを最適化
- パターン2:Newspaper、Webのコストを最適化
- パターン3:TVCMのコストのみ最適化
パターン1:TVCM、Newspaper、Webのコストを最適化
以下を最適対象の特徴量とします。
- TVCM:最適対象の特徴量
- Newspaper:最適対象の特徴量
- Web:最適対象の特徴量
以下、コードです。
# 最適化対象の特徴量のリストを作成 optimized_features = ['TVCM', 'Newspaper', 'Web']
最適化の実行
MMMパイプラインの出力である売上を全体コスト一定(現在のコストを合計した値)のもとで最大化する、非線形最適問題を定義し、最適解を求めます。
以下、コードです。
#
# 最適投資配分
#
opt_results = optimize_investment(
trained_model,
X_actual,
optimized_features,
niter = 100)
最適化の計算が終了したら、その最適解を取得します。
以下、コードです。
# # 最適解の取得 # X_optimized = opt_results['X_optimized'] # 最適化後の特徴量を表示 print(X_optimized)
以下、実行結果です。
TVCM Newspaper Web xmas Week 2021-01-03 48822.155766 162744.939172 558825.681376 0 2021-01-10 89474.518603 93843.163352 35059.747456 0 2021-01-17 63989.581426 144468.205621 362479.445485 0 2021-01-24 76322.854172 132578.225222 151554.833214 0 2021-01-31 25907.534245 84588.507237 364965.225200 0 2021-02-07 4384.244413 122983.014991 103098.389581 0 2021-02-14 693313.061530 134556.200753 379582.416716 0 2021-02-21 607139.331796 99244.259060 160062.799588 0 2021-02-28 359760.955518 98699.385413 343008.653834 0 2021-03-07 307290.524642 113175.091038 96511.582833 0 2021-03-14 53914.963724 116356.430269 449288.679978 0 2021-03-21 152855.291496 134884.267527 75922.937172 0 2021-03-28 526883.377864 59692.703730 422576.960307 0 2021-04-04 184871.162901 178339.468874 76250.665524 0 2021-04-11 565649.674304 91457.563890 392726.457627 0 2021-04-18 376991.799753 158051.467089 211349.140857 0 2021-04-25 54677.554300 56107.983509 230397.871741 0 2021-05-02 177464.584827 113677.278767 243901.998086 0 2021-05-09 539182.332195 146580.195064 320704.808652 0 2021-05-16 211831.676640 102320.805496 161055.493242 0 2021-05-23 480962.128732 97696.099995 364256.932113 0 2021-05-30 347190.918875 125821.226952 185196.262757 0 2021-06-06 340798.008470 155832.214424 302962.694945 0 2021-06-13 235995.716465 102865.813607 195493.848319 0 2021-06-20 340360.136302 101020.998896 334891.489767 0 2021-06-27 223893.071187 119492.423242 160500.833358 0 2021-07-04 1143.858687 95646.473263 349708.989980 0 2021-07-11 650189.864423 150857.864203 196058.054476 0 2021-07-18 334788.750983 80337.630844 284779.595876 0 2021-07-25 441155.111330 97159.580902 283966.771679 0 2021-08-01 171469.481101 138363.735910 221776.301009 0 2021-08-08 162337.164684 81776.731953 303433.450419 0 2021-08-15 472527.665001 154246.914866 175486.287953 0 2021-08-22 384533.212741 56395.643833 298626.113120 0 2021-08-29 152135.994955 143263.332107 253624.393626 0 2021-09-05 349526.498829 130637.418161 174188.618891 0 2021-09-12 349249.552352 53596.286739 352489.840464 0 2021-09-19 320238.578045 163159.653961 166625.359009 0 2021-09-26 363334.218019 124009.649919 267528.595898 0 2021-10-03 251054.602929 110285.104517 274254.548325 0 2021-10-10 498453.116137 121763.040938 215807.084961 0 2021-10-17 185919.159841 103556.147827 249197.039498 0 2021-10-24 303594.291680 192493.665315 333780.656177 0 2021-10-31 428550.609435 84337.276672 187791.119454 0 2021-11-07 227531.513169 129045.902969 235956.537691 0 2021-11-14 411658.678072 71147.019890 298332.134361 0 2021-11-21 380952.059262 137565.198235 152430.549046 0 2021-11-28 170288.693732 111424.036305 350148.406220 0 2021-12-05 16642.708478 144776.779459 150857.806057 0 2021-12-12 1764.126760 85576.161319 348802.216453 0 2021-12-19 0.101121 132429.444734 324107.009255 1 2021-12-26 0.039796 111.888973 9.341658 0
最適投資配分の最適化結果の出力
現状と最適化の結果を比較していきます。
先ずは、売上金額とマーケティングROIです。
以下、コードです。
#
# 現状と最適配分時の比較(yとマーケティングROI)
#
result = compare_y_and_marketing_roi(
X_optimized,
X_actual,
y_actual,
trained_model,
apply_effects_features)
# 数値の表示
for key,value in result.items():
print(f"{key}: {value}")
以下、実行結果です。
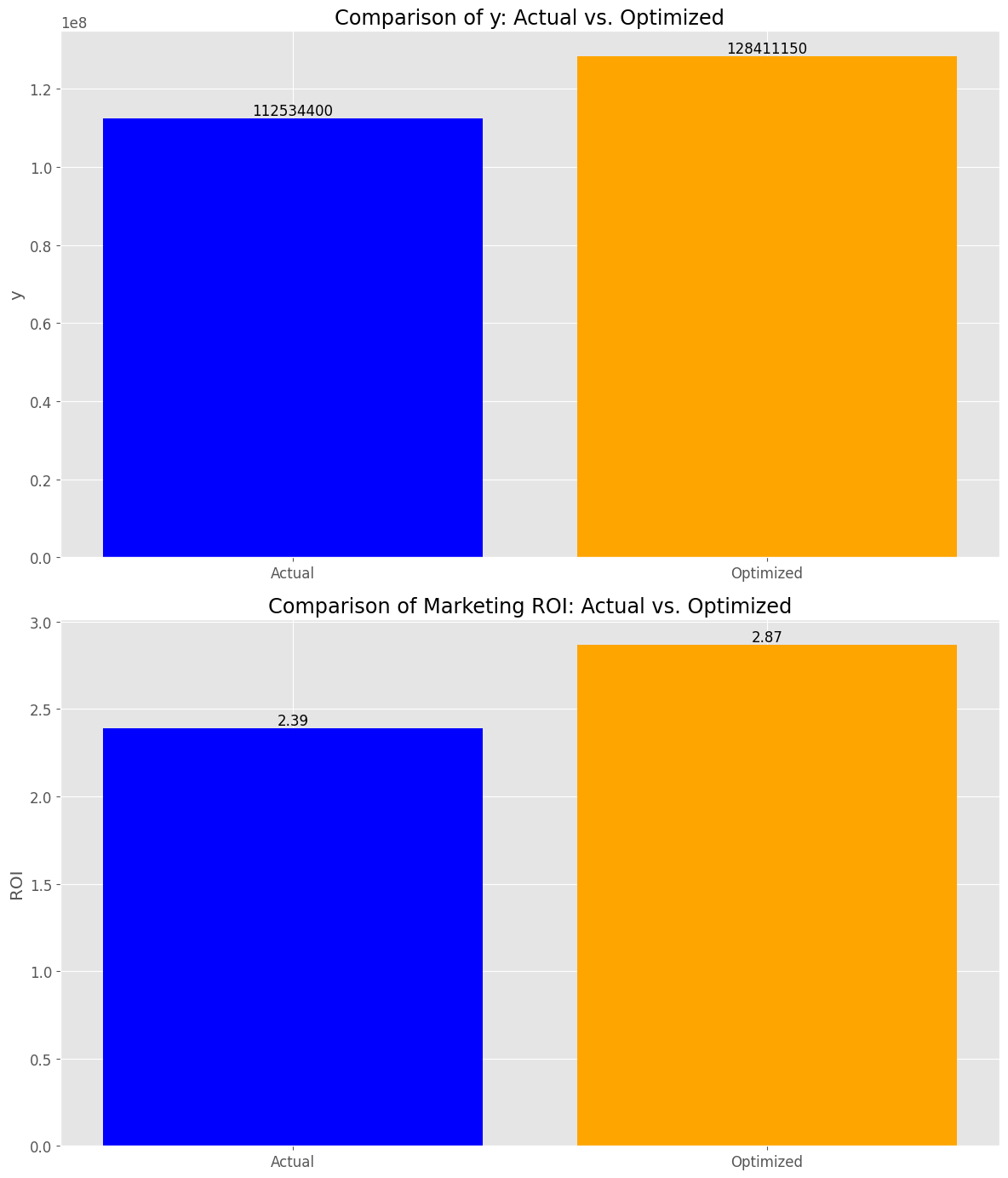
y_actual_sum: 112534400 y_optimized_sum: 128411150 y_change_percent: +14.11 % roi_actual: 2.39 roi_optimized: 2.87 roi_change_point: +0.48 points
次に、投資配分です。
以下、コードです。
#
# 投資配分構成比の比較
#
comparison_df = plot_comparative_allocation(
X_actual,
X_optimized,
apply_effects_features)
# 数値の表示
print(comparison_df)
以下、実行結果です。
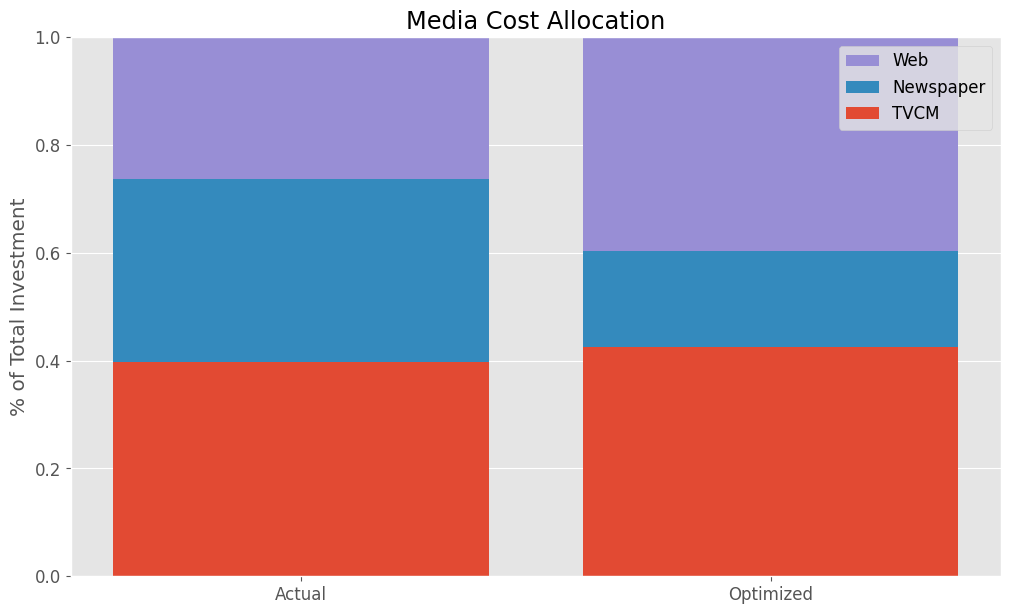
Actual Allocation Optimized Allocation TVCM 0.397076 0.425367 Newspaper 0.339156 0.178988 Web 0.263768 0.395645
パターン2:Newspaper、Webのコストを最適化
以下を最適対象の特徴量とします。
- TVCM:最適対象外
- Newspaper:最適対象の特徴量
- Web:最適対象の特徴量
以下、コードです。
# 最適化対象の特徴量のリストを作成 optimized_features = ['Newspaper', 'Web']
最適化の実行
MMMパイプラインの出力である売上を全体コスト一定(現在のコストを合計した値)のもとで最大化する、非線形最適問題を定義し、最適解を求めます。
以下、コードです。
#
# 最適投資配分
#
opt_results = optimize_investment(
trained_model,
X_actual,
optimized_features,
niter = 100)
最適化の計算が終了したら、その最適解を取得します。
以下、コードです。
# # 最適解の取得 # X_optimized = opt_results['X_optimized'] # 最適化後の特徴量を表示 print(X_optimized)
以下、実行結果です。TVCMの特徴量の値が変わっていないことが確認できます。
TVCM Newspaper Web xmas Week 2021-01-03 0 193737.291782 5.281290e+05 0 2021-01-10 0 100522.611732 1.071039e+05 0 2021-01-17 0 103844.121723 3.131483e+05 0 2021-01-24 0 219967.703139 2.730114e+05 0 2021-01-31 0 53025.161374 2.159775e+05 0 2021-02-07 0 151223.317650 2.883763e+05 0 2021-02-14 1225600 121702.363013 2.676244e+05 0 2021-02-21 1098900 89002.388308 2.326405e+05 0 2021-02-28 0 103329.489306 3.065020e+05 0 2021-03-07 0 167081.020539 1.993803e+05 0 2021-03-14 0 92782.800650 2.964036e+05 0 2021-03-21 0 138987.915440 2.459188e+05 0 2021-03-28 1274700 141903.046300 2.669003e+05 0 2021-04-04 0 144382.271078 2.485208e+05 0 2021-04-11 1302600 124429.797617 3.223905e+05 0 2021-04-18 0 121978.487582 1.625285e+05 0 2021-04-25 0 109202.350335 3.338516e+05 0 2021-05-02 0 123469.565474 2.404532e+05 0 2021-05-09 0 120346.528658 2.124192e+05 0 2021-05-16 0 134044.102973 3.087598e+05 0 2021-05-23 0 128090.803894 1.828244e+05 0 2021-05-30 0 99595.846744 3.272389e+05 0 2021-06-06 0 177339.359657 2.483121e+05 0 2021-06-13 0 85970.498869 2.674140e+05 0 2021-06-20 836300 108030.128475 2.471381e+05 0 2021-06-27 0 161894.634850 3.219619e+05 0 2021-07-04 0 85855.925771 2.112319e+05 0 2021-07-11 566400 147094.048124 2.882192e+05 0 2021-07-18 1057500 134275.376425 2.090571e+05 0 2021-07-25 0 130336.707724 3.164565e+05 0 2021-08-01 0 97680.352020 2.249677e+05 0 2021-08-08 0 137466.659338 3.300246e+05 0 2021-08-15 911700 138283.639039 1.952697e+05 0 2021-08-22 1360900 104245.491432 2.826044e+05 0 2021-08-29 734000 106210.762724 2.326234e+05 0 2021-09-05 948100 134575.802160 2.633346e+05 0 2021-09-12 0 130251.061323 2.818358e+05 0 2021-09-19 720400 86994.180486 2.397876e+05 0 2021-09-26 0 117374.931939 2.878638e+05 0 2021-10-03 0 147039.193003 2.265735e+05 0 2021-10-10 1142800 86045.990116 2.615058e+05 0 2021-10-17 0 142783.380189 2.677027e+05 0 2021-10-24 0 107207.175543 2.443140e+05 0 2021-10-31 0 133193.073082 3.081895e+05 0 2021-11-07 0 208464.936064 2.635620e+05 0 2021-11-14 0 49501.418603 2.010499e+05 0 2021-11-21 0 182770.866993 3.488196e+05 0 2021-11-28 0 140853.020028 2.136458e+05 0 2021-12-05 0 133808.490481 2.792405e+05 0 2021-12-12 0 115184.341083 1.844187e+05 0 2021-12-19 0 137271.052114 4.076124e+05 1 2021-12-26 0 27008.533109 4.163336e-15 0
最適投資配分の最適化結果の出力
現状と最適化の結果を比較していきます。
先ずは、売上金額とマーケティングROIです。
以下、コードです。
#
# 現状と最適配分時の比較(yとマーケティングROI)
#
result = compare_y_and_marketing_roi(
X_optimized,
X_actual,
y_actual,
trained_model,
apply_effects_features)
# 数値の表示
for key,value in result.items():
print(f"{key}: {value}")
以下、実行結果です。
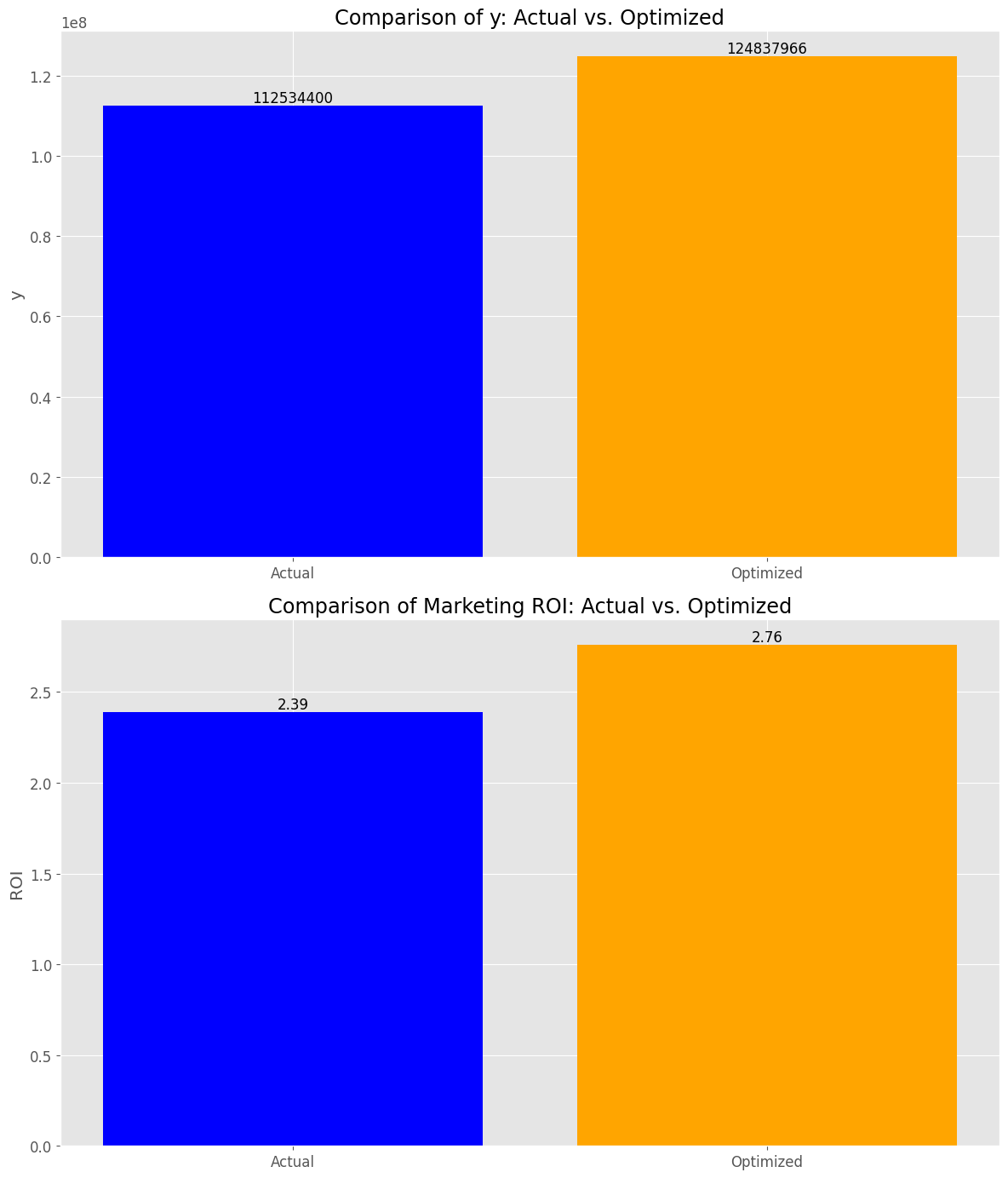
y_actual_sum: 112534400 y_optimized_sum: 124837966 y_change_percent: +10.93 % roi_actual: 2.39 roi_optimized: 2.76 roi_change_point: +0.37 points
次に、投資配分です。
以下、コードです。
#
# 投資配分構成比の比較
#
comparison_df = plot_comparative_allocation(
X_actual,
X_optimized,
apply_effects_features)
# 数値の表示
print(comparison_df)
以下、実行結果です。
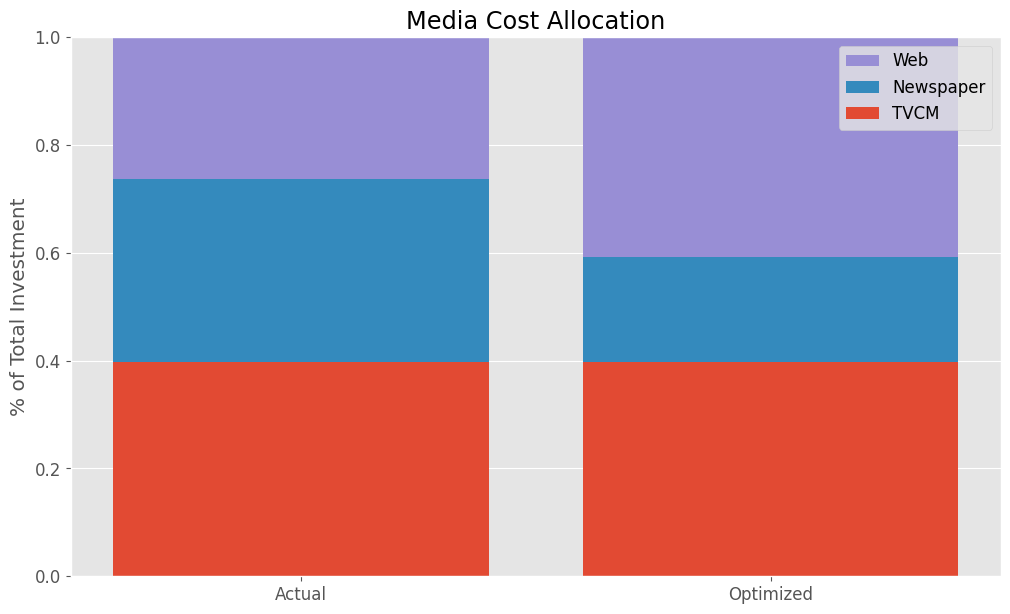
Actual Allocation Optimized Allocation TVCM 0.397076 0.397076 Newspaper 0.339156 0.195155 Web 0.263768 0.407769
TVCMの割合だけ変化していないことが分かります。
パターン3:TVCMのコストのみ最適化
以下を最適対象の特徴量とします。
- TVCM:最適対象の特徴量
- Newspaper:最適対象外
- Web:最適対象外
以下、コードです。
# 最適化対象の特徴量のリストを作成 optimized_features = ['TVCM']
最適化の実行
MMMパイプラインの出力である売上を全体コスト一定(現在のコストを合計した値)のもとで最大化する、非線形最適問題を定義し、最適解を求めます。
以下、コードです。
#
# 最適投資配分
#
opt_results = optimize_investment(
trained_model,
X_actual,
optimized_features,
niter = 100)
最適化の計算が終了したら、その最適解を取得します。
以下、コードです。
# # 最適解の取得 # X_optimized = opt_results['X_optimized'] # 最適化後の特徴量を表示 print(X_optimized)
以下、実行結果です。TVCMのみ変化しています。
TVCM Newspaper Web xmas Week 2021-01-03 2.981908e+01 0 191200 0 2021-01-10 1.496581e-13 0 212500 0 2021-01-17 1.776722e+04 0 236500 0 2021-01-24 6.650049e+01 0 201400 0 2021-01-31 4.072320e+03 420300 204400 0 2021-02-07 2.924925e+03 623800 200000 0 2021-02-14 7.873993e+05 630800 198400 0 2021-02-21 4.069887e+05 0 177900 0 2021-02-28 2.395459e+05 381500 187800 0 2021-03-07 3.533689e+05 312200 0 0 2021-03-14 2.164429e+04 451400 164000 0 2021-03-21 1.255527e+05 0 219500 0 2021-03-28 7.286935e+05 566400 234900 0 2021-04-04 2.674187e+05 622900 191100 0 2021-04-11 4.056942e+05 0 179600 0 2021-04-18 1.449231e+05 613600 167800 0 2021-04-25 2.005125e+05 0 209700 0 2021-05-02 2.506617e+05 0 187700 0 2021-05-09 5.867049e+05 0 181900 0 2021-05-16 2.382208e+05 444000 0 0 2021-05-23 3.838111e+05 482300 182900 0 2021-05-30 2.594498e+05 0 162500 0 2021-06-06 3.241907e+05 558100 224300 0 2021-06-13 1.939402e+05 628400 189700 0 2021-06-20 4.535717e+05 0 199200 0 2021-06-27 4.042932e+05 0 211400 0 2021-07-04 1.081168e+05 289800 177400 0 2021-07-11 3.183140e+05 0 182200 0 2021-07-18 4.345990e+05 0 223100 0 2021-07-25 1.577097e+04 0 185700 0 2021-08-01 4.978586e+05 383200 209500 0 2021-08-08 1.736229e+05 406100 174800 0 2021-08-15 2.327995e+05 0 0 0 2021-08-22 2.080145e+05 0 217800 0 2021-08-29 5.918010e+05 0 203300 0 2021-09-05 4.459925e+05 0 200400 0 2021-09-12 1.486660e+05 516100 157800 0 2021-09-19 2.438615e+05 0 225600 0 2021-09-26 3.224617e+05 437700 0 0 2021-10-03 7.354454e+04 0 169200 0 2021-10-10 6.161968e+05 433800 231700 0 2021-10-17 2.565280e+05 487500 190000 0 2021-10-24 1.410241e+05 0 177600 0 2021-10-31 3.845190e+05 0 175200 0 2021-11-07 3.016462e+05 0 0 0 2021-11-14 2.319192e+05 0 192800 0 2021-11-21 4.834099e+05 386300 173700 0 2021-11-28 1.406088e+05 0 0 0 2021-12-05 1.617155e+03 516700 166800 0 2021-12-12 5.561154e+03 0 206600 0 2021-12-19 1.015188e-12 664500 0 1 2021-12-26 4.735101e-14 0 197600 0
最適投資配分の最適化結果の出力
現状と最適化の結果を比較していきます。
先ずは、売上金額とマーケティングROIです。
以下、コードです。
#
# 現状と最適配分時の比較(yとマーケティングROI)
#
result = compare_y_and_marketing_roi(
X_optimized,
X_actual,
y_actual,
trained_model,
apply_effects_features)
# 数値の表示
for key,value in result.items():
print(f"{key}: {value}")
以下、実行結果です。
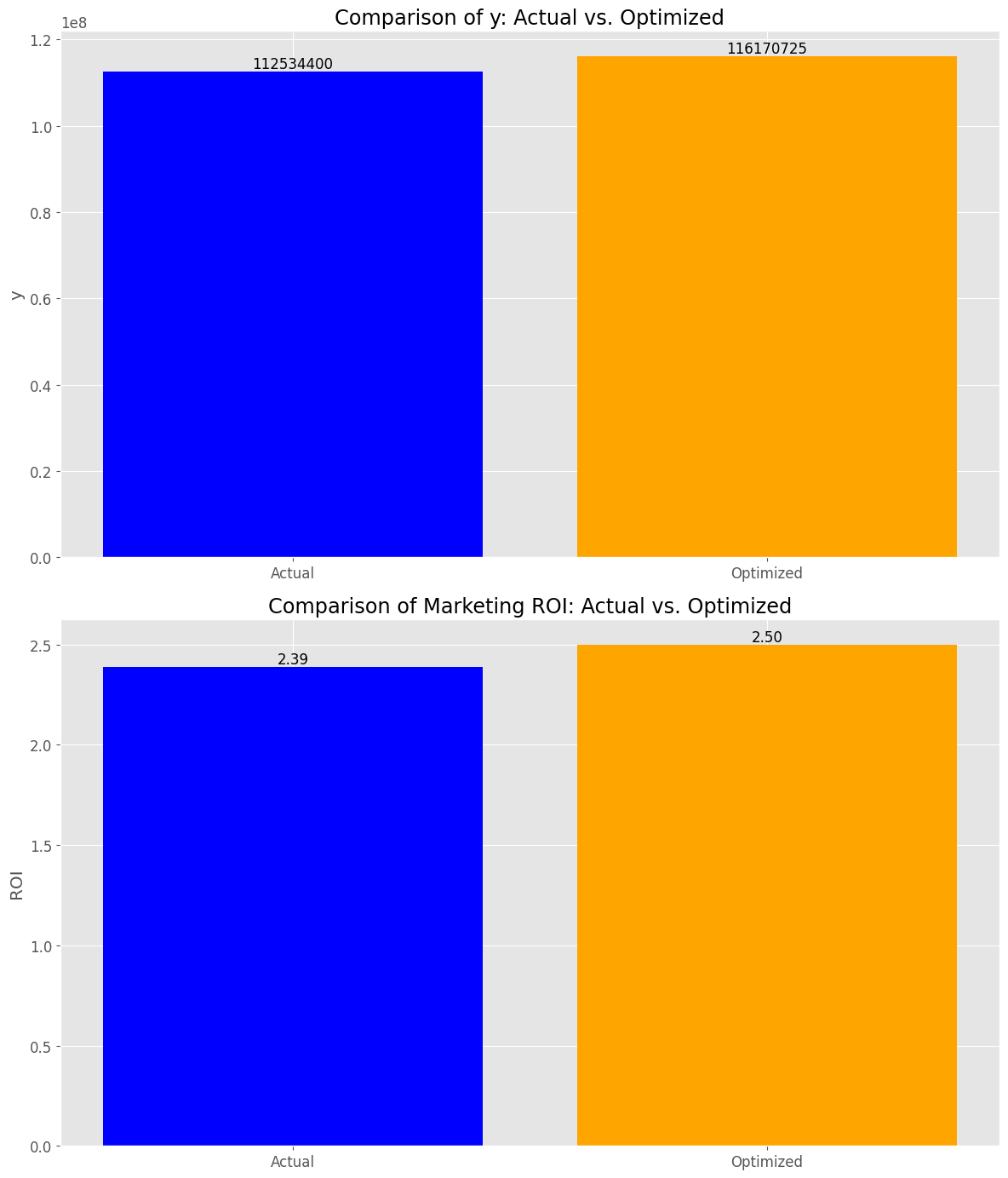
y_actual_sum: 112534400 y_optimized_sum: 116170725 y_change_percent: +3.23 % roi_actual: 2.39 roi_optimized: 2.50 roi_change_point: +0.11 points
次に、投資配分です。
以下、コードです。
#
# 投資配分構成比の比較
#
comparison_df = plot_comparative_allocation(
X_actual,
X_optimized,
apply_effects_features)
# 数値の表示
print(comparison_df)
以下、実行結果です。
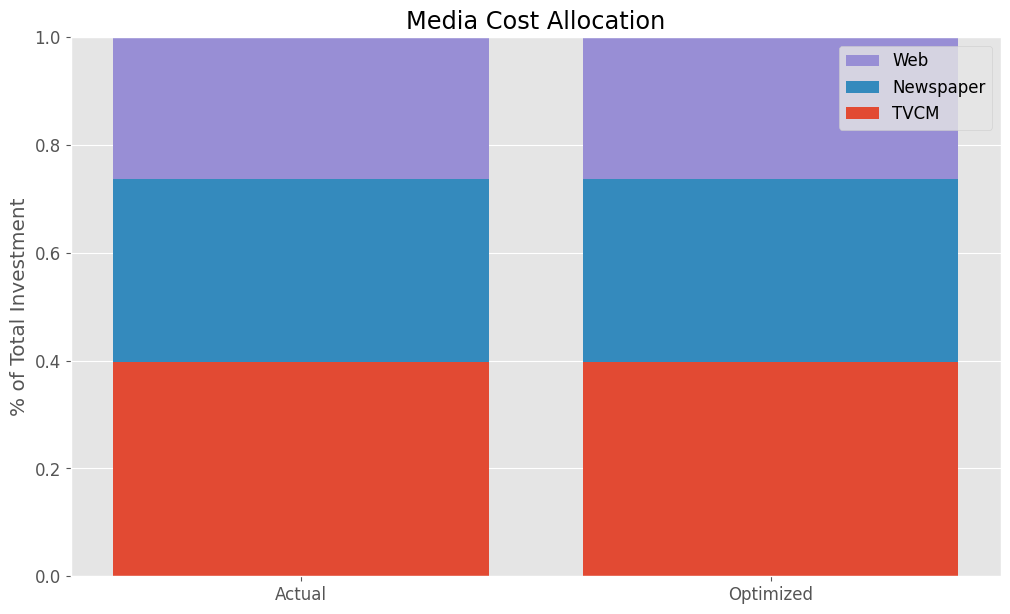
Actual Allocation Optimized Allocation TVCM 0.397076 0.397076 Newspaper 0.339156 0.339156 Web 0.263768 0.263768
集計値のため構成比に変化はありません。先ほど見た通り、TVCMの詳細を見ると異なってきます。
まとめ
今回は、「アドストックを考慮すべきどうか、コスト最適化の対象かどうか、特徴量を指定し構築する線形回帰系MMM」のお話しをしました。
ただ、アドストックのハイパーパラメータを設定する方法で、Ridge MMMパイプラインを構築したため、MMMの精度がいまいちでした。
次回は、「Ridge MMMパイプラインのハイパーパラメータをOptunaで最適化し、アドストックを考慮すべきどうか、コスト最適化の対象かどうか、特徴量を指定し構築する線形回帰系MMM」のお話しをします。
PythonによるMMM(マーケティングミックスモデリング)とビジネス活用- 振返り分析・最適投資配分編(その3)-線形回帰系MMMの最適投資配分(特徴量指定・ハイパラ自動調整)

