データを活用したマーケティング戦略は、ビジネスの成功に不可欠です。その中心に位置するのが、マーケティングミックスモデリング(MMM)です。
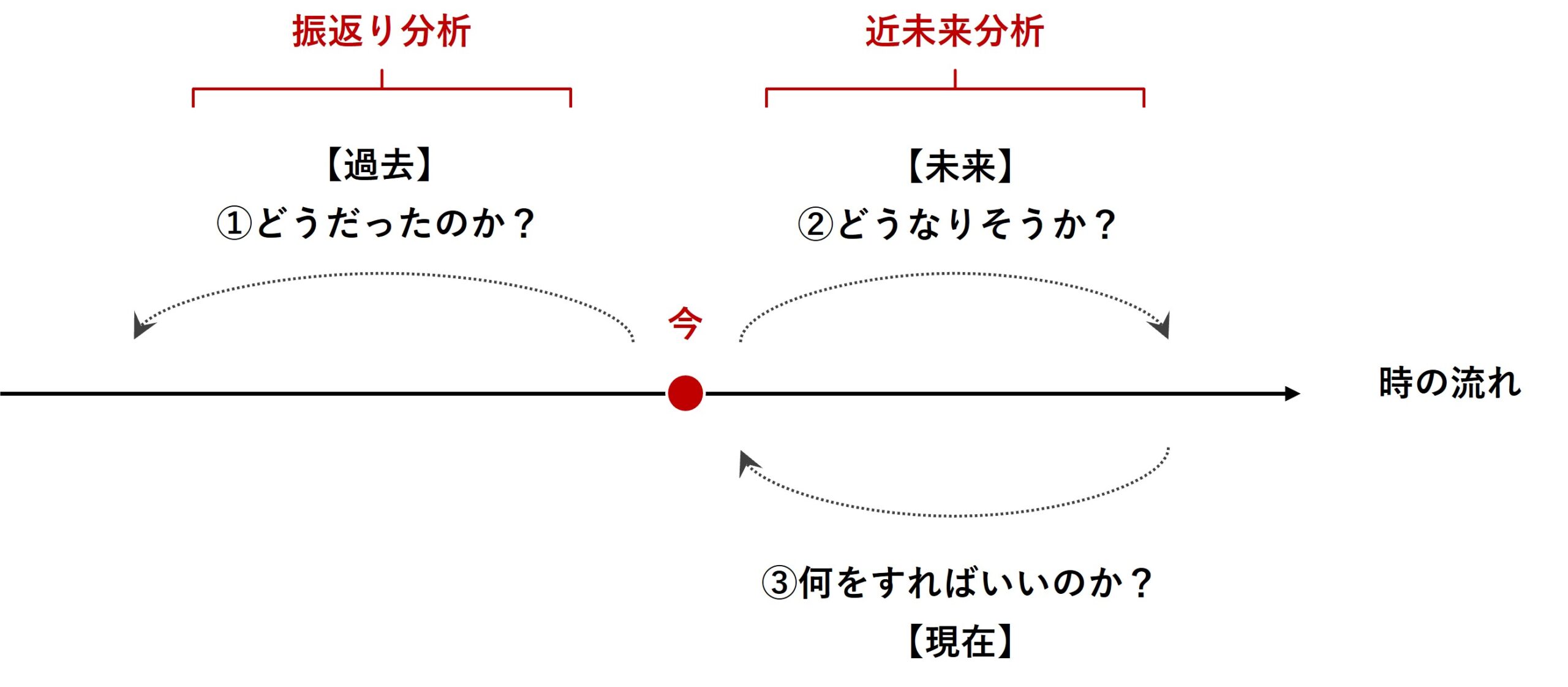
マーケティングミックスモデリング(MMM)は、過去のデータを分析する「振り返り分析」と未来のトレンドを予測する「近未来分析」の両方で有効に活用される強力なツールです。
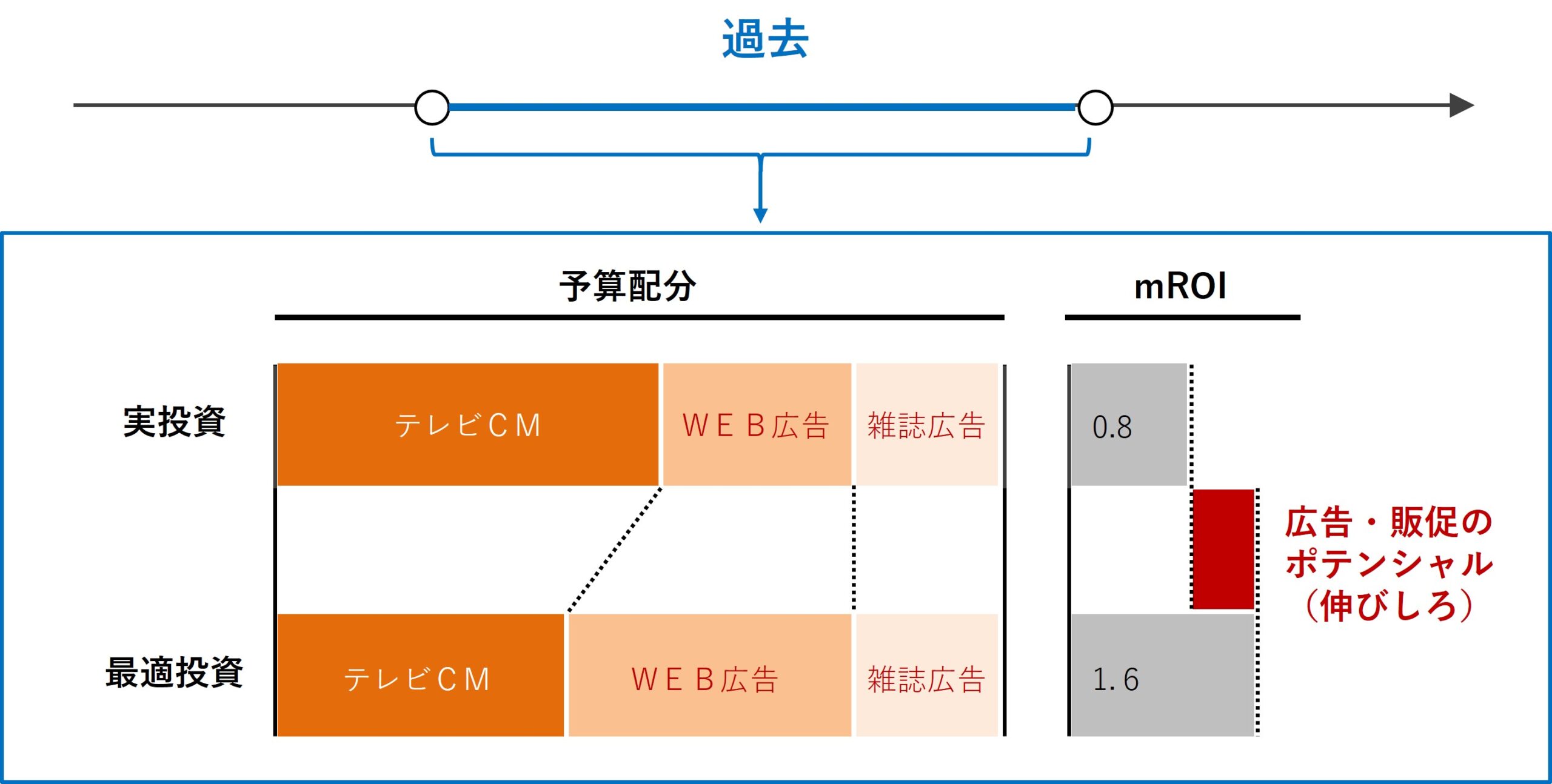
どの広告・販促の手段に、どの程度のコストをかけて投資をするのが効率的なのか? 広告・販促の手段にかけるコストの最適投資配分です。
色々なアプローチがありますが、ストレートなのは非線形計画問題(非線形最適化)を定式化しソルバーで解くことです。具体的に言うと、PythonのScyPyである程度は実現することができます。
前回は「アドストックを考慮すべきどうか、コスト最適化の対象かどうか、特徴量を指定し自動調整し構築する線形回帰系MMM」というお話しをします。
多くの時系列データには季節性があります。前回のモデルには、季節性などを考慮していませんでした。
今回は、「季節性を考慮したRidge MMMパイプラインを構築し最適投資配分を求める方法」のお話しをします。
Contents [hide]
データセットと最適投資配分
今回利用するデータセット
以下のデータセットを利用します。
- 目的変数:売上金額(Sales)
- 説明変数:
- メディア:TVCM、Newspaper、Webのコスト
- イベント:XMas(クリスマス)フラグ(1: 12月25日、0: その他)
今回利用するデータセットは、以下からダウンロードできます。
MMM_xmas.csv
https://www.salesanalytics.co.jp/dcbd
今回は、以下のように設定します。
- アドストックを考慮する:
- TVCMのコスト
- Newspaperのコスト
- Webのコスト
- アドストックを考慮しない:
- XMas(クリスマス)フラグ(1: 12月25日、0: その他)
- 季節成分(三角関数で表現)
季節成分を表現する三角関数(Sin, Cos)の特徴量は、データセットには含まれていません。データセットを読み込んだ後に、この特徴量を生成します。
今回構築するMMMと最適化
今回のMMM(マーケティングミックスモデリング)の予算最適化問題は、全体コスト一定の下で売上を最大化する、広告・販促の手段に対するコストの最適配分を求める問題になります。

MMMそのものが目的関数、MMMの出力である売上が目的変数になります。推定器にはRidge回帰を使います。
このRidge MMMパイプラインのハイパーパラメータは、Optunaで自動チューニングします。
特徴量は2つの視点で分けていきます。
- アドストックを考慮する特徴量 or そうでない特徴量
- 考慮する特徴量:TVCM、Newspaper、Webのコスト
- そうでない特徴量:XMas(クリスマス)フラグ、季節成分(三角関数で表現)
- 最適化対象となる特徴量 or そうではない特徴量
- 最適化対象となる特徴量:TVCM、Newspaper、Webのコスト
- そうではない特徴量:XMas(クリスマス)フラグ、季節成分(三角関数で表現)
今回のケースですと、アドストックを考慮すべき特徴量=最適化対象となる特徴量です。
準備
モジュールの読み込み
先ず、必要なモジュールを読み込みます。
以下、コードです。
from mmm_functions5 import *
Pythonファイル(mmm_functions5.py)そのものは、以下からダウンロードできます。
mmm_functions5.py ※zipファイルを解凍してお使いください
https://www.salesanalytics.co.jp/uno8
mmm_functions5.pyには、MMMで共通して利用する処理を関数化したものや、クラス、モジュール類などを記載しています。前回作った最適化用の関数も含まれています。
mmm_functions5.pyを利用するときは、実行するPythonファイルやNotebookと同じフォルダに入れておいてください。
上手くいかないときは、mmm_functions5.pyをメモ帳などで開き内容をコピーし、実行するPythonファイルやNotebookにコードを張り付け、Pythonで関数を作ってからMMM構築などを行ってください。
データセットの読み込み
以下、コードです。
# データセット読み込み
dataset = 'https://www.salesanalytics.co.jp/dcbd'
df = pd.read_csv(
dataset,
parse_dates=['Week'],
index_col='Week',
)
季節性を表現する特徴量を、三角関数(Sin , Cos)で生成します。
SinとCosのセットであるフーリエ項(基底)をその程度作るのかで、季節性の表現の柔軟性が変わります。多ければ多いほど柔軟な表現になります。フーリエ項(基底)の係数は、データで後で学習し求めます。
まず、フーリエ項(基底)を生成し元のデータセットに付け加える関数を定義します。
以下、コードです。
#
# 三角関数特徴量の生成関数を定義
#
def add_fourier_terms(df, num, seasonal):
'''
引数df: 元のデータフレーム
引数num: フーリエ項の数(基底の数)、sinとcosのセット数
引数seasonal: フーリエ変換の周期
戻り値: フーリエ項を追加後のデータフレーム
'''
# t列がdfにない場合、t列を0からdfの長さまでの連番で作成
if 't' not in df.columns:
df['t'] = pd.RangeIndex(start=0, stop=len(df))
# 三角関数特徴量(フーリエ項)を追加
for i in range(1, num + 1):
# sin項を追加
df['sin_' + str(i)] = np.sin(i * 2 * np.pi * df.t / seasonal)
# cos項を追加
df['cos_' + str(i)] = np.cos(i * 2 * np.pi * df.t / seasonal)
return df
この関数を使い、季節成分を生成しデータセットに加えます。
以下、コードです。
# 三角関数特徴量を追加したデータフレームを表示して確認 df = add_fourier_terms(df, num=5, seasonal=52.25) print(df) #確認
周期を52.25に設定しています。年間の週の数が52~53週間あり、多くは年間52週間ですが約4年に1度の間隔で53週になるからです。
以下、実行結果です。
Sales TVCM Newspaper Web xmas t sin_1 \
Week
2018-01-07 2132000 1312200 0 0 0 0 0.000000
2018-01-14 2596100 0 502900 237400 0 1 0.119963
2018-01-21 2236200 0 432100 200600 0 2 0.238193
2018-01-28 1680900 0 338400 0 0 3 0.352983
2018-02-04 2155400 0 0 234000 0 4 0.462674
... ... ... ... ... ... ... ...
2021-11-28 833900 0 0 0 0 203 -0.660522
2021-12-05 2064700 0 516700 166800 0 204 -0.565683
2021-12-12 1689500 0 0 206600 0 205 -0.462674
2021-12-19 3399200 0 664500 0 1 206 -0.352983
2021-12-26 1461100 0 0 197600 0 207 -0.238193
cos_1 sin_2 cos_2 sin_3 cos_3 sin_4 \
Week
2018-01-07 1.000000 0.000000 1.000000 0.000000 1.000000 0.000000
2018-01-14 0.992778 0.238193 0.971218 0.352983 0.935630 0.462674
2018-01-21 0.971218 0.462674 0.886528 0.660522 0.750806 0.820348
2018-01-28 0.935630 0.660522 0.750806 0.883026 0.469324 0.991849
2018-02-04 0.886528 0.820348 0.571865 0.991849 0.127421 0.938256
... ... ... ... ... ... ...
2021-11-28 0.750806 -0.991849 0.127421 -0.828851 -0.559470 -0.252764
2021-12-05 0.824623 -0.932951 0.360005 -0.972981 -0.230887 -0.671733
2021-12-12 0.886528 -0.820348 0.571865 -0.991849 0.127421 -0.938256
2021-12-19 0.935630 -0.660522 0.750806 -0.883026 0.469324 -0.991849
2021-12-26 0.971218 -0.462674 0.886528 -0.660522 0.750806 -0.820348
cos_4 sin_5 cos_5
Week
2018-01-07 1.000000 0.000000 1.000000
2018-01-14 0.886528 0.565683 0.824623
2018-01-21 0.571865 0.932951 0.360005
2018-01-28 0.127421 0.972981 -0.230887
2018-02-04 -0.345941 0.671733 -0.740793
... ... ... ...
2021-11-28 -0.967528 0.449297 -0.893383
2021-12-05 -0.740793 -0.134872 -0.990863
2021-12-12 -0.345941 -0.671733 -0.740793
2021-12-19 0.127421 -0.972981 -0.230887
2021-12-26 0.571865 -0.932951 0.360005
[208 rows x 16 columns]
季節成分を表現する特徴量が付け加えられているのが分かるかと思います。機能するかどうか分かりませんが、トレンド特徴量 t も追加しています。
目的変数(予測対象)と説明変数に分解します。
以下、コードです。
# 説明変数Xと目的変数yに分解 X = df.drop(columns=['Sales']) y = df['Sales']
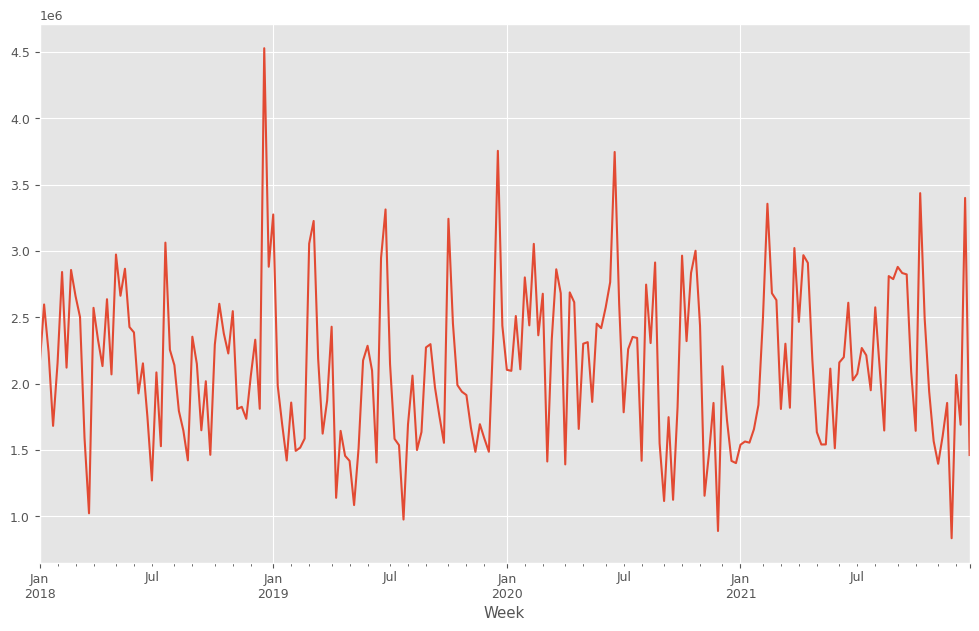
目的変数y(売上)をプロットします。
以下、コードです。
y.plot() plt.show()
以下、実行結果です。

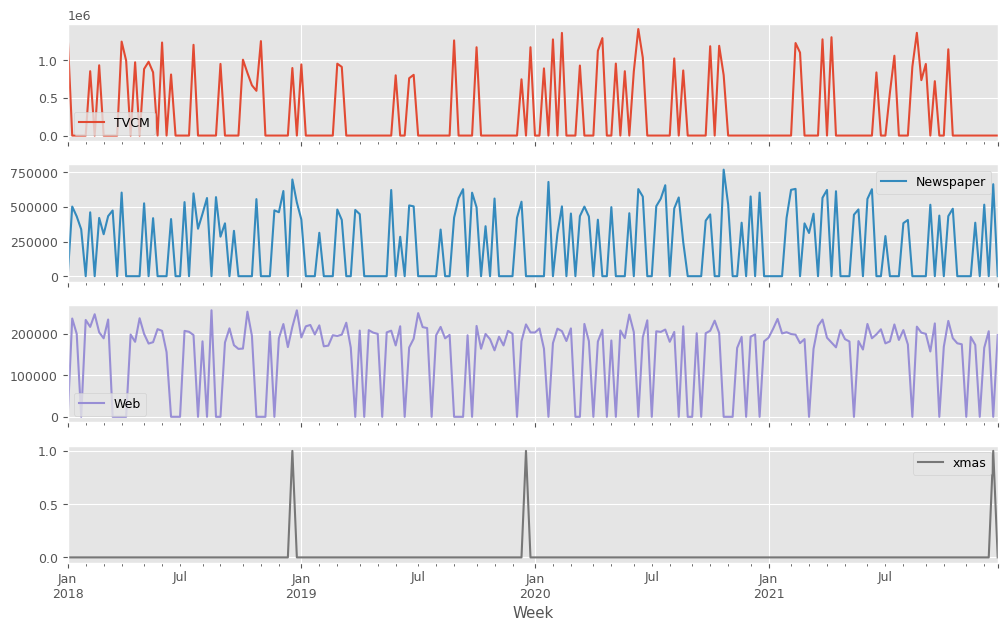
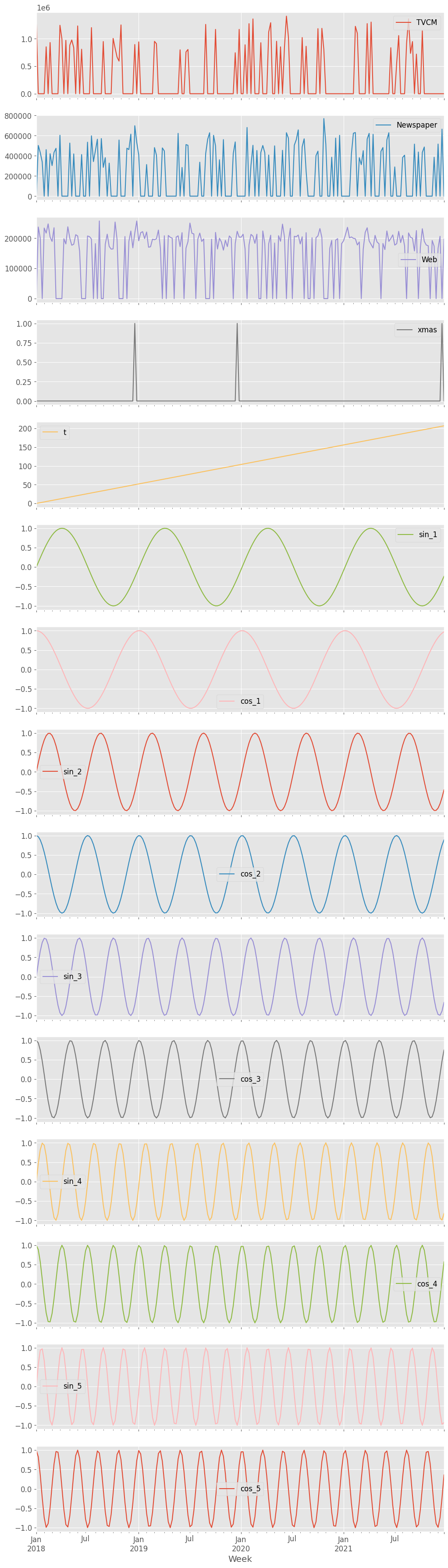
説明変数X(各メディアのコスト)をまとめてプロットします。
以下、コードです。
X.plot(subplots=True,figsize=(12,X.shape[1]*3)) plt.show()
以下、実行結果です。季節成分を表現する特徴量も表示されています。
目的関数作り
今回の最適投資配分問題の目的関数は、Ridge MMMMパイプラインそのものになります。
アドストックを考慮する特徴量のリスト
先ず、アドストックを考慮する特徴量のリストを作ります。
以下、コードです。
# アドストックを考慮する特徴量のリストを作成 apply_effects_features = ['TVCM', 'Newspaper', 'Web']
最適なハイパーパラメータの探索
Ridge MMMパイプラインのハイパーパラメータをOptunaで探索します。
先ず、Optunaの目的関数を定義します。
以下、コードです。
#
# Optunaの目的関数
#
def ridge_objective_apply_effects(trial, X, y, apply_effects_features):
carryover_params = []
curve_params = []
# 列名リストからインデックスのリストを作成
apply_effects_indices = [X.columns.get_loc(column) for column in apply_effects_features]
no_effects_indices = list(set(range(X.shape[1])) - set(apply_effects_indices))
for feature in apply_effects_features:
carryover_length = trial.suggest_int(f'carryover_length_{feature}', 1, 10)
carryover_peak = trial.suggest_int(f'carryover_peak_{feature}', 1, carryover_length)
carryover_rate1 = trial.suggest_float(f'carryover_rate1_{feature}', 0, 1)
carryover_rate2 = trial.suggest_float(f'carryover_rate2_{feature}', 0, 1)
carryover_c1 = trial.suggest_float(f'carryover_c1_{feature}', 0, 2)
carryover_c2 = trial.suggest_float(f'carryover_c2_{feature}', 0, 2)
carryover_params.append({
'length': carryover_length,
'peak': carryover_peak,
'rate1': carryover_rate1,
'rate2': carryover_rate2,
'c1': carryover_c1,
'c2': carryover_c2,
})
saturation_function = trial.suggest_categorical(f'saturation_function_{feature}', ['logistic', 'exponential'])
if saturation_function == 'logistic':
curve_param_L = trial.suggest_float(f'curve_param_L_{feature}', 0, 10)
curve_param_k = trial.suggest_float(f'curve_param_k_{feature}', 0, 10)
curve_param_x0 = trial.suggest_float(f'curve_param_x0_{feature}', 0, 2)
curve_params.append({
'saturation_function': saturation_function,
'L': curve_param_L,
'k': curve_param_k,
'x0': curve_param_x0,
})
elif saturation_function == 'exponential':
curve_param_d = trial.suggest_float(f'curve_param_d_{feature}', 0, 10)
curve_params.append({
'saturation_function': saturation_function,
'd': curve_param_d,
})
alpha = trial.suggest_float('alpha', 1e-3, 1e+3)
preprocessor = ColumnTransformer(
transformers=[
('effects', Pipeline([
('carryover', CustomCarryOverTransformer(carryover_params=carryover_params)),
('saturation', CustomSaturationTransformer(curve_params=curve_params))
]), apply_effects_indices),
('no_effects', 'passthrough', no_effects_indices)
],
remainder='drop'
)
pipeline = Pipeline(steps=[
('scaler', MinMaxScaler()),
('preprocessor', preprocessor),
('ridge', Ridge(alpha=alpha))
])
tscv = TimeSeriesSplit(n_splits=5)
scores = cross_val_score(pipeline, X, y, cv=tscv, scoring='neg_mean_squared_error')
rmse = np.mean([np.sqrt(-score) for score in scores])
return rmse
この目的関数を使い、最適なハイパーパラメータを探索する関数を定義します。
以下、コードです。
#
# Optunaによる最適なハイパーパラメータの探索実行
#
def run_optimization(objective, X, y, apply_effects_features, n_trials=1000, study=None):
# Optunaのスタディの作成と最適化の実行
if study is None:
study = optuna.create_study(direction='minimize')
objective_with_data = partial(
objective,
X=X, y=y,
apply_effects_features=apply_effects_features)
study.optimize(
objective_with_data,
n_trials=n_trials,
show_progress_bar=True)
# 最適化の実行結果の表示
print("Best trial:")
trial = study.best_trial
print(f"Value: {trial.value}")
print("Params: ")
for key, value in trial.params.items():
print(f"{key}: {value}")
return study
この関数を実行し、最適なハイパーパラメータを探索します。
以下、コードです。
study = run_optimization(
ridge_objective_apply_effects,
X, y,
apply_effects_features,
n_trials=5000)
以下、実行結果です。
Best trial: 4938. Best value: 237010: 100%|██████████| 5000/5000 [52:42<00:00, 1.58it/s]Best trial: Value: 237010.09434071128 Params: carryover_length_TVCM: 5 carryover_peak_TVCM: 1 carryover_rate1_TVCM: 0.9729271018598733 carryover_rate2_TVCM: 0.2966298925357188 carryover_c1_TVCM: 1.2314141219113544 carryover_c2_TVCM: 0.546825967722917 saturation_function_TVCM: exponential curve_param_d_TVCM: 1.9183272984812656 carryover_length_Newspaper: 2 carryover_peak_Newspaper: 1 carryover_rate1_Newspaper: 0.17197042046525332 carryover_rate2_Newspaper: 0.43965062701472585 carryover_c1_Newspaper: 1.0338752928967323 carryover_c2_Newspaper: 0.13346846589535857 saturation_function_Newspaper: exponential curve_param_d_Newspaper: 1.6739264306006938 carryover_length_Web: 7 carryover_peak_Web: 1 carryover_rate1_Web: 0.5503030669166483 carryover_rate2_Web: 0.19277860756776197 carryover_c1_Web: 1.3333660220153671 carryover_c2_Web: 1.751549177057382 saturation_function_Web: logistic curve_param_L_Web: 1.674062430952774 curve_param_k_Web: 2.8891224711920658 curve_param_x0_Web: 0.3463030631752817 alpha: 0.08860413121661548
MMMパイプラインの構築
Optunaで探索し見つけたハイパーパラメータを取得し、Ridge MMMパイプラインを構築します。
そのための関数を定義します。
以下、コードです。
def create_model_from_trial_ridge(trial, X, y, apply_effects_features):
#
# Optunaの実行結果からハイパーパラメータを取得
#
carryover_keys = ['length', 'peak', 'rate1', 'rate2', 'c1', 'c2']
curve_keys_logistic = ['L', 'k', 'x0']
curve_keys_exponential = ['d']
# ハイパーパラメータを抽出しキーと値の辞書を作成
def fetch_params(prefix, feature_name, params, trial_params):
return {key: trial_params[f'{prefix}_{key}_{feature_name}'] for key in params}
# キャリーオーバー効果関数ハイパーパラメータを抽出
carryover_params = [fetch_params('carryover', feature_name, carryover_keys, trial.params) for feature_name in apply_effects_features]
# 飽和関数ハイパーパラメータを抽出
curve_params = []
for feature_name in apply_effects_features:
saturation_function = trial.params[f'saturation_function_{feature_name}']
curve_param = {'saturation_function': saturation_function}
if saturation_function == 'logistic':
curve_param.update(fetch_params('curve_param', feature_name, curve_keys_logistic, trial.params))
elif saturation_function == 'exponential':
curve_param.update(fetch_params('curve_param', feature_name, curve_keys_exponential, trial.params))
curve_params.append(curve_param)
# 推定器ハイパーパラメータを抽出
alpha = trial.params['alpha']
#
# MMMパイプラインの構築&学習
#
MMM_pipeline, trained_model, pred = build_MMM_pipeline_ridge(
X, y,
apply_effects_features,
carryover_params,
curve_params,
alpha)
# 最適ハイパーパラメータの集約
model_params = [
carryover_params,
curve_params,
alpha]
return trained_model,model_params
戻り値のtrained_modelが学習済みのRidge MMMパイプラインで、model_paramsがそのハイパーパラメータです。
では、この関数を実行します。
以下、コードです。
trained_model,model_params = create_model_from_trial_ridge(
study.best_trial,
X, y,
apply_effects_features)
以下、実行結果です。
RMSE: 177802.61978860805 MAE: 145419.2861950865 MAPE: 0.07475479898495105 R2: 0.9116853811170141
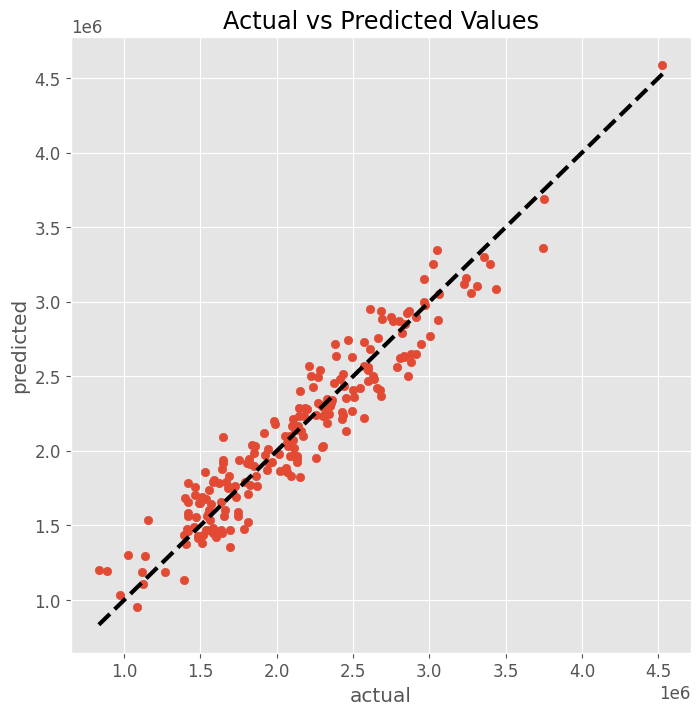
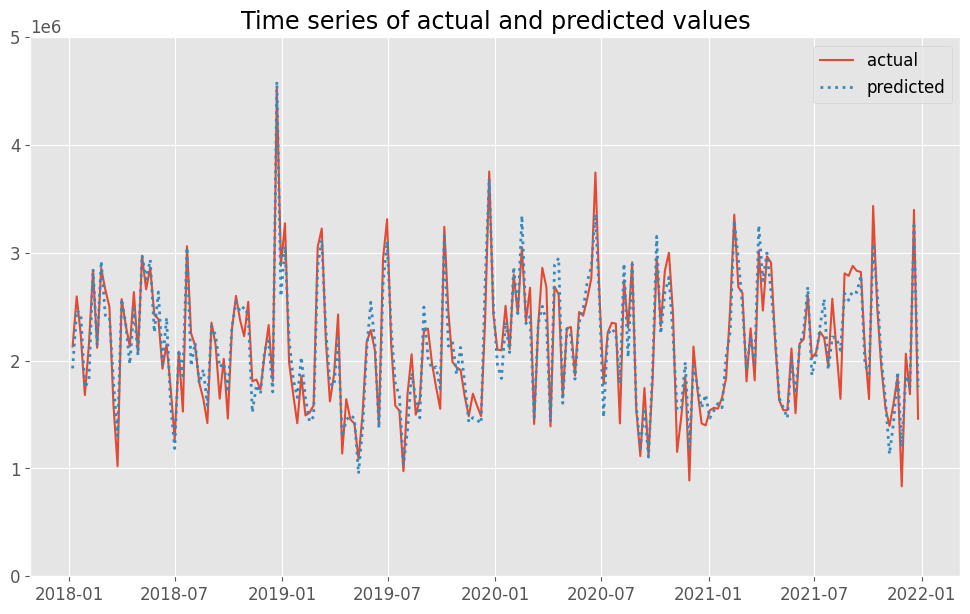
アドストックの状況をグラフで確認します。
以下、コードです。
# グラフで確認
best_carryover_params = model_params[0]
best_curve_params = model_params[1]
plot_effects(
best_carryover_params,
best_curve_params,
apply_effects_features)
以下、実行結果です。
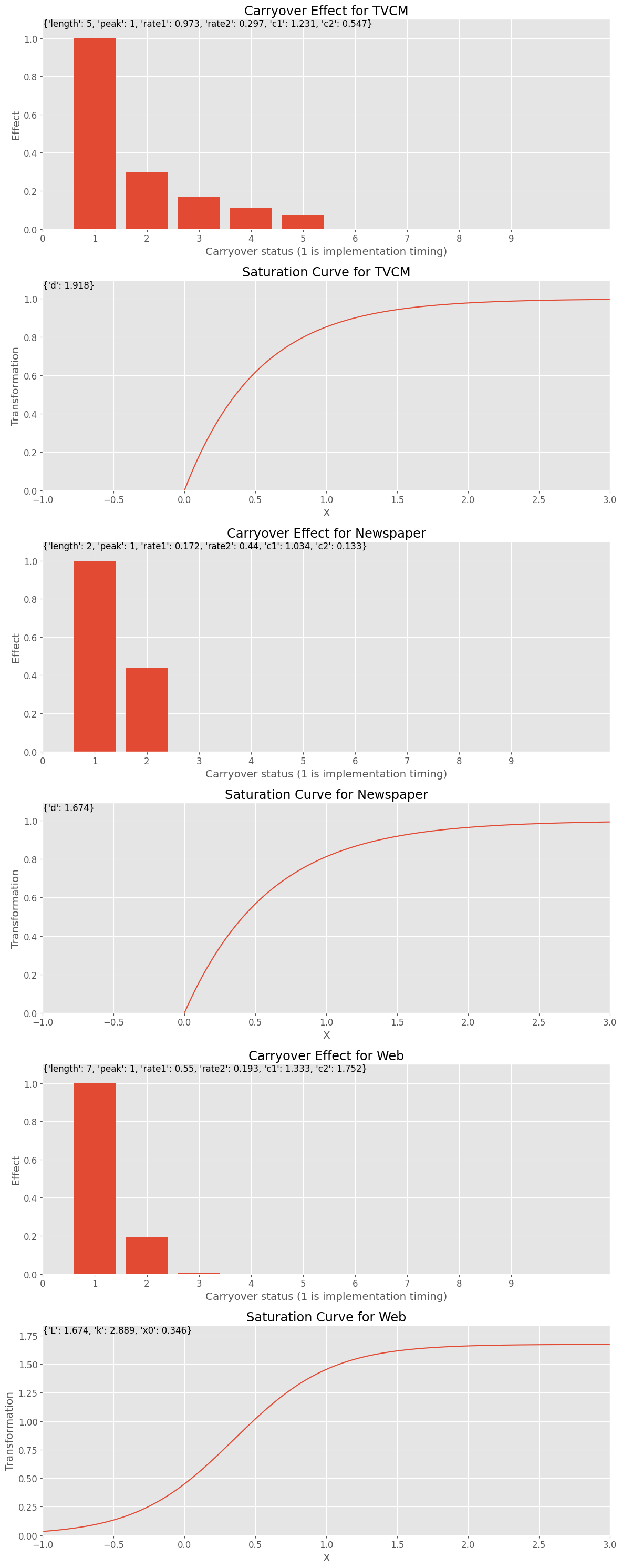
売上貢献度とマーケティングROI
このMMMパイプラインから、売上貢献度やマーケティングROIなどを求めていきます。
先ずは、貢献度の推移です。
以下、関数です。
# 貢献度の算出
def calculate_and_plot_contribution(y, X, model, ylim=None, apply_effects_features=None):
"""
各媒体の売上貢献度を算定し、結果をプロットする関数。
:param y: ターゲット変数
:param X: 特徴量のデータフレーム
:param model: 学習済みモデル
:param ylim: y軸の表示範囲
:return: 各媒体の貢献度
"""
if apply_effects_features is None:
apply_effects_features = X.columns
# yの予測
pred = model.predict(X)
pred = pd.DataFrame(pred, index=X.index, columns=['y'])
# 値がすべて0の説明変数
X_ = X.copy()
X_[apply_effects_features] = 0
# Baseの予測
base = model.predict(X_)
pred['Base'] = base
# 各媒体の予測
for feature in apply_effects_features:
X_[apply_effects_features] = 0
X_[feature] = X[feature]
pred[feature] = model.predict(X_) - base
# 予測値の補正
correction_factor = y.div(pred.y, axis=0)
pred_adj = pred.mul(correction_factor, axis=0)
contribution = pred_adj.drop(columns=['y'])
# apply_effects_features以外をbaseに集約
contribution['Base'] = contribution.drop(columns=apply_effects_features).sum(axis=1)
contribution = contribution[['Base'] + list(apply_effects_features)]
# エリアプロット
if ylim is not None:
ax = contribution.plot.area()
handles, labels = ax.get_legend_handles_labels()
ax.legend(reversed(handles), reversed(labels))
ax.set_ylim(ylim)
plt.title('Contributions over time')
plt.show()
return contribution
この関数を使います。
以下、コードです。
# 貢献度の算出
contribution = calculate_and_plot_contribution(
y, X,
trained_model, (0, 5e6),
apply_effects_features)
# 数値を表示
print(contribution)
以下、実行結果です。
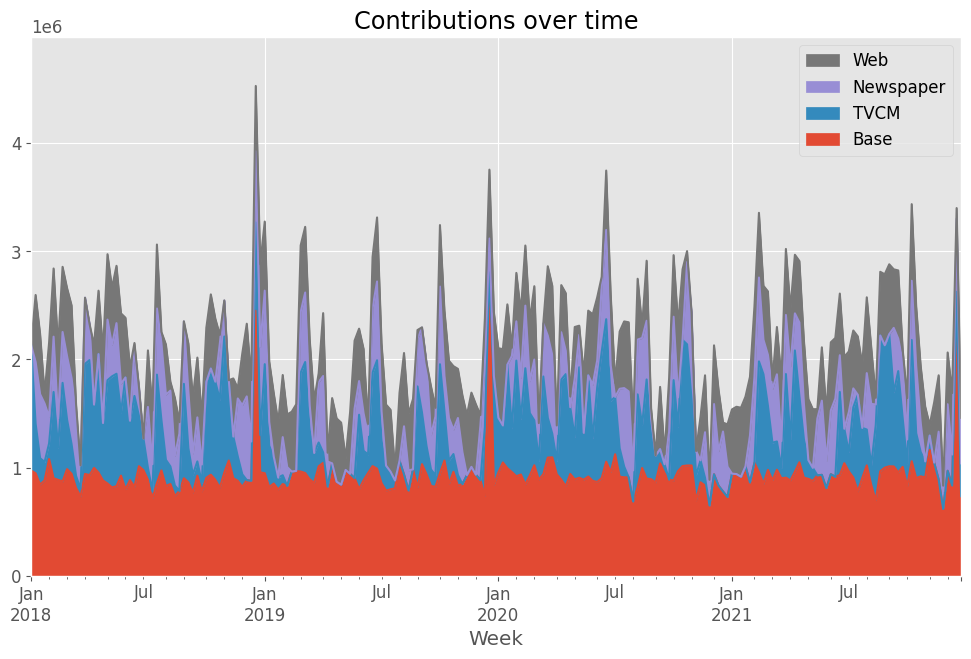
Base TVCM Newspaper Web Week 2018-01-07 9.733873e+05 1.158613e+06 0.000000 0.000000 2018-01-14 9.484278e+05 4.575676e+05 572240.872421 617863.665059 2018-01-21 8.437181e+05 2.446132e+05 590972.178279 556896.546019 2018-01-28 8.832017e+05 1.694063e+05 540022.457974 88269.537959 2018-02-04 1.079710e+06 1.453228e+05 242901.141448 687466.000783 ... ... ... ... ... 2021-11-28 6.187977e+05 0.000000e+00 160501.533787 54600.793797 2021-12-05 9.717705e+05 0.000000e+00 614667.094955 478262.412278 2021-12-12 8.355731e+05 0.000000e+00 285893.821197 568033.124942 2021-12-19 2.624556e+06 0.000000e+00 676402.630602 98241.655198 2021-12-26 7.368754e+05 0.000000e+00 303580.715522 420643.921625 [208 rows x 4 columns]
次に、貢献度の構成比を求めます。
以下、コードです。
# 貢献度構成比の算出 contribution_results = summarize_and_plot_contribution(contribution) print(contribution_results)
以下、実行結果です。
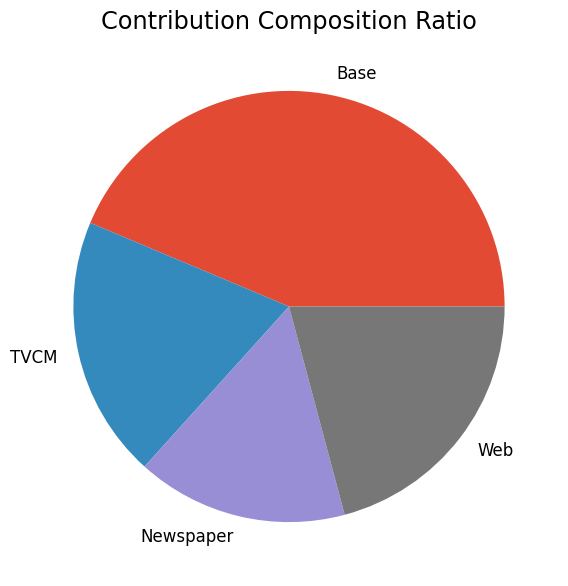
contribution ratio Base 1.939308e+08 0.436588 TVCM 8.731737e+07 0.196574 Newspaper 7.037395e+07 0.158430 Web 9.257458e+07 0.208409
売上貢献度とコストから、マーケティングROIを求めます。
以下、コードです。
# マーケティングROIの算出
ROI = calculate_marketing_roi(
X[apply_effects_features],
contribution[apply_effects_features]
)
# 数値を表示
print(ROI)
以下、実行結果です。
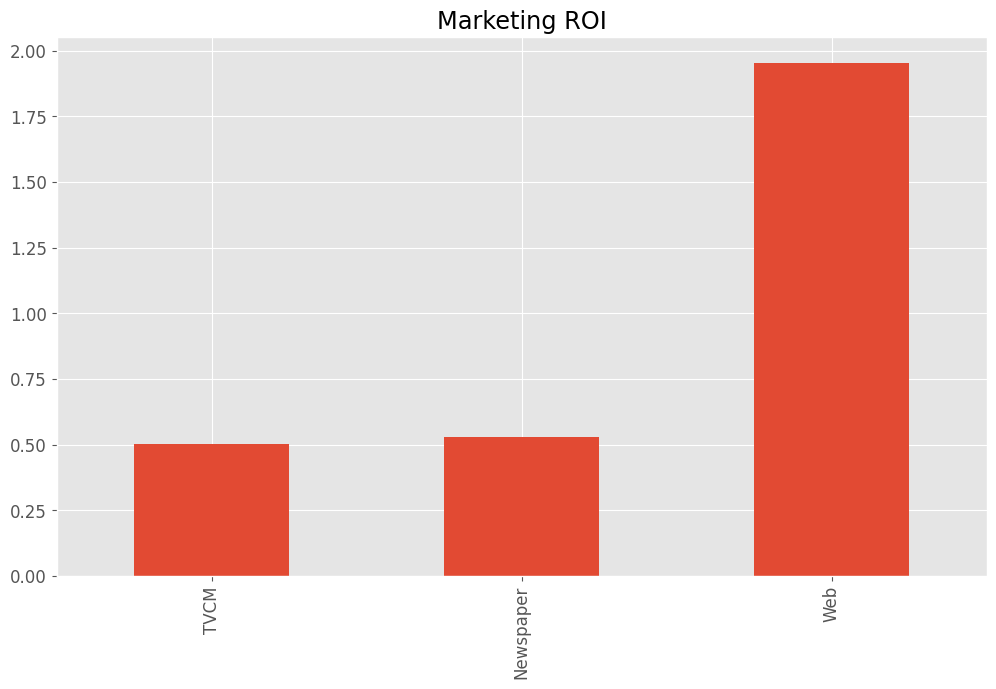
TVCM 0.501653 Newspaper 0.530328 Web 1.954888 dtype: float64
売上貢献度(横軸)×マーケティングROI(縦軸)のマップを描きます。円の大きさはコストを表します。
以下、コードです。
# 散布図作成(売上貢献度×マーケティングROI)
data_to_plot = plot_scatter_of_contribution_and_roi(
X[apply_effects_features],
contribution[apply_effects_features]
)
# 散布図の数値を表示
print(data_to_plot)
以下、実行結果です。
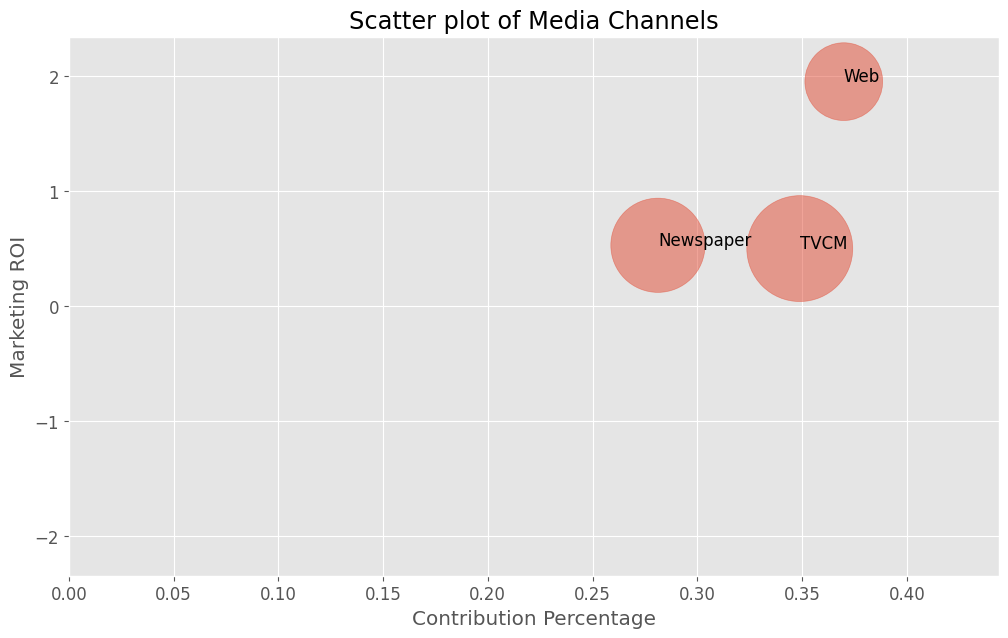
contribution_percentage ROI cost TVCM 0.348898 0.501653 58147500 Newspaper 0.281197 0.530328 45986200 Web 0.369905 1.954888 31329300
最適投資配分
構築したRidge MMMMパイプラインを最大化する最適投資配分問題を解き、広告・販促のコストの最適投資配分を求めます。
最後に、現状と最適化後の結果を比較し、どのような変化が起こるかを出力します。
最適化する期間の設定
最適化する期間は、直近1年間(52週間)です。
以下、コードです。
# 最適化期間を表す変数、ここでは直近1年間(52週間)を指定 term = 52 # 最適化期間における対象特徴量Xのデータを抽出 X_actual = X[-term:] # 最適化期間における目的変数yのデータを抽出 y_actual = y[-term:]
最適化対象となる特徴量のリストを作ります。
以下、コードです。
# 最適化対象の特徴量のリストを作成 optimized_features = ['TVCM', 'Newspaper', 'Web']
最適化の実行
MMMパイプラインの出力である売上を全体コスト一定(現在のコストを合計した値)のもとで最大化する、非線形最適問題を定義し、最適解を求めます。
以下、コードです。
#
# 最適投資配分
#
opt_results = optimize_investment(
trained_model,
X_actual,
optimized_features,
niter = 100)
最適化の計算が終了したら、その最適解を取得します。
以下、コードです。
# # 最適解の取得 # X_optimized = opt_results['X_optimized'] # 最適化後の特徴量を表示 print(X_optimized)
以下、実行結果です。
TVCM Newspaper Web xmas t sin_1 \
Week
2021-01-03 2.061352e+05 2.644306e+05 310760.065241 0 156 -0.090067
2021-01-10 2.820323e+05 1.117502e+05 230997.697922 0 157 0.030059
2021-01-17 2.949620e+05 2.160800e+05 242852.249510 0 158 0.149750
2021-01-24 3.444725e+05 1.516047e+05 245585.117776 0 159 0.267279
2021-01-31 1.351958e+05 1.238194e+05 265601.756952 0 160 0.380947
2021-02-07 1.343701e+05 2.116608e+05 248820.252306 0 161 0.489113
2021-02-14 1.107157e+05 1.326450e+05 243661.017964 0 162 0.590215
2021-02-21 2.390946e+05 1.204536e+05 274648.400151 0 163 0.682792
2021-02-28 3.677431e+05 1.253575e+05 254981.515806 0 164 0.765507
2021-03-07 1.968231e+05 1.785299e+05 225062.292553 0 165 0.837166
2021-03-14 1.750784e+05 3.667548e+04 236888.864095 0 166 0.896734
2021-03-21 2.848373e+05 2.094940e+05 242672.624940 0 167 0.943350
2021-03-28 1.183038e+05 1.570854e+05 256401.391217 0 168 0.976341
2021-04-04 2.465790e+05 1.830803e+05 245122.335734 0 169 0.995231
2021-04-11 3.441379e+05 1.410329e+05 250977.997496 0 170 0.999746
2021-04-18 2.160167e+05 2.380970e+05 274478.956773 0 171 0.989821
2021-04-25 9.369076e+04 5.558819e+04 227047.171968 0 172 0.965601
2021-05-02 2.576445e+05 2.332610e+05 256482.973451 0 173 0.927434
2021-05-09 2.763834e+05 2.945121e+04 245927.612613 0 174 0.875872
2021-05-16 2.750688e+05 2.015922e+05 275373.440519 0 175 0.811659
2021-05-23 2.728347e+05 2.553521e+05 248861.686229 0 176 0.735724
2021-05-30 2.784224e+05 1.308278e+05 249622.778472 0 177 0.649162
2021-06-06 2.546980e+05 1.921193e+05 248196.469036 0 178 0.553225
2021-06-13 2.297822e+05 3.544338e+04 260218.581156 0 179 0.449297
2021-06-20 9.609488e+04 2.627430e+05 246502.612645 0 180 0.338879
2021-06-27 3.356055e+05 1.732794e+05 246117.691204 0 181 0.223568
2021-07-04 9.761630e+04 1.026479e+05 250492.129535 0 182 0.105027
2021-07-11 3.944771e+05 1.773457e+05 270486.425030 0 183 -0.015031
2021-07-18 1.046504e+05 1.469566e+05 260655.360809 0 184 -0.134872
2021-07-25 1.920452e+05 1.764217e+05 250140.277433 0 185 -0.252764
2021-08-01 1.129333e+05 1.051399e+05 250111.803128 0 186 -0.367006
2021-08-08 1.134429e+05 1.729849e+05 244519.653023 0 187 -0.475947
2021-08-15 3.832926e+05 2.737565e+05 256552.331685 0 188 -0.578014
2021-08-22 2.467442e+05 1.093583e+05 263957.792264 0 189 -0.671733
2021-08-29 1.026868e+05 1.371510e+05 258313.865490 0 190 -0.755750
2021-09-05 3.275985e+05 3.043407e+05 255756.315131 0 191 -0.828851
2021-09-12 2.076493e+05 2.153542e+05 269322.250659 0 192 -0.889981
2021-09-19 2.487868e+05 1.538675e+05 247410.733366 0 193 -0.938256
2021-09-26 1.573702e+05 1.152559e+05 256671.594054 0 194 -0.972981
2021-10-03 1.274701e+05 2.426804e+05 258019.369393 0 195 -0.993652
2021-10-10 3.443403e+05 1.301170e+05 251272.048838 0 196 -0.999972
2021-10-17 2.602334e+05 1.024540e+05 252699.894656 0 197 -0.991849
2021-10-24 1.848510e+05 1.417980e+05 260098.047352 0 198 -0.969400
2021-10-31 3.031779e+05 2.406517e+05 244038.726161 0 199 -0.932951
2021-11-07 9.548359e+04 1.855220e+05 252773.081327 0 200 -0.883026
2021-11-14 3.483452e+05 2.466583e+05 264883.660641 0 201 -0.820348
2021-11-21 1.709500e+05 1.139804e+05 270617.597124 0 202 -0.745821
2021-11-28 4.228808e+05 2.833392e+05 228132.460122 0 203 -0.660522
2021-12-05 1.072361e+05 1.840752e+05 217757.755691 0 204 -0.565683
2021-12-12 3.004597e+05 1.681535e+05 301859.071554 0 205 -0.462674
2021-12-19 9.516851e+03 2.258705e+05 220780.378198 1 206 -0.352983
2021-12-26 1.018596e-16 3.008496e-09 222917.397170 0 207 -0.238193
cos_1 sin_2 cos_2 sin_3 cos_3 sin_4 \
Week
2021-01-03 0.995936 -0.179402 0.983776 -0.267279 0.963619 -0.352983
2021-01-10 0.999548 0.060090 0.998193 0.090067 0.995936 0.119963
2021-01-17 0.988724 0.296123 0.955150 0.435817 0.900035 0.565683
2021-01-24 0.963619 0.515110 0.857124 0.725461 0.688264 0.883026
2021-01-31 0.924597 0.704445 0.709759 0.921708 0.387885 0.999972
2021-02-07 0.872220 0.853229 0.521537 0.999294 0.037570 0.889981
2021-02-14 0.807246 0.952897 0.303293 0.948231 -0.317582 0.578014
2021-02-21 0.730613 0.997713 0.067590 0.775092 -0.631848 0.134872
2021-02-28 0.643427 0.985096 -0.172003 0.502168 -0.864770 -0.338879
2021-03-07 0.546948 0.915773 -0.401695 0.164595 -0.986361 -0.735724
2021-03-14 0.442570 0.793734 -0.608264 -0.194169 -0.980968 -0.965601
2021-03-21 0.331799 0.626005 -0.779819 -0.527935 -0.849285 -0.976341
2021-03-28 0.216236 0.422240 -0.906484 -0.793734 -0.608264 -0.765507
2021-04-04 0.097550 0.194169 -0.980968 -0.957348 -0.288936 -0.380947
2021-04-11 -0.022545 -0.045079 -0.998983 -0.997713 0.067590 0.090067
2021-04-18 -0.142315 -0.281733 -0.959493 -0.909632 0.415415 0.540641
2021-04-25 -0.260029 -0.502168 -0.864770 -0.704445 0.709759 0.868520
2021-05-02 -0.373987 -0.693697 -0.720267 -0.408567 0.912728 0.999294
2021-05-09 -0.482544 -0.845293 -0.534303 -0.060090 0.998193 0.903285
2021-05-16 -0.584131 -0.948231 -0.317582 0.296123 0.955150 0.602282
2021-05-23 -0.677282 -0.996584 -0.082579 0.614213 0.789141 0.164595
2021-05-30 -0.760650 -0.987570 0.157177 0.853229 0.521537 -0.310446
2021-06-06 -0.833032 -0.921708 0.387885 0.982400 0.186791 -0.715033
2021-06-13 -0.893383 -0.802788 0.596265 0.985096 -0.172003 -0.957348
2021-06-20 -0.940830 -0.637656 0.770322 0.860971 -0.508653 -0.982400
2021-06-27 -0.974688 -0.435817 0.900035 0.626005 -0.779819 -0.784502
2021-07-04 -0.994469 -0.208892 0.977939 0.310446 -0.950591 -0.408567
2021-07-11 -0.999887 0.030059 0.999548 -0.045079 -0.998983 0.060090
2021-07-18 -0.990863 0.267279 0.963619 -0.394801 -0.918766 0.515110
2021-07-25 -0.967528 0.489113 0.872220 -0.693697 -0.720267 0.853229
2021-08-01 -0.930218 0.682792 0.730613 -0.903285 -0.429041 0.997713
2021-08-08 -0.879474 0.837166 0.546948 -0.996584 -0.082579 0.915773
2021-08-15 -0.816027 0.943350 0.331799 -0.961583 0.274513 0.626005
2021-08-22 -0.740793 0.995231 0.097550 -0.802788 0.596265 0.194169
2021-08-29 -0.654861 0.989821 -0.142315 -0.540641 0.841254 -0.281733
2021-09-05 -0.559470 0.927434 -0.373987 -0.208892 0.977939 -0.693697
2021-09-12 -0.455998 0.811659 -0.584131 0.149750 0.988724 -0.948231
2021-09-19 -0.345941 0.649162 -0.760650 0.489113 0.872220 -0.987570
2021-09-26 -0.230887 0.449297 -0.893383 0.765507 0.643427 -0.802788
2021-10-03 -0.112498 0.223568 -0.974688 0.943350 0.331799 -0.435817
2021-10-10 0.007516 -0.015031 -0.999887 0.999746 -0.022545 0.030059
2021-10-17 0.127421 -0.252764 -0.967528 0.927434 -0.373987 0.489113
2021-10-24 0.245485 -0.475947 -0.879474 0.735724 -0.677282 0.837166
2021-10-31 0.360005 -0.671733 -0.740793 0.449297 -0.893383 0.995231
2021-11-07 0.469324 -0.828851 -0.559470 0.105027 -0.994469 0.927434
2021-11-14 0.571865 -0.938256 -0.345941 -0.252764 -0.967528 0.649162
2021-11-21 0.666146 -0.993652 -0.112498 -0.578014 -0.816027 0.223568
2021-11-28 0.750806 -0.991849 0.127421 -0.828851 -0.559470 -0.252764
2021-12-05 0.824623 -0.932951 0.360005 -0.972981 -0.230887 -0.671733
2021-12-12 0.886528 -0.820348 0.571865 -0.991849 0.127421 -0.938256
2021-12-19 0.935630 -0.660522 0.750806 -0.883026 0.469324 -0.991849
2021-12-26 0.971218 -0.462674 0.886528 -0.660522 0.750806 -0.820348
cos_4 sin_5 cos_5
Week
2021-01-03 0.935630 -0.435817 0.900035
2021-01-10 0.992778 0.149750 0.988724
2021-01-17 0.824623 0.682792 0.730613
2021-01-24 0.469324 0.976341 0.216236
2021-01-31 0.007516 0.927434 -0.373987
2021-02-07 -0.455998 0.553225 -0.833032
2021-02-14 -0.816027 -0.015031 -0.999887
2021-02-21 -0.990863 -0.578014 -0.816027
2021-02-28 -0.940830 -0.938256 -0.345941
2021-03-07 -0.677282 -0.969400 0.245485
2021-03-14 -0.260029 -0.660522 0.750806
2021-03-21 0.216236 -0.119963 0.992778
2021-03-28 0.643427 0.462674 0.886528
2021-04-04 0.924597 0.883026 0.469324
2021-04-11 0.995936 0.993652 -0.112498
2021-04-18 0.841254 0.755750 -0.654861
2021-04-25 0.495655 0.252764 -0.967528
2021-05-02 0.037570 -0.338879 -0.940830
2021-05-09 -0.429041 -0.811659 -0.584131
2021-05-16 -0.798284 -0.999746 -0.022545
2021-05-23 -0.986361 -0.837166 0.546948
2021-05-30 -0.950591 -0.380947 0.924597
2021-06-06 -0.699090 0.208892 0.977939
2021-06-13 -0.288936 0.725461 0.688264
2021-06-20 0.186791 0.987570 0.157177
2021-06-27 0.620126 0.903285 -0.429041
2021-07-04 0.912728 0.502168 -0.864770
2021-07-11 0.998193 -0.075087 -0.997177
2021-07-18 0.857124 -0.626005 -0.779819
2021-07-25 0.521537 -0.957348 -0.288936
2021-08-01 0.067590 -0.952897 0.303293
2021-08-08 -0.401695 -0.614213 0.789141
2021-08-15 -0.779819 -0.060090 0.998193
2021-08-22 -0.980968 0.515110 0.857124
2021-08-29 -0.959493 0.909632 0.415415
2021-09-05 -0.720267 0.985096 -0.172003
2021-09-12 -0.317582 0.715033 -0.699090
2021-09-19 0.157177 0.194169 -0.980968
2021-09-26 0.596265 -0.394801 -0.918766
2021-10-03 0.900035 -0.845293 -0.534303
2021-10-10 0.999548 -0.999294 0.037570
2021-10-17 0.872220 -0.802788 0.596265
2021-10-24 0.546948 -0.324699 0.945817
2021-10-31 0.097550 0.267279 0.963619
2021-11-07 -0.373987 0.765507 0.643427
2021-11-14 -0.760650 0.995231 0.097550
2021-11-21 -0.974688 0.875872 -0.482544
2021-11-28 -0.967528 0.449297 -0.893383
2021-12-05 -0.740793 -0.134872 -0.990863
2021-12-12 -0.345941 -0.671733 -0.740793
2021-12-19 0.127421 -0.972981 -0.230887
2021-12-26 0.571865 -0.932951 0.360005
最適投資配分の最適化結果の出力
現状と最適化の結果を比較していきます。
先ずは、売上金額とマーケティングROIです。
以下、コードです。
#
# 現状と最適配分時の比較(yとマーケティングROI)
#
result = compare_y_and_marketing_roi(
X_optimized,
X_actual,
y_actual,
trained_model,
apply_effects_features)
# 数値の表示
for key,value in result.items():
print(f"{key}: {value}")
以下、実行結果です。
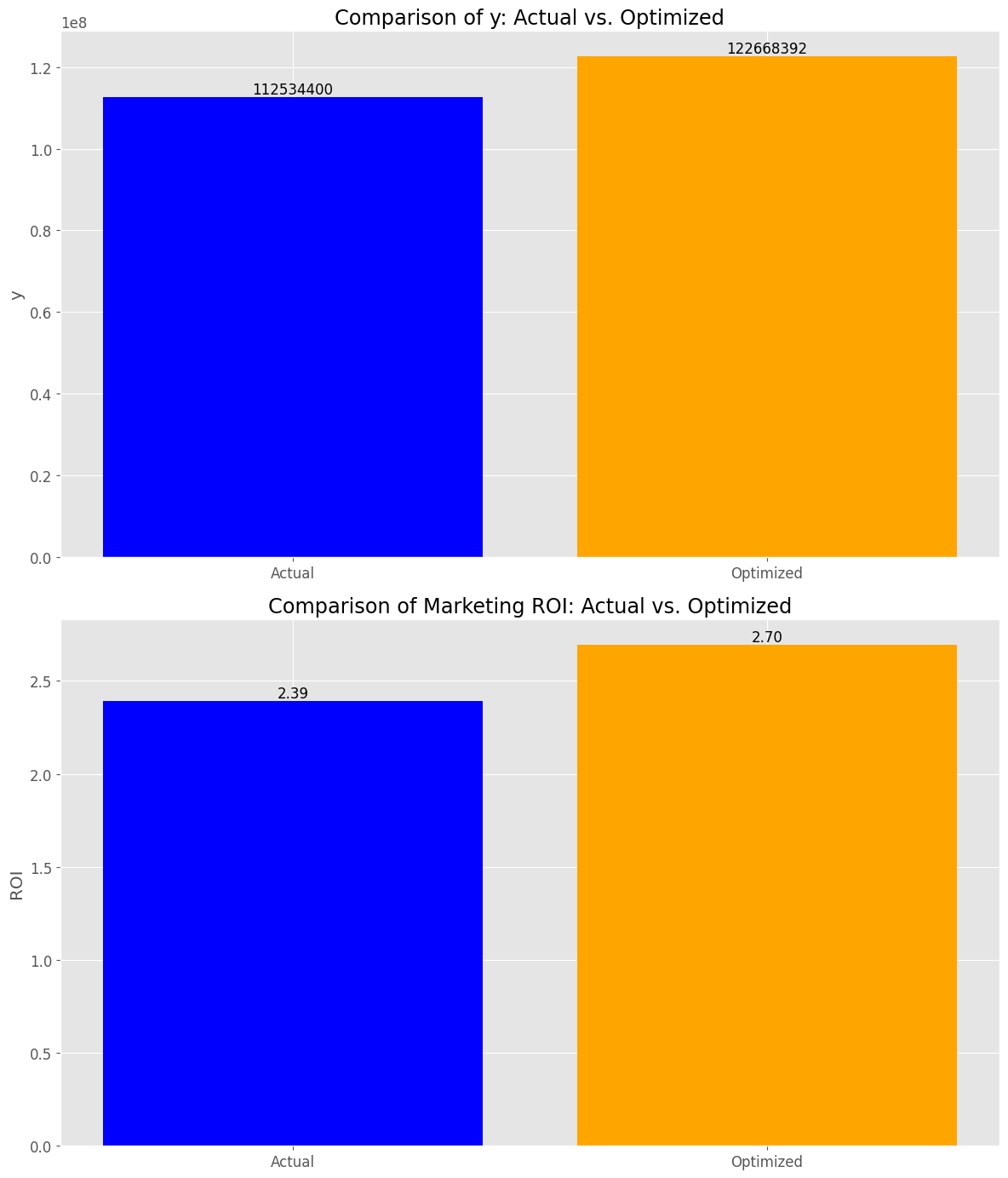
y_actual_sum: 112534400 y_optimized_sum: 122668392 y_change_percent: +9.01 % roi_actual: 2.39 roi_optimized: 2.70 roi_change_point: +0.31 points
次に、投資配分です。
以下、コードです。
#
# 投資配分構成比の比較
#
comparison_df = plot_comparative_allocation(
X_actual,
X_optimized,
apply_effects_features)
# 数値の表示
print(comparison_df)
以下、実行結果です。
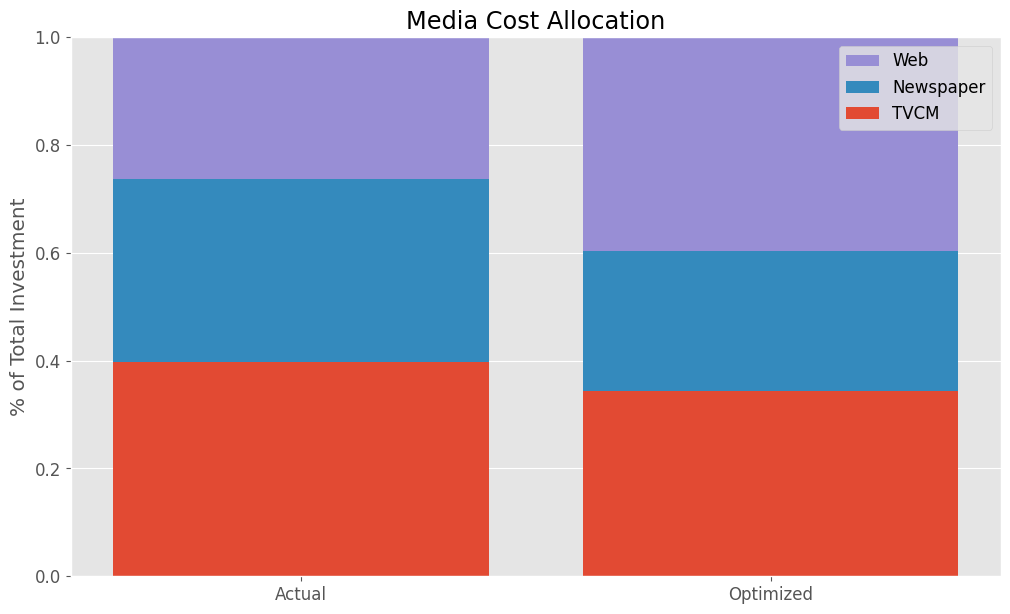
Actual Allocation Optimized Allocation TVCM 0.397076 0.344385 Newspaper 0.339156 0.259919 Web 0.263768 0.395696
まとめ
今回は、「季節性を考慮したRidge MMMパイプラインを構築し最適投資配分を求める方法」のお話しをしました。
ただ季節性は、広告の効果にも影響を及ぼすことでしょう。たとえば、同じ広告コストを投下しても、時期によって売上を伸ばす力が異なるということです。
幾つかやり方があります。
その1つが、季節変数と広告変数の交互作用をモデルに組み込むという方法です。
次回は、その交互作用項を組み込んだRidge MMMパイプラインを構築し最適投資配分を求める方法のお話しをしました。

